三极管

2020-02-09 fishedee 后端

1 概述

做单片机开发中，总是离不开三极管。只是在原来我看的那本《模拟与数字电子电路基础》中涉及不多，所以就需要加料了

2 结构

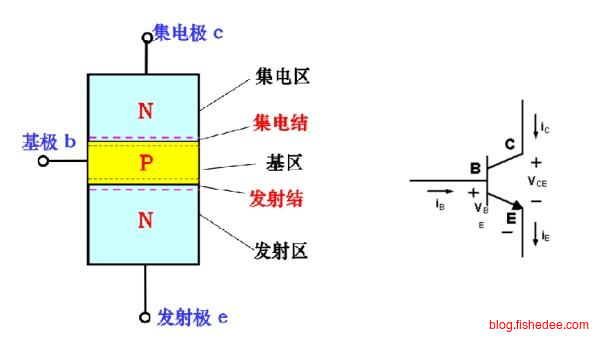
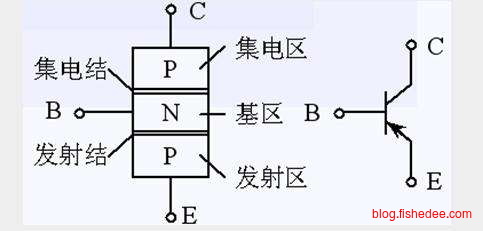
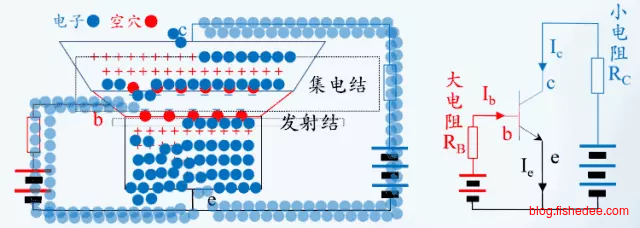
三极管，这是一个和MOSFET类似的开关结构。分为基极B，集电极C，和发射极E。三极管可以分为NPN型和PNP型，类似于MOSFET的NMOS，和PMOS的区别。无论是PNP型，还是NPN型，电流总是从P走向N。

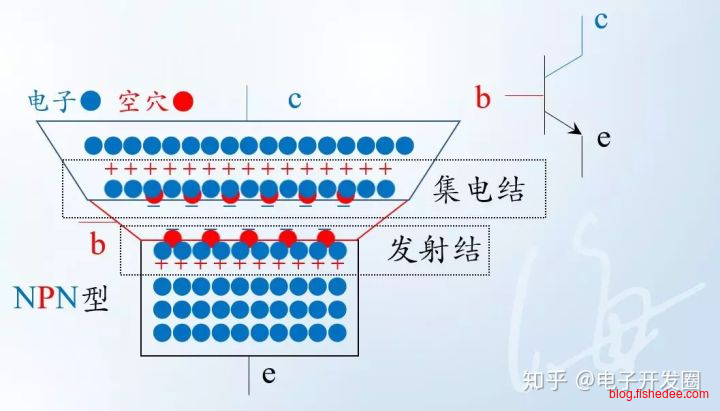
以NPN三极管为例，中间的基极很薄，充满了空穴，发射区的电子从发射区无法运动到集电区。

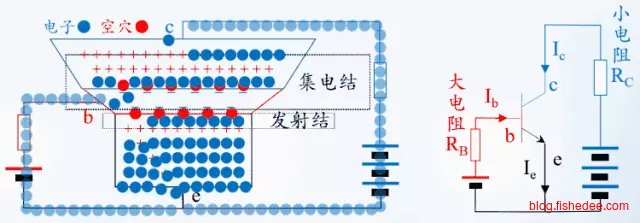
当基极-发射极正偏时，少量的电子就能从发射区沿着薄薄的基区，运到到基极。而另外一方面，更多的电子会从基区漂移到集电区，这样就形成了发射极，和集极的电流了。

当基极-发射极的电压变大时，更多的电子就能从发射区沿着薄薄的基区，运到到基极。而相应的，更多的电子能更容易从基区漂移到集电区，这样发射极和集极的电流就能更大了。

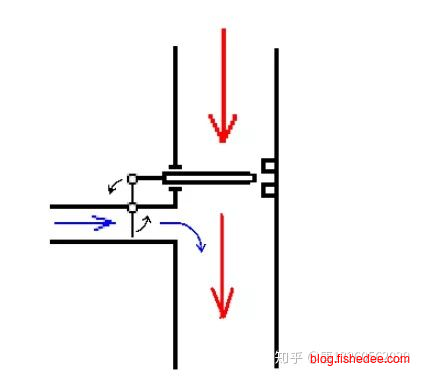
从分析中可以看出，be的电流相当于一个开关，它的电流越大，ce之间的电流阀门的开关就能更大，ce之间流过的电流就能更大。

3 模型

\[ i_{cmax}=\beta i_b \]

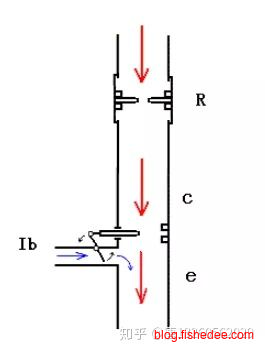
设\(i_b\)为基极电流，\(i_{cmax}\)为发射极电流，因此，我们能得到以上的模型来拟合NPN的运作，这个\(\beta\)一般为100。基极的电流就像一个阀门控制着发射极最大能允许通过的电流。注意，是最大能允许通过的电流，而不是实际流过的电流。

例如，假设\(i_c\)为之前含有一个大电阻\(R\)，那么即使\(i_b\)再大，也不可能让\(i_c>\frac {V_C} {R}\)。

另外，be之间有一个导通电压\(v_{TH}\)，只有\(v_{be}>v_{TH}\)时，\(i_b\)才能有电流通过，否则就认为\(i_b=0\)，一旦导通了以后，\(v_{be}\)的电压差为固定值\(v_{TH}\)，该\(v_{TH}\)一般为\(0.7V\)。

那么，在导通的情况下，\(v_{ce}\)之间的电压就很难说了。因为

\[ i_b = \frac {v_{ss}-v_{TH}}{R_B}\\ i_c = \begin{cases} 0,i_b=0\\ \beta i_b,i_b>0且\beta i_b < \frac {V_{cc}}{R_c}\\ \frac {V_{cc}} {R_c},i_b>0且\beta i_b >= \frac {V_{cc}}{R_c}\\ \end{cases}\\ v_{ce} = V_{cc}-i_cR_c \]

我们求得了在各种情况下关于\(i_c\)和\(v_{ce}\)的方程。我们从方程中可以看出，当\(i_c\)为第三种情况下，\(v_{ce}\)固定为\(0V\)，但是，当\(i_c\)为第二种情况下,\(v_{ce}=V_{cc}-\beta i_b R_c\)就不是一个固定值了，它是一个关于\(i_b\)的方程，这个数值可大可小。

\[ i_c = \begin{cases} 0,i_b=0\\ \beta i_b,i_b>0且\beta i_b < \frac {V_{cc}-0.2V}{R_c}\\ \frac {V_{cc}-0.2V} {R_c},i_b>0且\beta i_b >= \frac {V_{cc}-0.2V}{R_c}\\ \end{cases}\\ v_{ce} = V_{cc}-i_cR_c \]

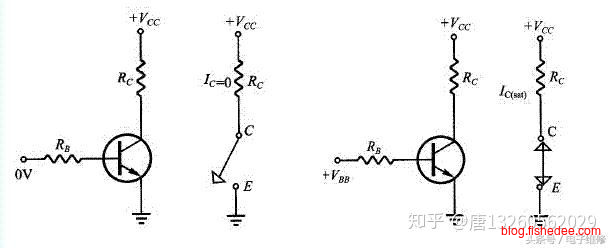
而在实际的三极管情况下，\(v_{ce}\)的最小导通电压降为0.2V，而不是0V，所以，在严格情况下的方程应该为上式。另外，我们称第一种情况为三极管的截止状态，第二种情况为三极管的放大状态，第三种情况称为三极管的饱和状态。再次强调的是，无论是在放大状态，还是在饱和状态，三极管的\(v_{be}\)在导通的情况下就是固定的。

4 应用

4.1 开关电路

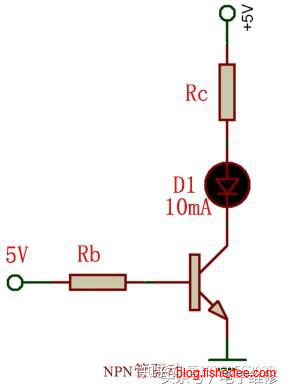
三极管一般可用作TTL逻辑门电路，以及负载增强电路。这个时候，我们都用到了三极管的饱和区域，称为三极管的开关电路。例如，我们要让发光二极管工作，它的工作电流为10mA，但是假设我们单片机的IO门最大只能输出1mA的电流，所以，我们用三极管来达到增强负载能力的目的。

\[ V_c = 5V-1V-0.2V = 3.8V\\ R_c = \frac {V_c} {I_c} = \frac {3.8V} {10mA} = 380\Omega \]

首先，我们求出需要和发光二极管串联的电阻\(R_c\)的阻值应该为\(380\Omega\)，其中发光二极管的压降固定为1V，三极管在饱和状态的压降为0.2V。

\[ i_b = \frac {i_c} {\beta} = \frac {10mA} {50} = 200\mu A\\ R_b = \frac {5V-0.7V} {i_b} = \frac {4.3V}{200\mu A} =22k\Omega \]

然后，假设三极管的放大倍数为50倍，固定的\(v_{be}\)导通压降为0.7V，因此\(R_b\)的阻值最大为\(22k\Omega\)。当然，\(R_b\)可以更小一点，这样在三极管的最大通过电流\(i_{cmax}\)能更大一点，保证了二极管在最大的发光状态。但是，\(R_b\)不能太少，因为过大的电流通过基极—发射极，会很有可能烧掉三极管。

假设，我们让\(R_b\)的电阻上升到\(33k\Omega\)，那么会造成：

\[ i_b = \frac {5V-0.7V}{33k\Omega} = 130\mu A\\ i_c = \beta i_b = 50*130\mu A = 6.5mA\\ v_ce = 5V-1V-i_c R_c = 4V-6.5mA*380\Omega = 1.53V\\ \]

二极管的电流过低，无法充分点亮，并且三极管工作在放大区域，它的发射极-集极电压不是为0.2V，而是1.53V。

4.2 放大电路

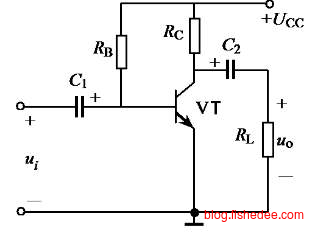
三极管也可以用作信号放大电路，稳压电路。这个时候，我们都用到了三极管的放大区域。例如，上图是一个共发射极的放大电路。\(u_0\)的输出受到\(U_{cc}\)和\(u_i\)的两个电压源的影响，在线性电路中，我们可以使用叠加原理。\(U_{cc}\)电压源的单独激励加上\(u_i\)电压源的单独激励，就是总的激励。一般称\(U_{cc}\)为偏置电路，\(u_i\)为信号输入电路。

\[ \because i_{cmax} < \frac {U_{cc}}{R_C}\\ i_{cmax} < i_{cemax}\\ \therefore R_C > \frac {U_{cc}} {i_{cemax}} \]

首先，确定\(R_c\)电阻，三极管工作在放大区域的时候，要保证电阻不会成为\(i_{c}\)的瓶颈，同时又要保证，三极管的\(i_{c}\)不能太大，不然会烧坏三极管。有了这些关系后，我们就能求出\(R_C\)的下限。

\[ \beta i_b < \frac {U_{cc}}{R_C}\\ i_b = \frac {U_{cc}-0.7V}{R_B}\\ \beta \frac {U_{cc}-0.7V}{R_B}< \frac {U_{cc}}{R_C}\\ R_B > \beta \frac {(U_{cc}-0.7V)R_C}{U_{cc}} \]

因此，有了\(R_B\)以后，我们也能求得\(R_b\)的下限。

\[ u_o = U_{cc} - \beta \frac {Ucc-0.7V} {R_B}R_C \]

最后，我们在确定了\(R_C\)和\(R_B\)的范围后，就能保证三极管总是能在三极管区域运行后，我们就能求得输入与输出的关系为上式。可以看出，输出是反相的。另外\(C_1\)和\(C_2\)是滤波电容的，它的功能是过滤掉输入和输出的直流部分，只通过输入和输出的交流部分。

相关文章