6 数字抽象
6.1 静态原则
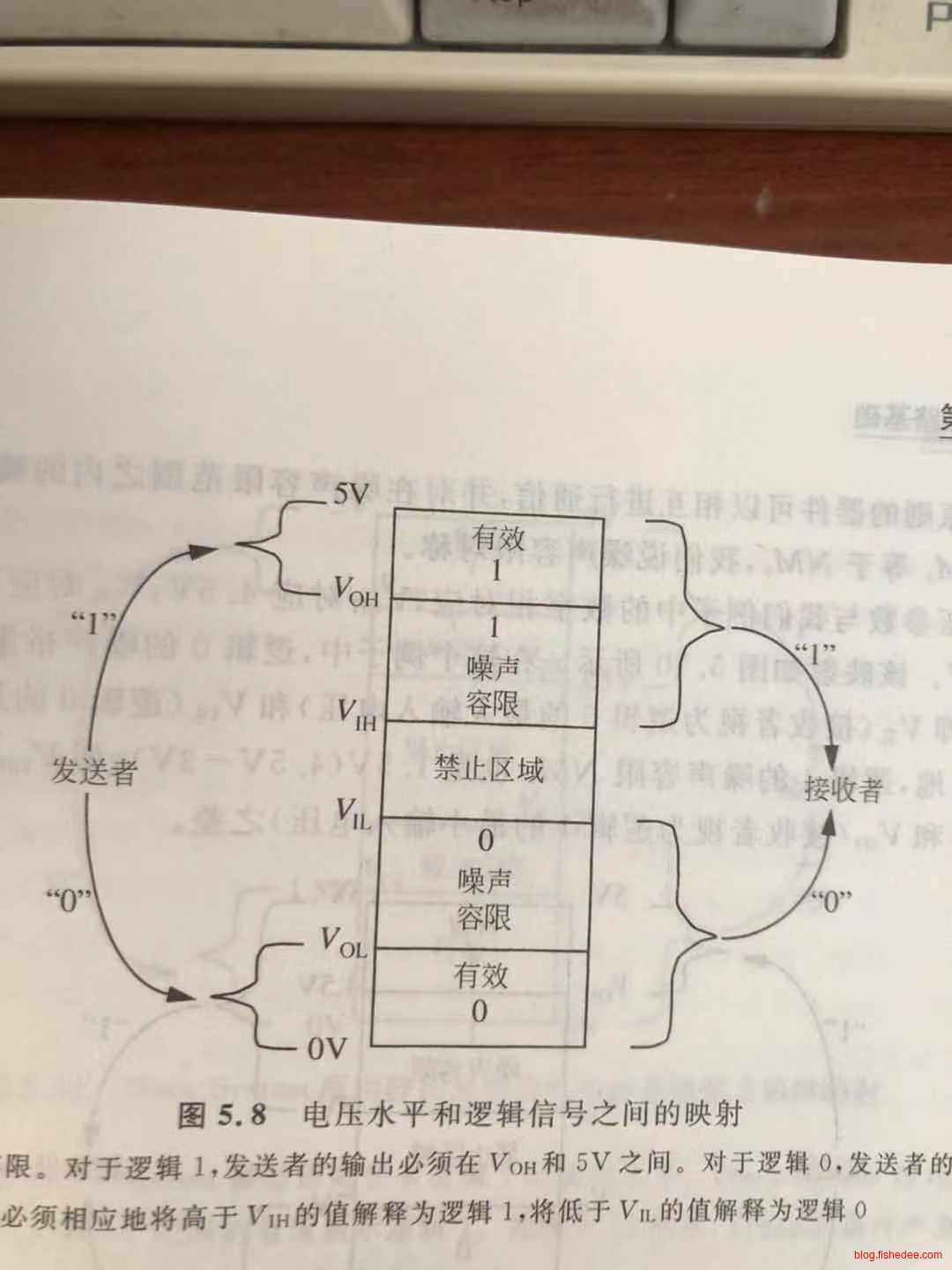
噪声容限,对于给定逻辑值,指定的输出电压和相应的接受者禁止区域电压阀值之差的绝对值称为该逻辑值的噪声容限。
静态原则,静态原则是数字器件的规范。静态原则要求器件能够正确地解释输入阀值(\(V_{IL}\)和\(V_{IH}\))规定范围内的电压。如果为器件提供了有效输入,该原则还要求器件能够产生满足输出阀值(\(V_{OL}\)和\(V_{OH}\))要求的有效输出电压。
6.2 布尔逻辑
| 算子 | 符号 |
|---|---|
| AND | * |
| OR | + |
| NOT | ~ |
6.3 组合门
一个组合门是满足下列两个特性的电路的抽象表示:
- 它的输出仅为输入的函数
- 它满足静态原则
6.4 标准乘积之和
乘积之和,用乘积之和形式的逻辑表达采用两级操作。首先是一系列乘积项(AND),每项包含真值形式的变量(如\(A\)),或补值形式的变量(\(\overline{A}\)),然后用OR逻辑将其组合起来。
6.5 简化逻辑表达
基本规则:
\[ A\cdot \overline{A} = 0\\ A \cdot A = A\\ A \cdot 0 = 0\\ A \cdot 1 = A\\ A + \overline{A} = 1\\ A + A = A\\ A + 0 = A\\ A + 1 = 1\\ A + \overline{A}B = A +B ,这个重点\\ A(B+C) = AB + AC\\ AB= BA\\ A + B = B + A\\ (AB)C = A(BC)\\ (A+B)+C = A+(B+C)\\ \]
De Mogran定理:
\[ \overline{A \cdot B} = \overline{A}+\overline{B}\\ \overline{A+B} = \overline{A}\cdot \overline{B} \]
7 MOSFET开关
7.1 MOSFET元件
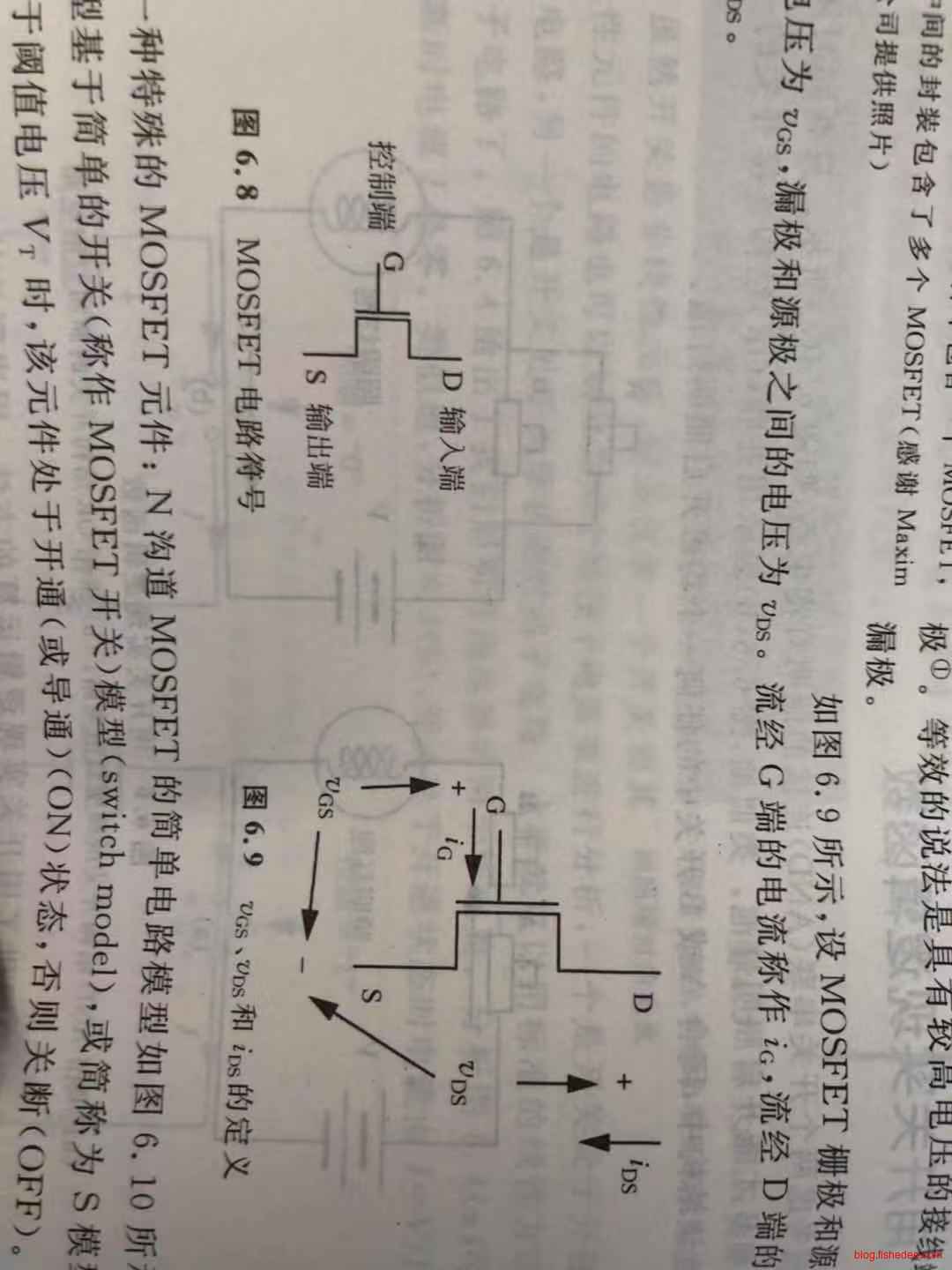
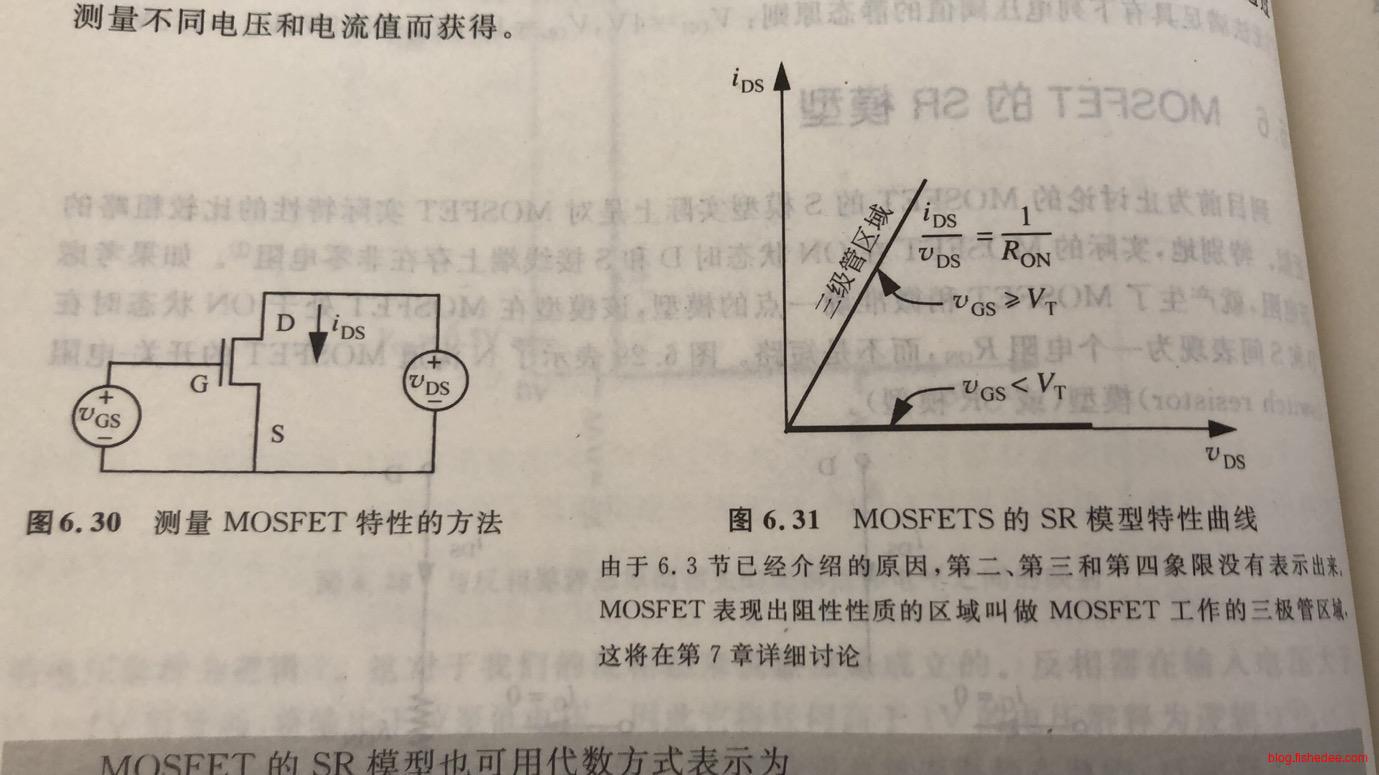
MOSFET控制端称为栅极G,输入端称为漏极D,输出端称为源极S。栅极和源极之间的电压为\(V_{GS}\),漏极和源极之间的电压为\(V_{DS}\),流经G端的电流称为\(i_{G}\),流经D端的电流称为\(i_{DS}\)
7.2 S模型
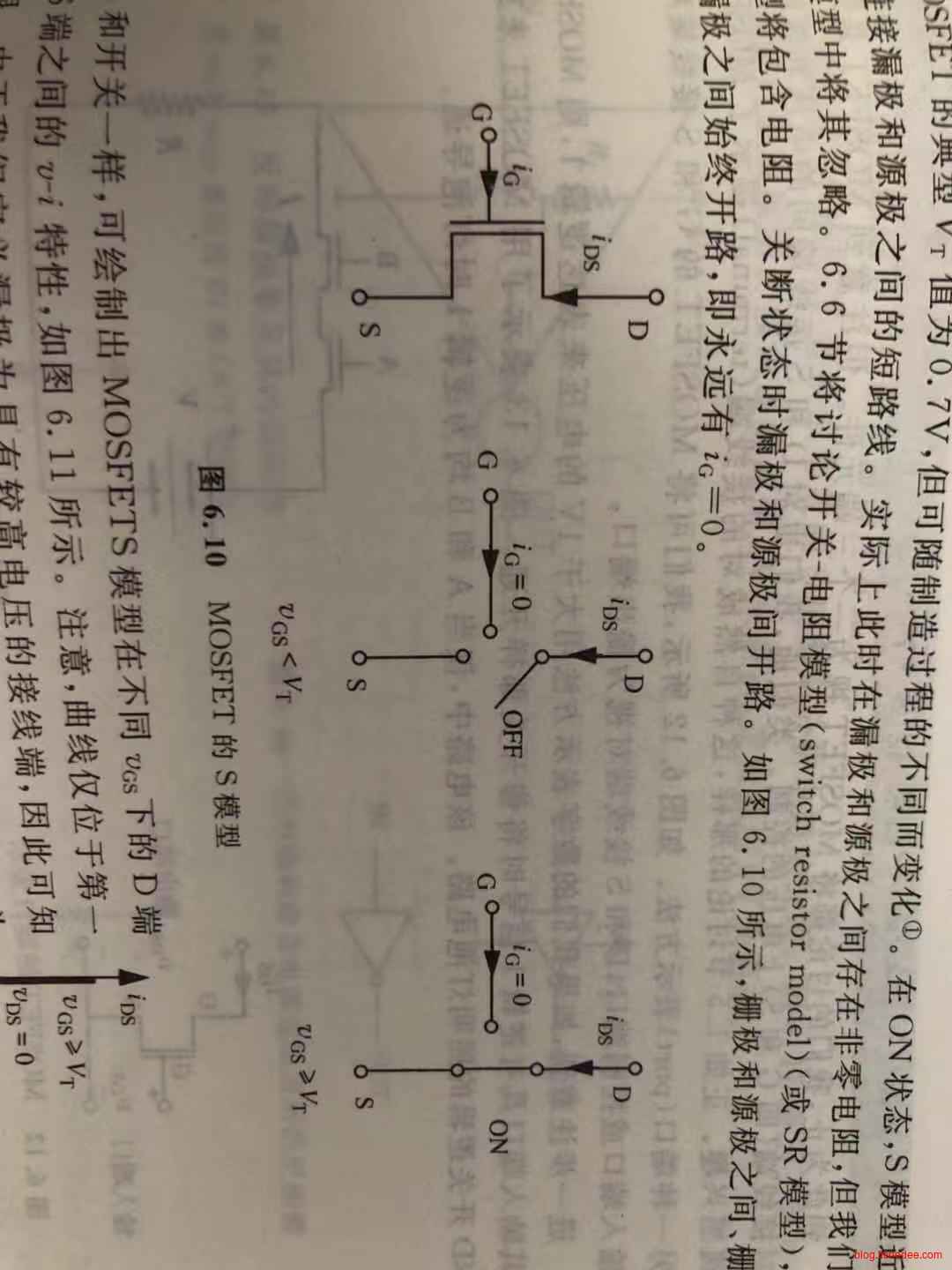
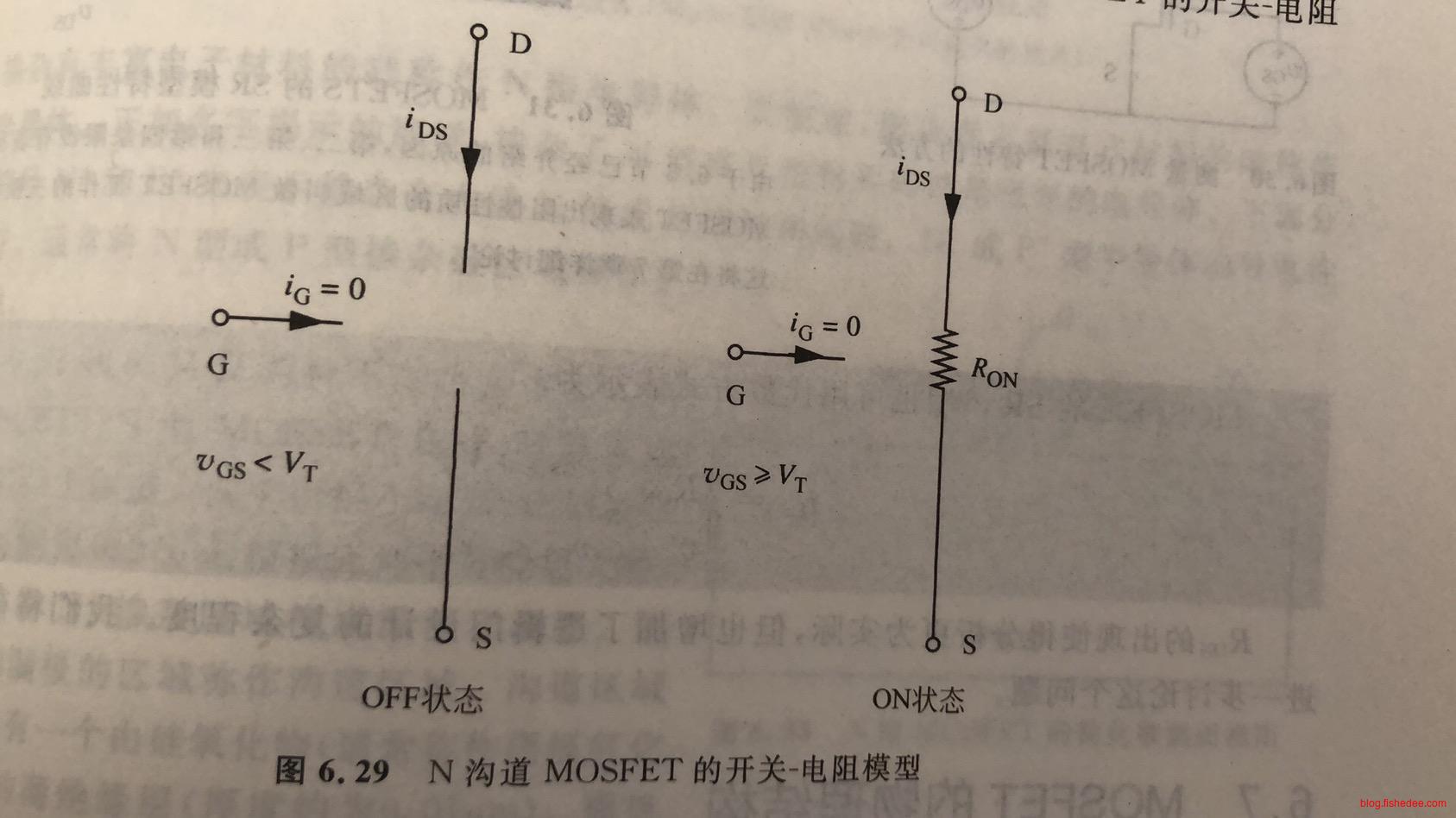
MOSFET的S模型相当简单,当\(V_{GS}\)高于阈值电压\(V_{T}\)(典型值为0.7V)时,该元件处于开通状态(ON),否则关断(OFF)。要注意的是,无论是在开通或者关断的状态,栅极和源极之间,栅极和漏极之间始终开路,即永远有\(i_G=0\)。
代数形式为:
\[ \begin{cases} i_{DS} = 0,如果v_{GS}<V_{T}\\ v_{GS} = 0,如果v_{GS}>=V_{T} \end{cases} \]
7.3 MOSFET实现的逻辑门
7.3.1 非门
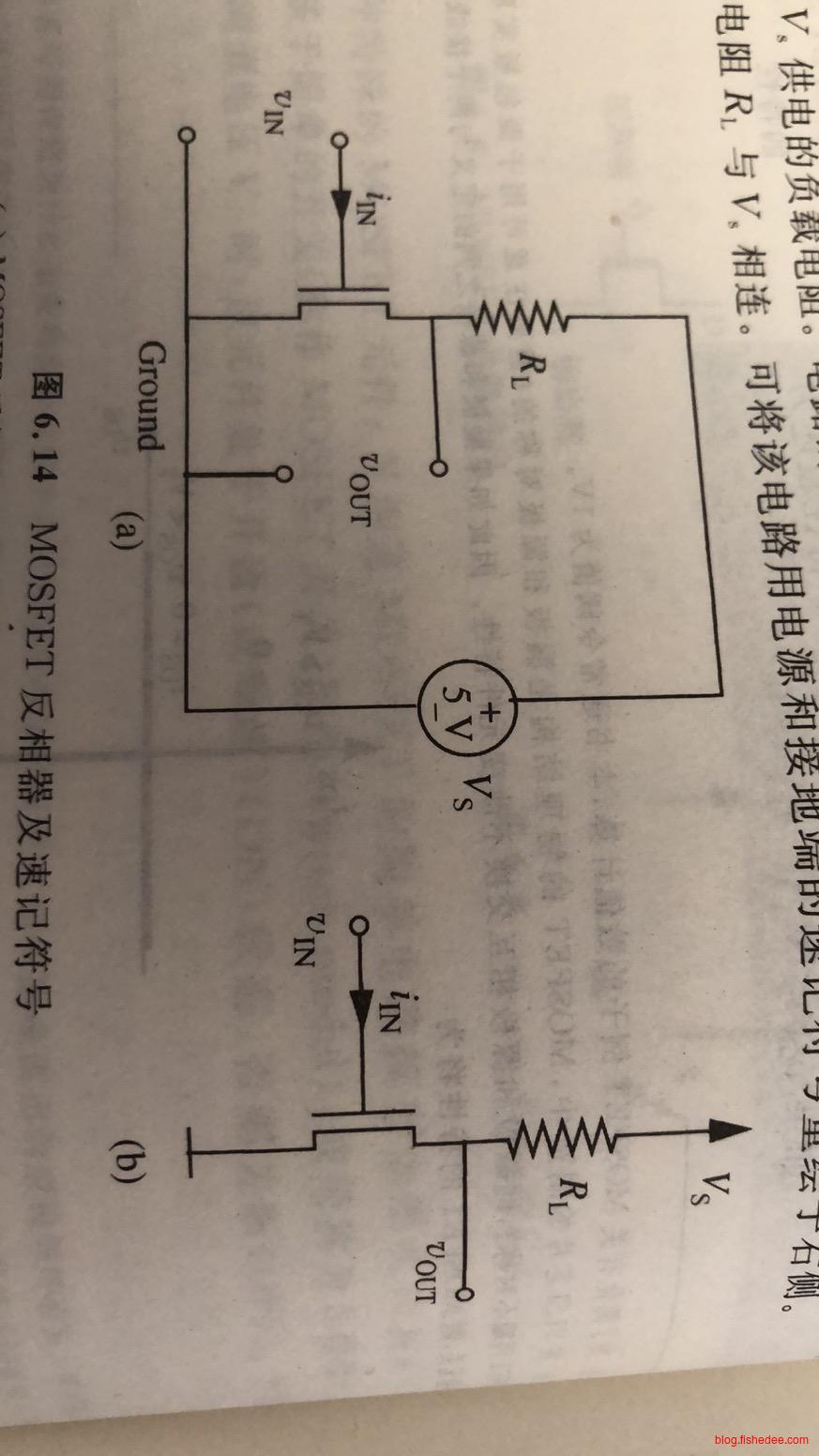
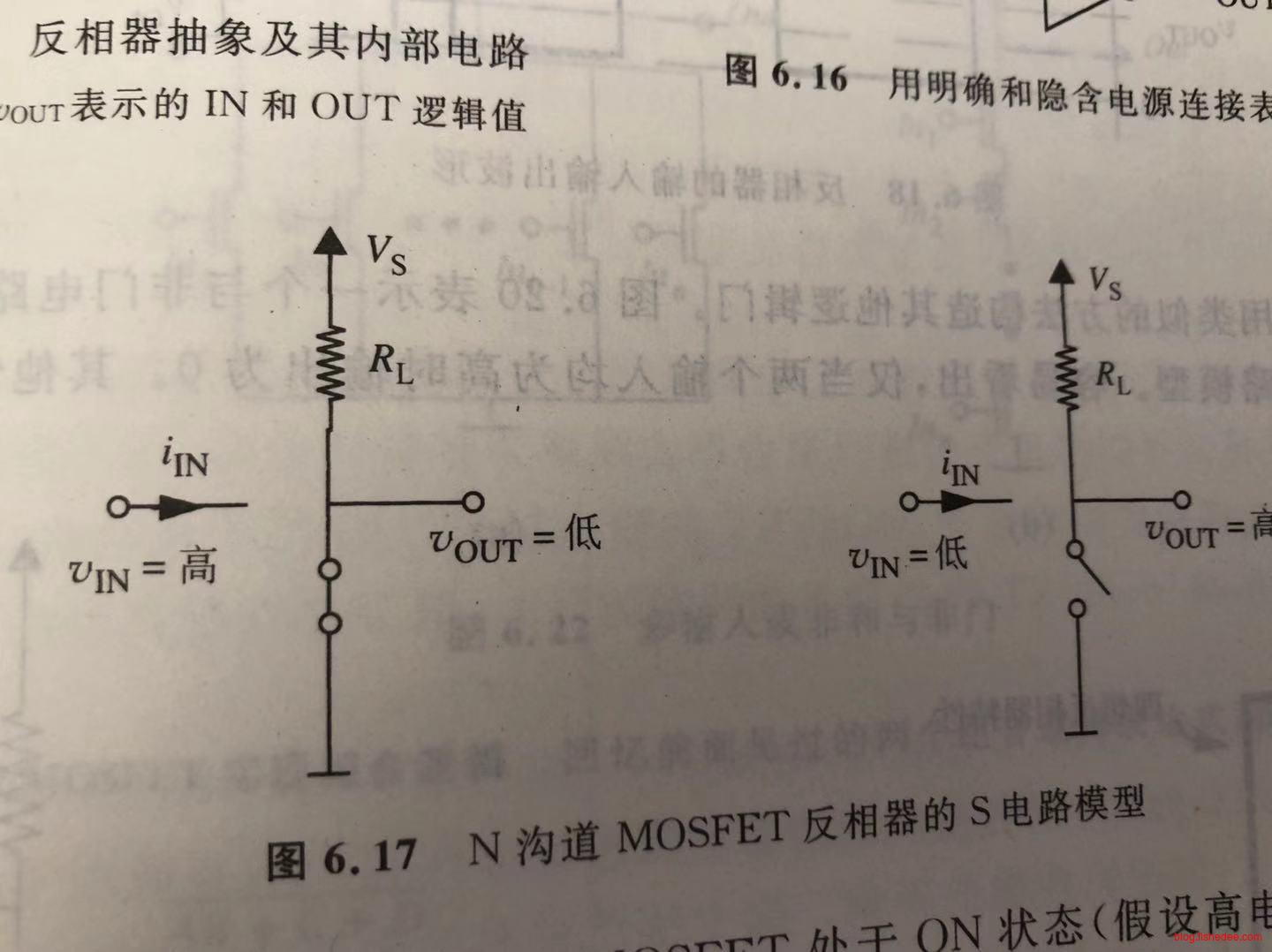
一个MOSFET开关可以实现的非门如上图所示,漏极包含了一个上拉电阻。
我们代入S模型可以得到,当输入为高电平时,MOSFET导通,输出为低电平。当输入为低电平时,MOSFET截止,输出为高电平。注意,MOSFET截止的时候,由于电路是开路的,所以得出这样的结果。如果这个时候输出的后面接入一个低电阻负载,那么输出的电平并不一定是高电平。
| IN | OUT |
|---|---|
| 0 | 1 |
| 1 | 0 |
从真值表中可以看出,这样的确实现了非门逻辑
7.3.2 与非门和或非门
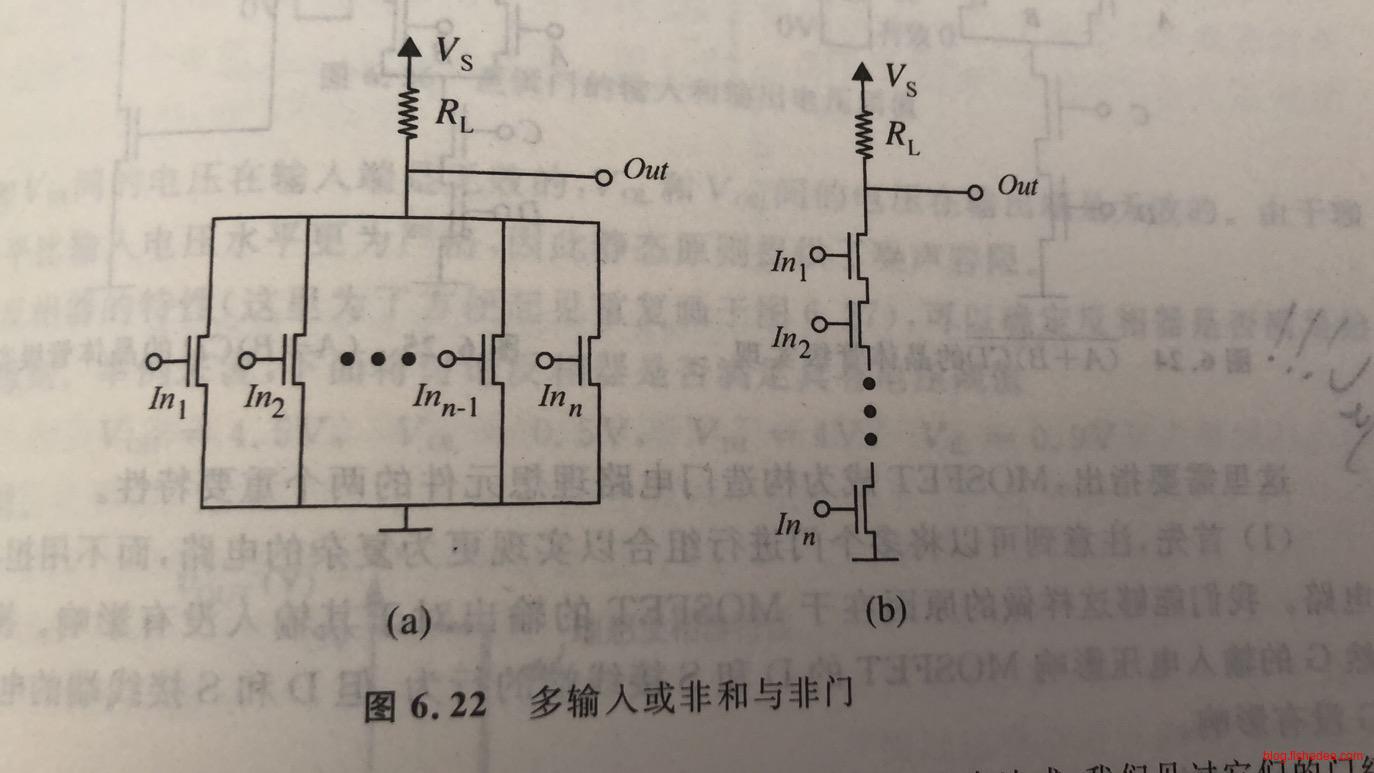
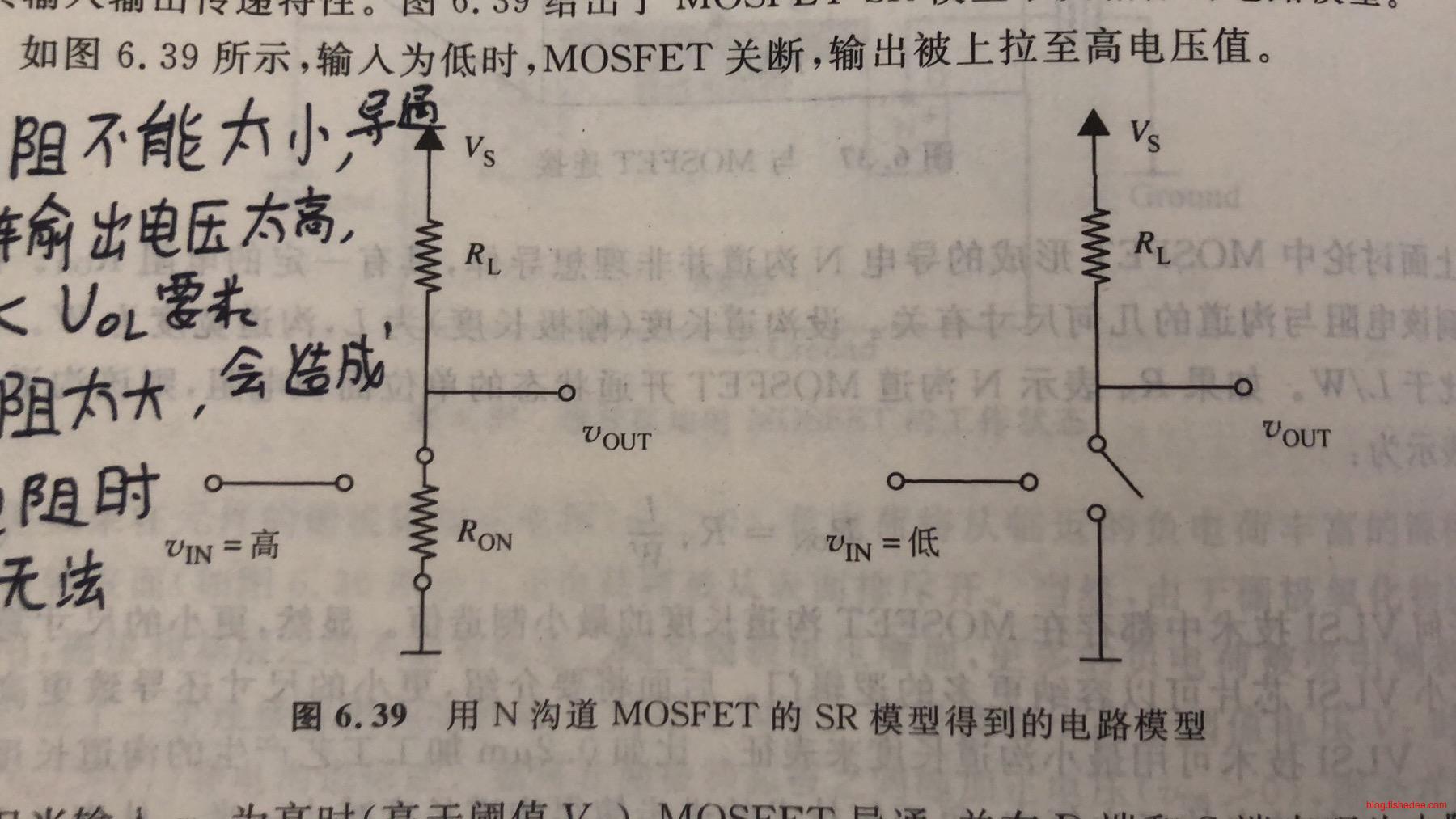
在负载电阻\(R_L\)的下方,通过串联或并联的方法实现了或非门,和,与非门。在左图中,任意一个输入为高电平时,MOSFET开关导通,输出就为低电平,所以为或非门。在右图中,只有所有输入都是高电平时,MOSFET开关才会全部导通,输出才能为低电平,所以为与非门。
7.3.3 多逻辑门组合
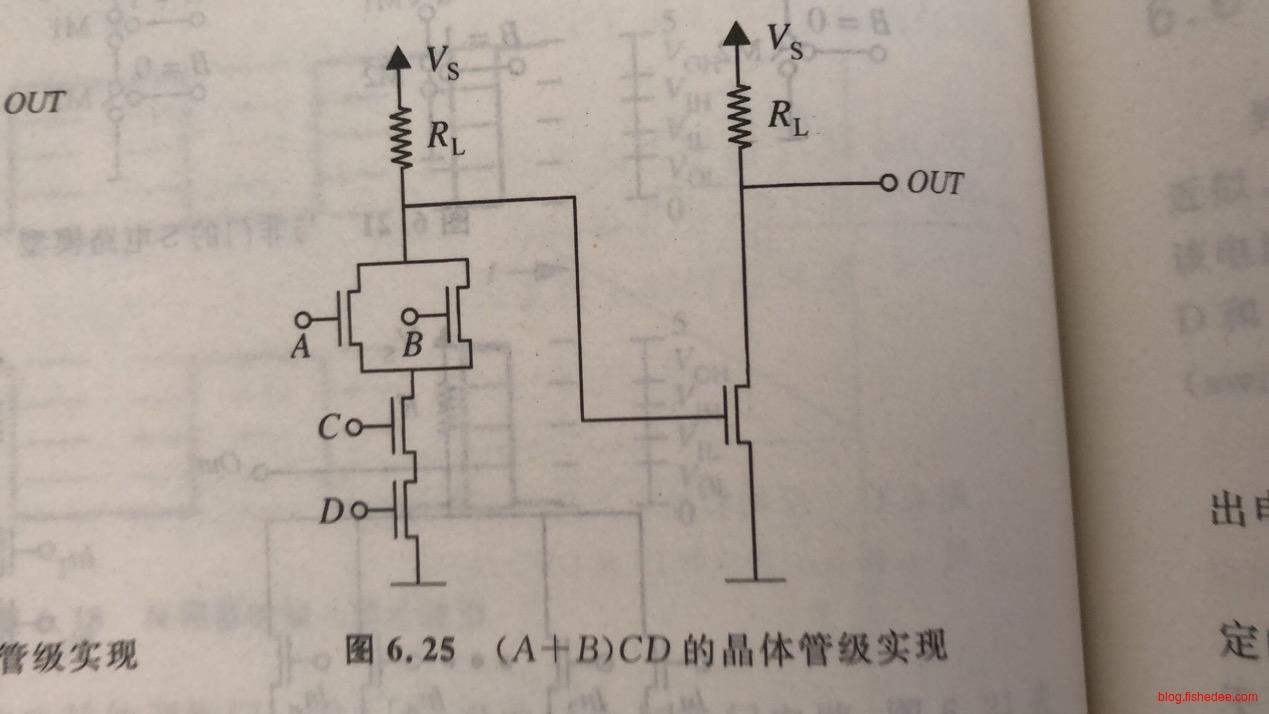
要注意,在7.3.1中,我们指出,非门,输出为高电平,不仅需要输入为低电平,而且对负载也是有要求的,负载也必须为开路。我们尝试将两个逻辑门如上图一样组合出来,当左边的MOSFET输出为高电平时,右边的MOSFET的输入端在栅极,由于栅极总是没有电流通过,也就是总是为开路。所以,这样做是没有问题的,左边的MOSFET肯定为高电平输出。
所以,MOSFET称为构件门电路理想元件的两个重要特性:
- MOSFET的输出对于其输入没有影响。虽然G端的输入电压影响MOSFET的D和S接线端的行为,但D和S接线端的电压或电流对G没有影响。
- MOSFET的栅极G端总是没有电流,相当于无穷大的电阻,使其对与G相连的另一个门的输出没有影响。
7.4 SR模型
MOSFET的S模型实际上是对MOSFET实际特性的比较粗略的近似。一个更好的近似,是使用SR模型。也就是说,当MOSFET在ON状态时,D和S接线端上存在非零电阻。同样地,栅极总是没有电流。另外,对于SR模型的成立,我们有一个附加的严格条件,就是当\(v_{DS}<=v_{GS}-V_T\)时才会成立,也就是栅极电压要足够大的时候,ON状态才会展示出电阻性质。当漏极电压很大的时候,甚至远大于栅极电压时,ON状态就会展示电流源的性质。
在SR模型中,\(R_{ON}\)既会受到当\(v_{GS}\)的影响(\(v_{GS}\)越大时,对应的\(R_{ON}\)就越小),又会受到开关的物理大小影响(开关越大,对应的\(R_{ON}\)就越小)。\(R_{ON}\)的典型值从分立MOSFET的若干毫欧姆(\(m\Omega\))到VLSI实现的MOSFET的若干千欧(\(k\Omega\))不等。
SR模型的代数方程为:
\[ i_{DS} = \begin{cases} \frac{v_{DS}} {R_{ON}}, v_{GS} >= V_T,\\ 0,v_{GS} < V_T\\ \end{cases} \]
SR模型更好地贴近了现实,但是也增加了逻辑门设计的复杂程度。
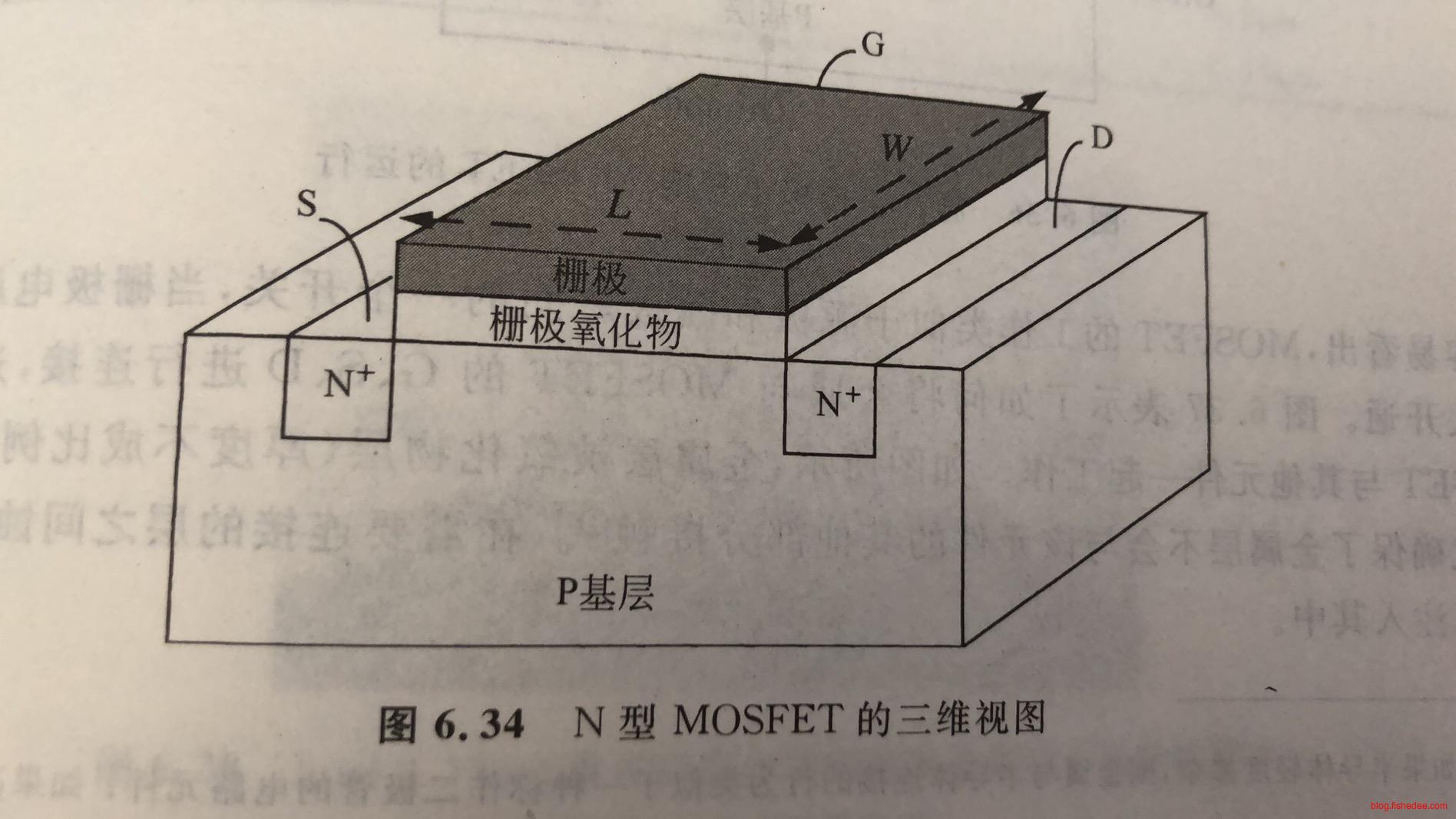
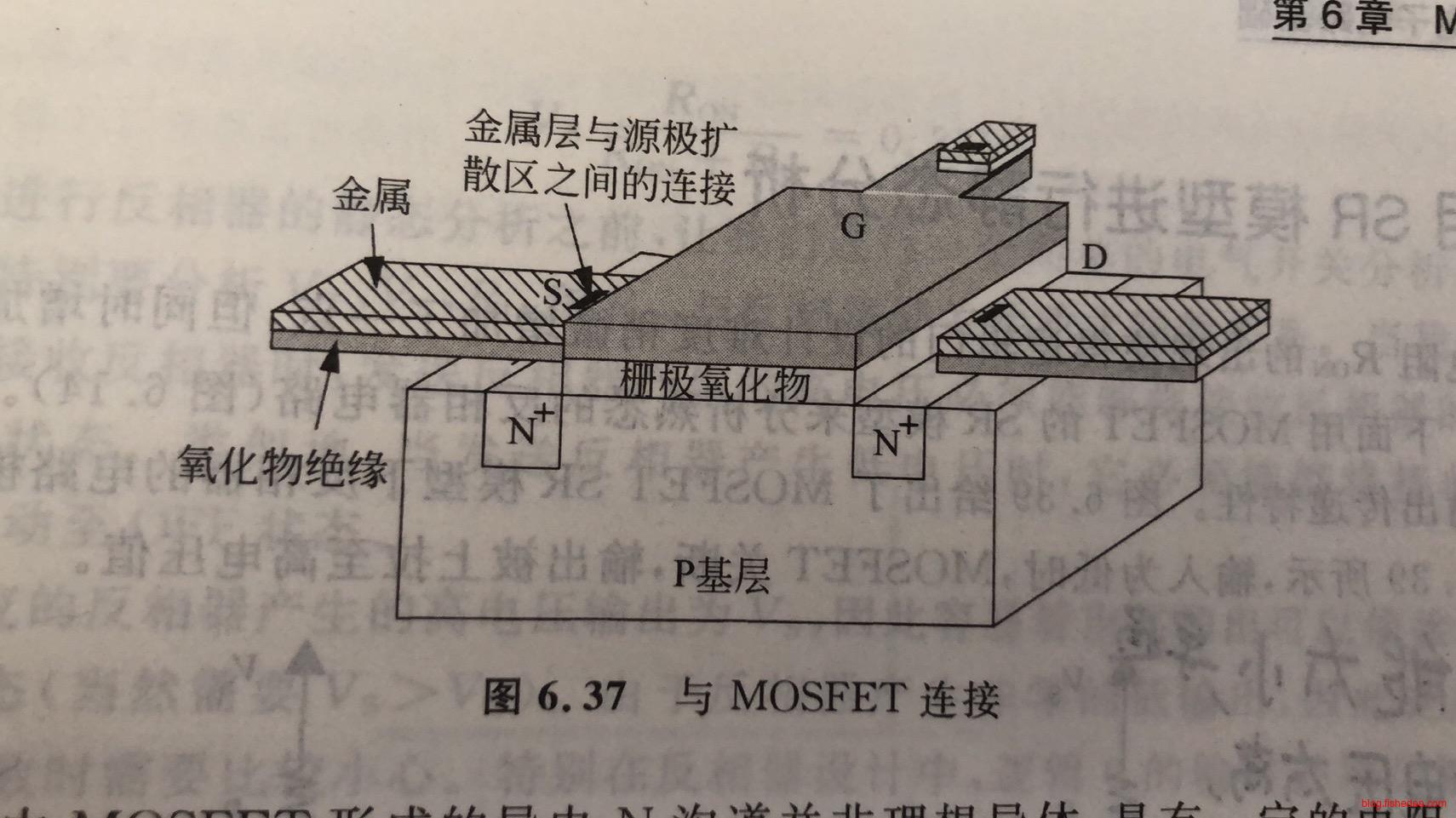
7.5 MOSFET的物理结构
这是MOSFET的三维结构
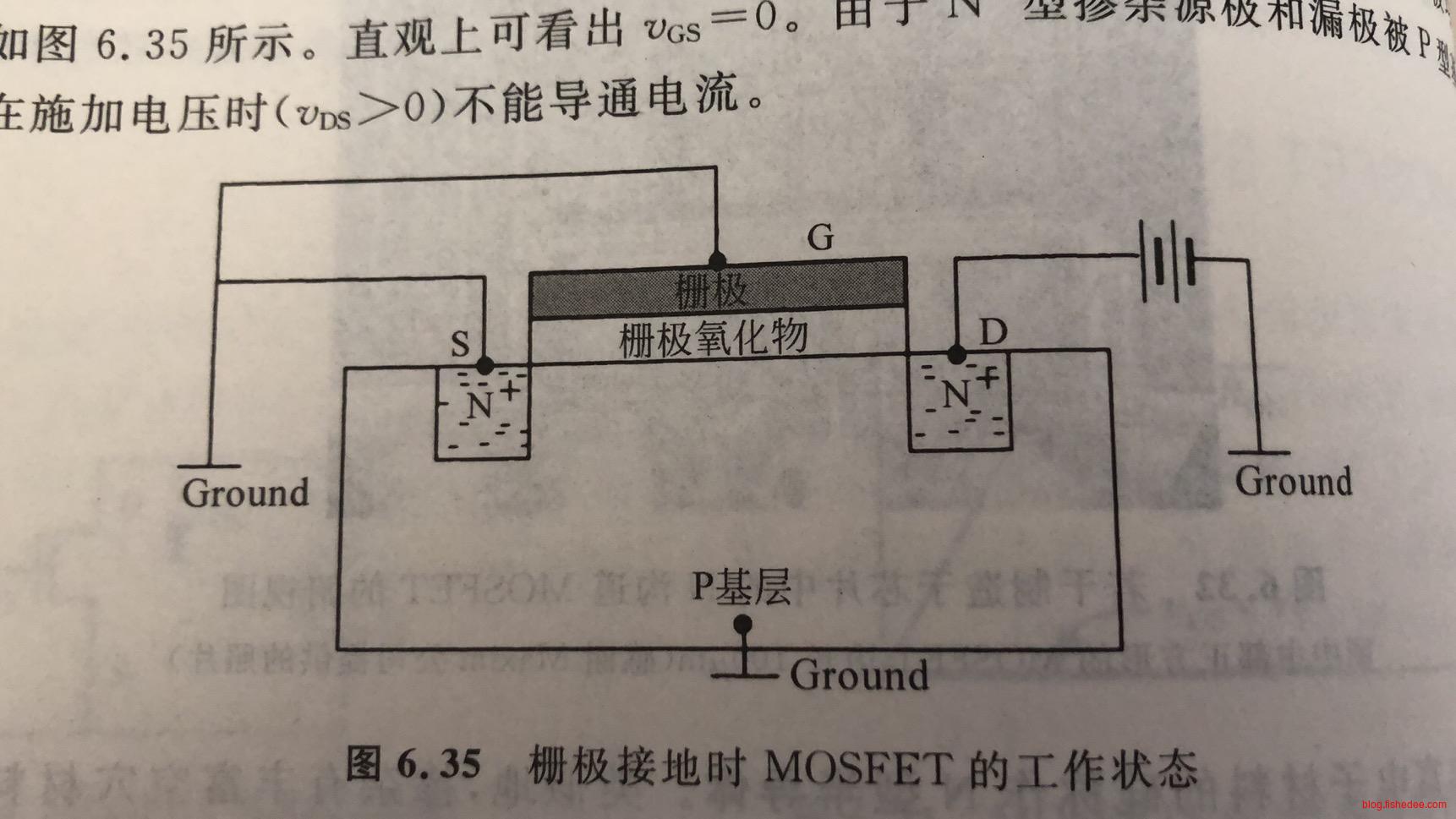
当栅极电压较低时,S和D端之间都是绝缘体,无法导通,MOSFET截止。
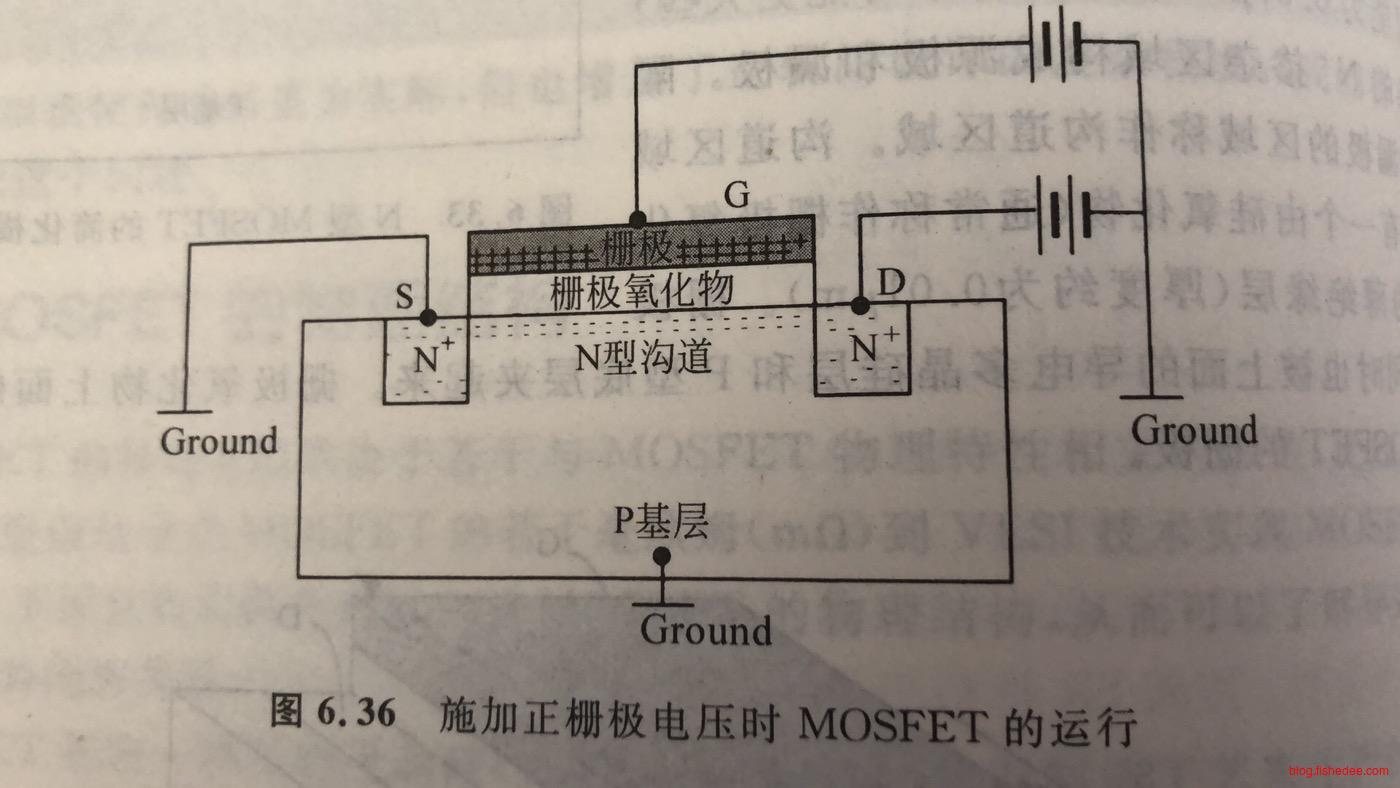
当栅极电压高于\(V_T\)时,负电荷将从负电荷丰富的源极吸引到表面,正负荷从表面被排斥开,直到形成了一个连接源极和漏极的N型导电沟道,这个时候漏极和源极之间就可以导通,允许电流通过。当然,由于栅极氧化物层的绝缘作用,栅极和基层之间不会有电流。
这是MOSFET开关的实际封装图,D和S端上面都有一层绝缘氧化物,它们都需要通过顶部的金属来连接。
7.6 SR模型修正下的逻辑门
有了SR模型后,我们重新考虑非门的设计。由于有了\(R_{ON}\)电阻,当导通的时候,输出电平为:
\[ v_{out} = V_s \frac {R_{ON}} {R_{ON}+R_{L}} \]
为了满足静态原则,以及保证在输出低电平时不会导通下一级的逻辑门,我们需要同时满足:
\[ \begin{cases} V_s \frac {R_{ON}} {R_{ON}+R_{L}} < V_{T} \\ V_s \frac {R_{ON}} {R_{ON}+R_{L}} < V_{OL} \\ \end{cases} \]
所以,这意味着我们在设计MOSFET电路时,\(R_{ON}\)不能太大,或\(R_{L}\)不能太小。
8 MOSFET放大器大信号
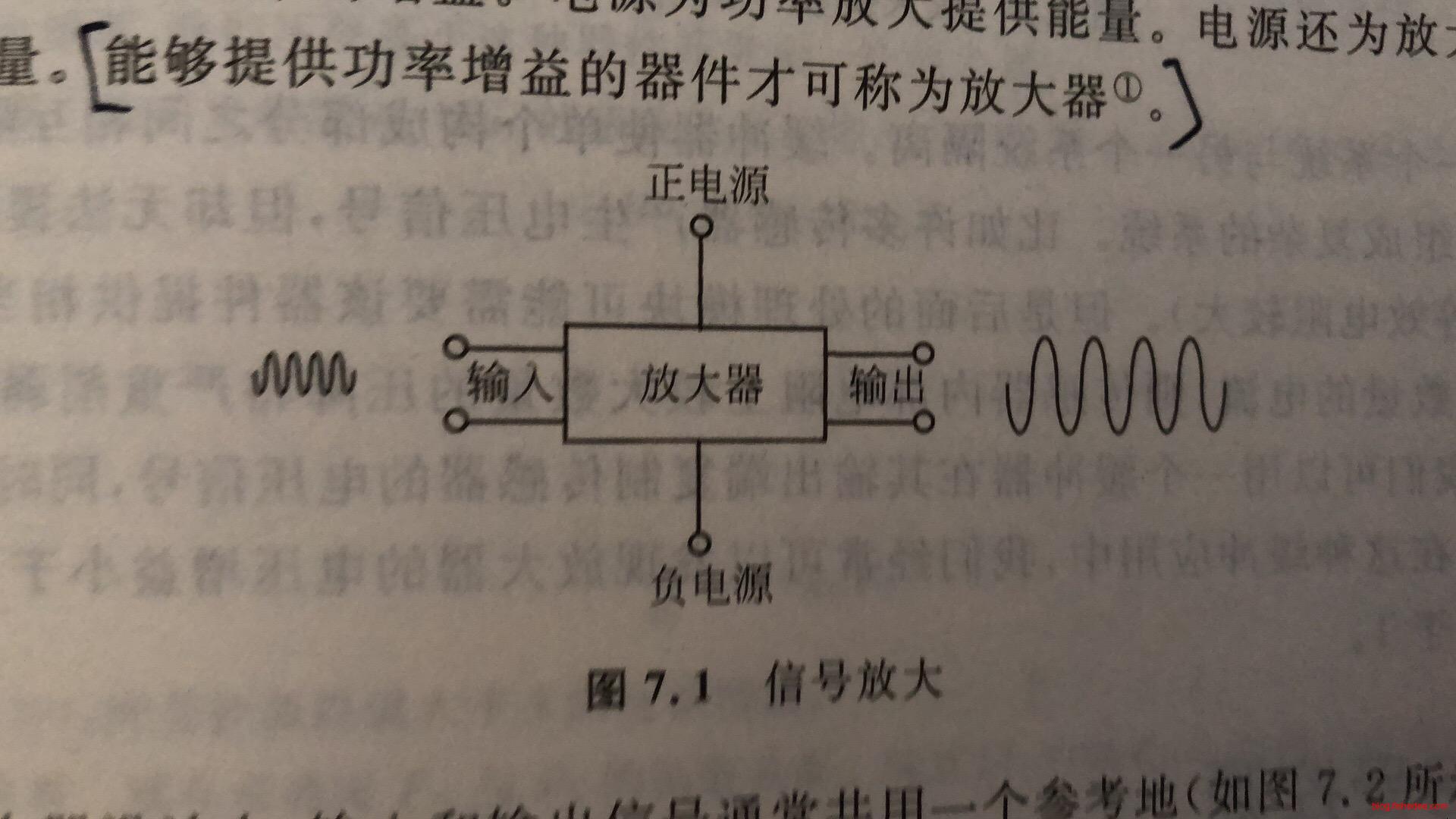
8.1 信号放大
放大器,能够提供功率增益
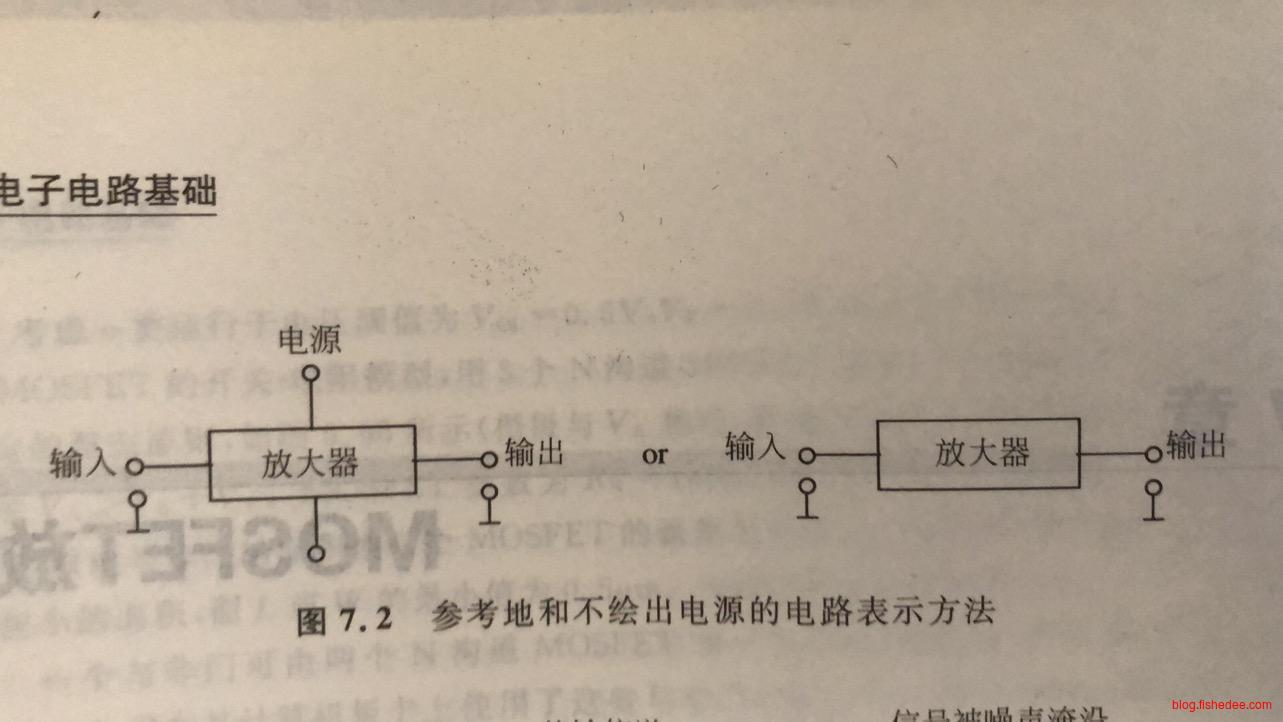
在实际放大器设计中,输入和输出信号通常共用一个参考地。相应地,每个端口都有一个接线端连接到公共的参考地上。
放大器的作用:
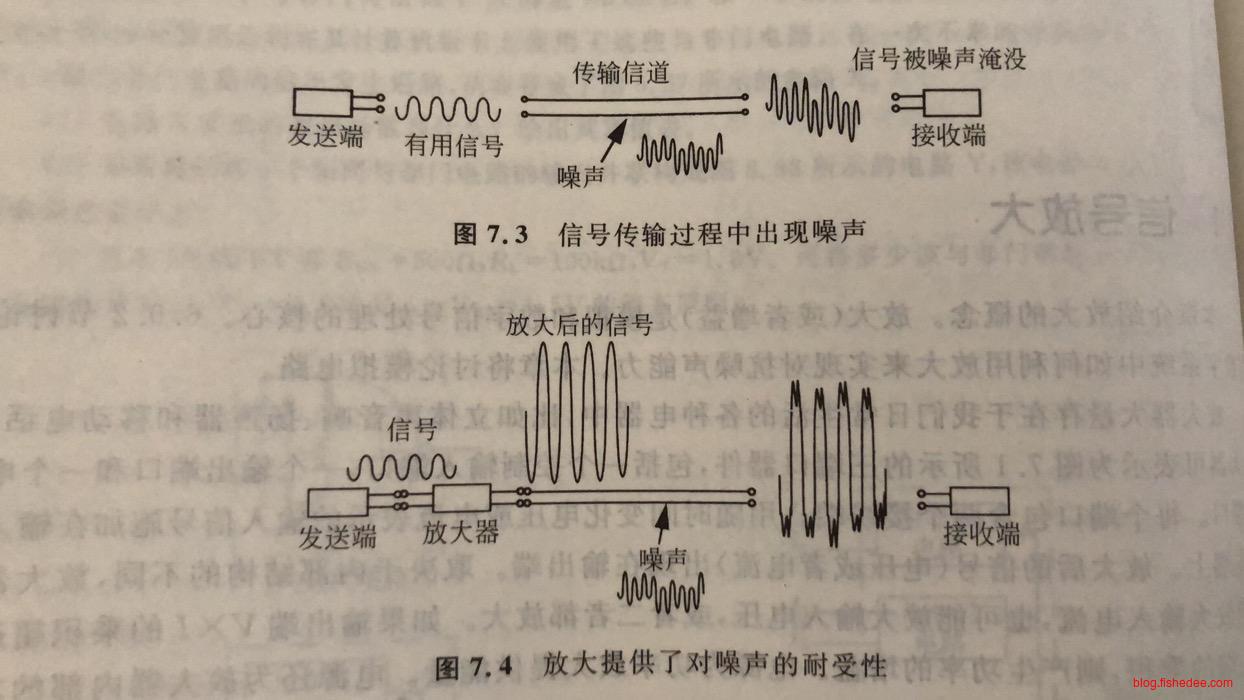
- 提高噪音耐受性
- 缓冲器,在输出端复制输入端的电压信号,同时提供较大数量的电流,将一个系统与另一个系统隔离
8.2 SCS模型
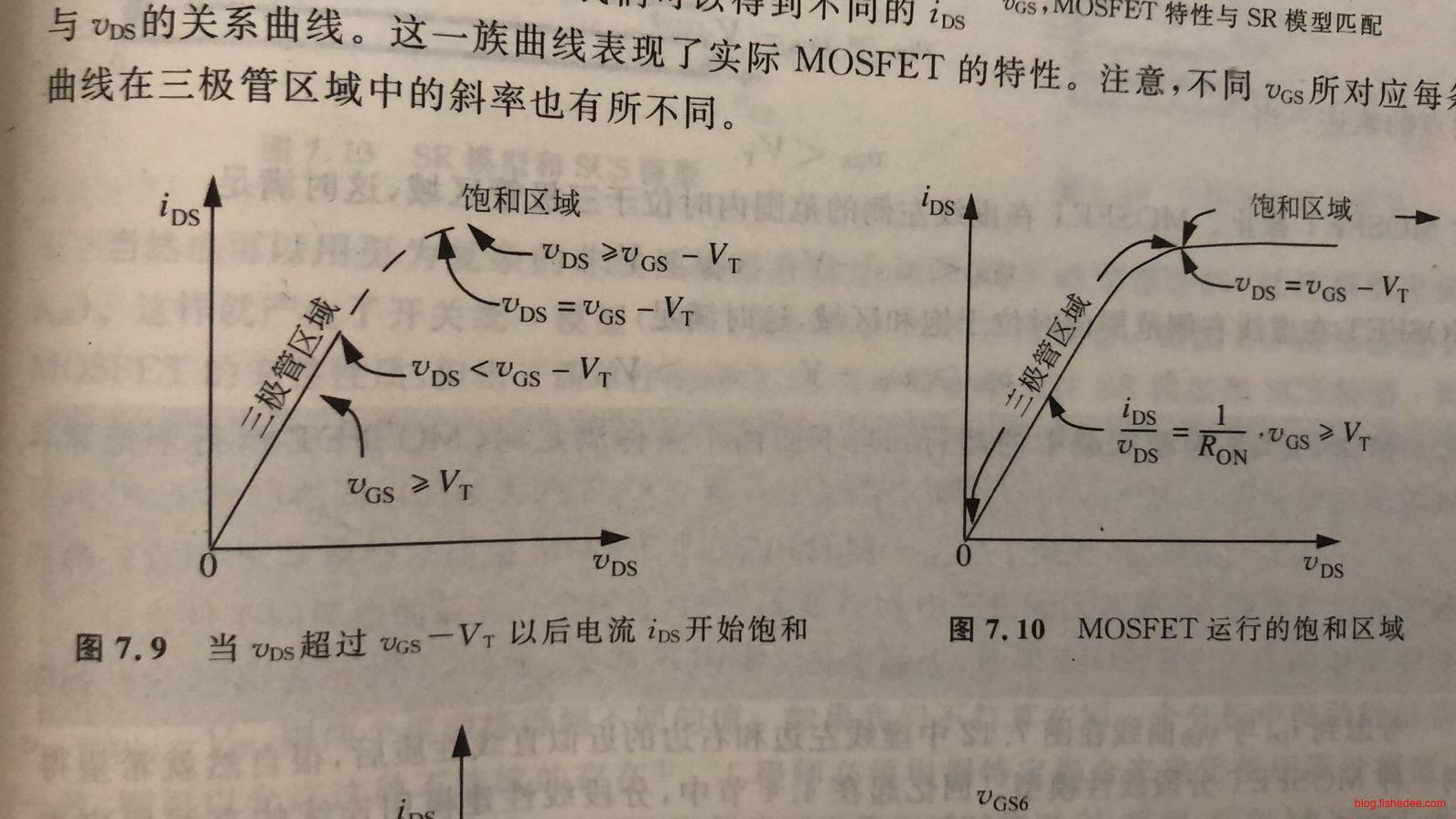
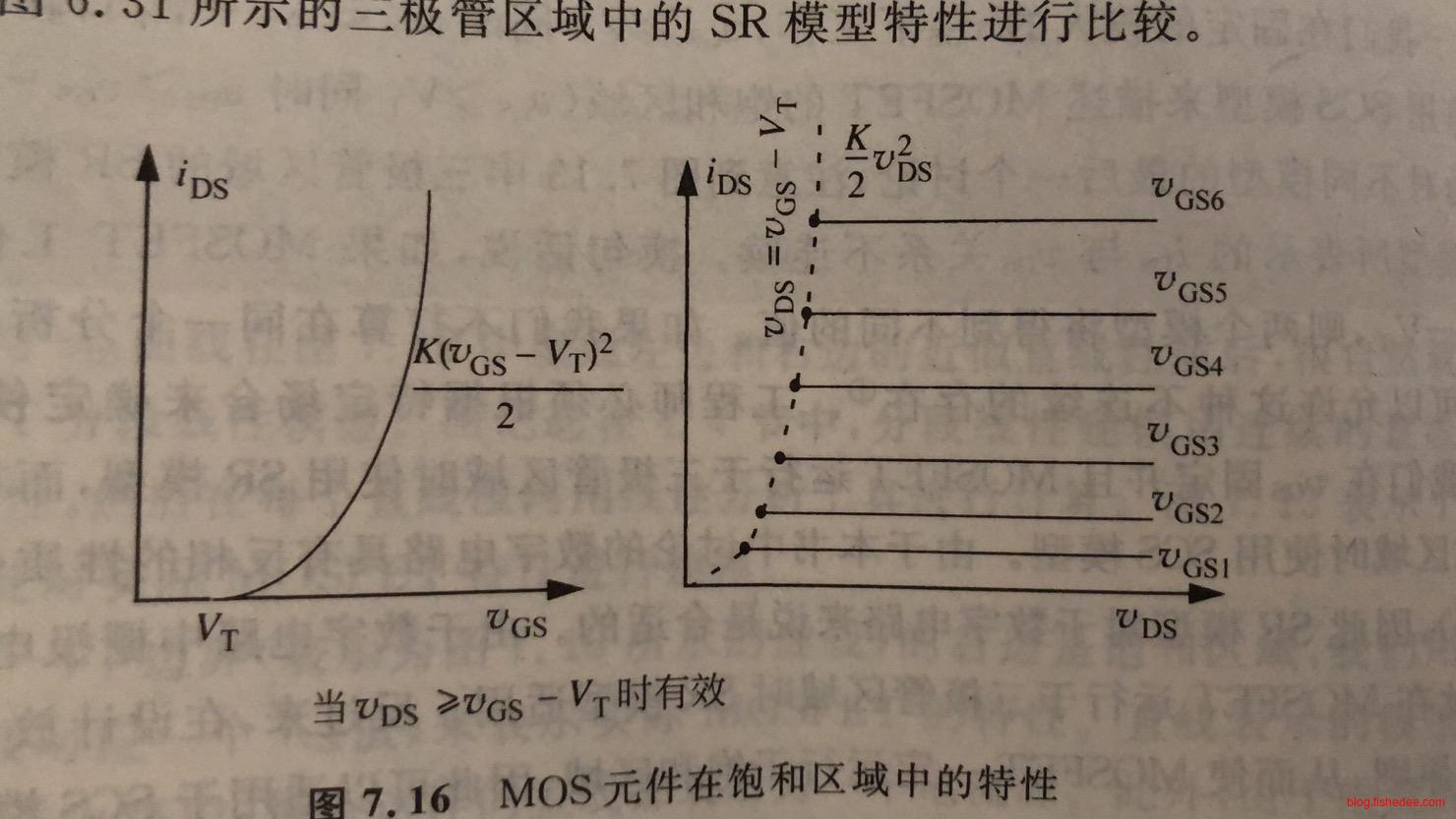
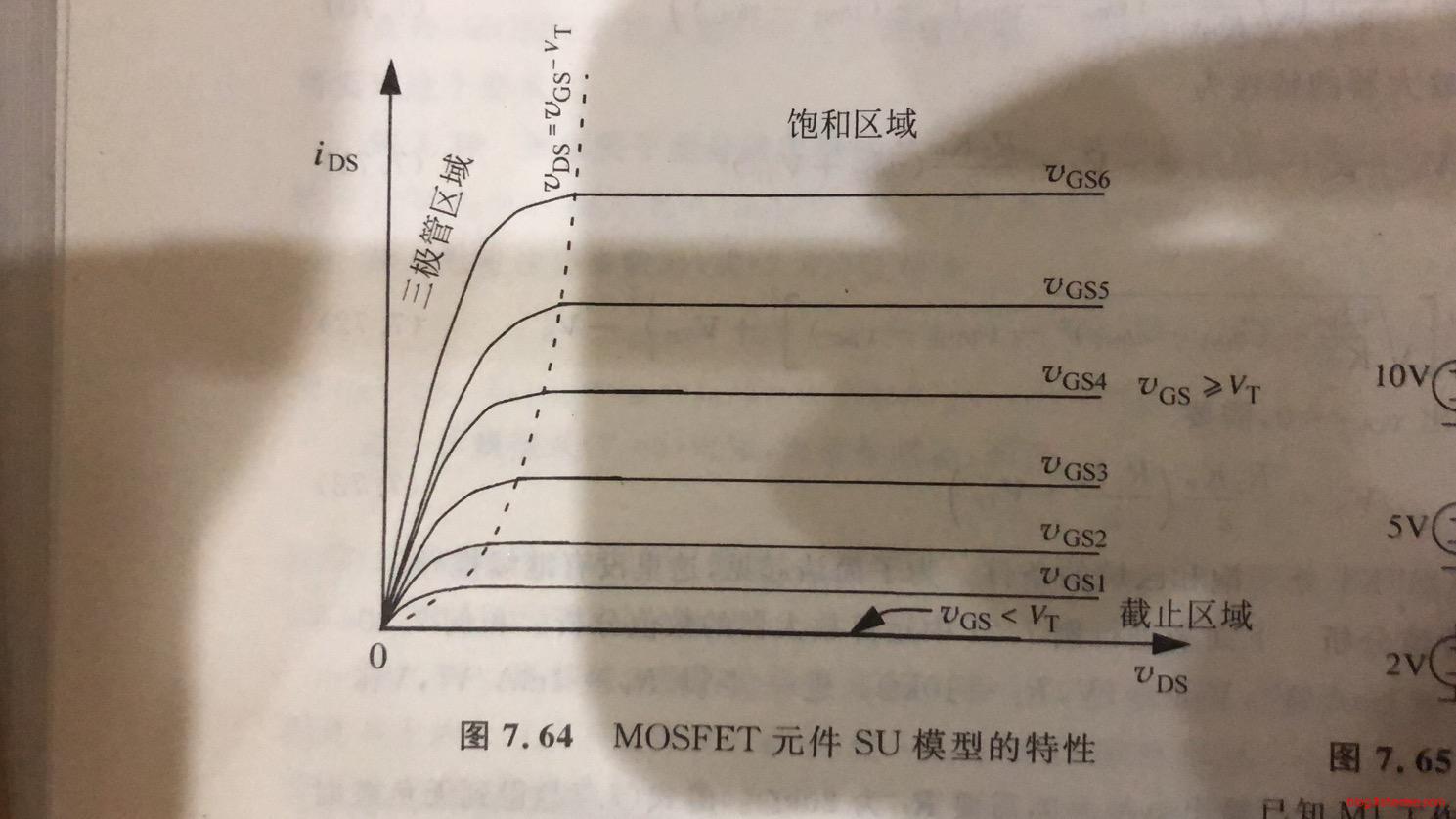
当\(v_{DS}\lt v_{GS}-V_T\)时,SR模型很好地描述了MOSFET的运行性质,这个时候MOSFET运行在三极管区域。但是随着\(v_{DS} \gt v_{GS}-V_T\)时,\(i_{DS}\)曲线变得很平摊,因此将这段区域称为饱和区域。
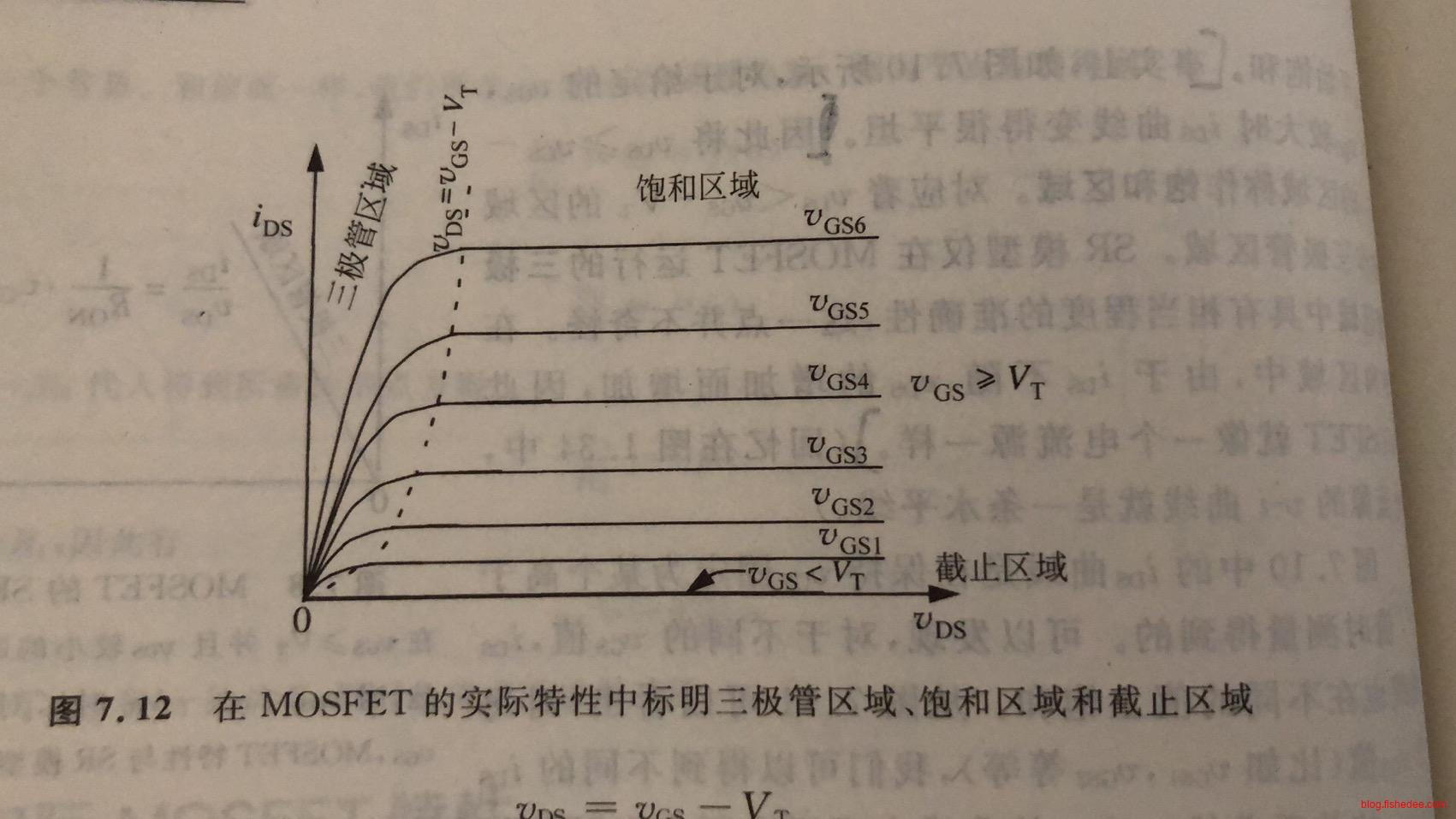
然后,我们画出在不同的\(v_{GS}\)下的MOSFET曲线,得到了完整的MOSFET特性,分别是三极管区域,饱和区域和截止区域。从图中可以看出,\(v_{GS}\)越大,对应的饱和区域下的电流就越大。当然,在特定\(v_{GS}\)下,饱和区域的电流是看作是固定的。
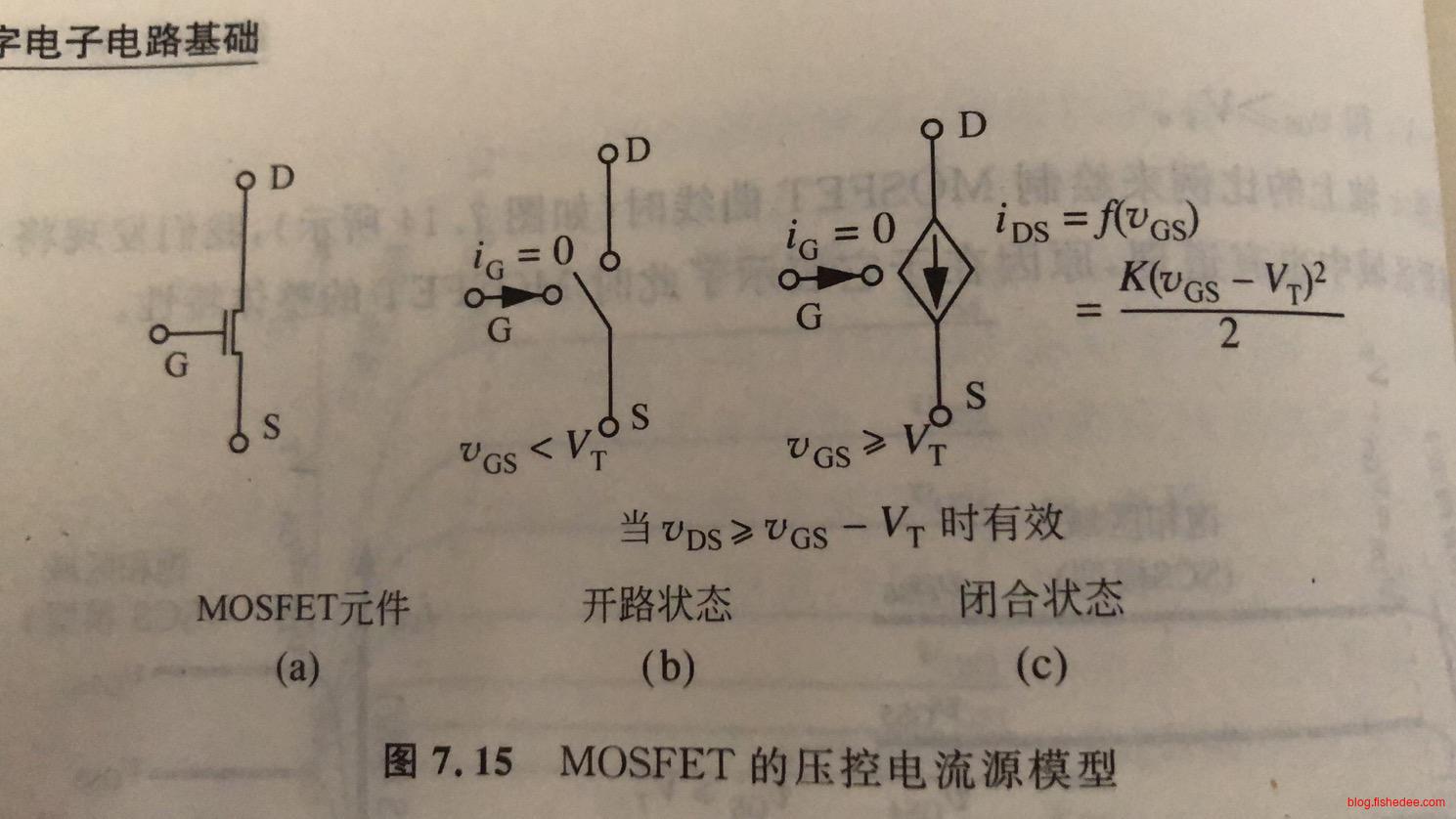
MOSFET的SCS模型就是描述饱和区域下的MOSFET的运行情况,在\(v_{DS}\gt v_{GS}-V_T\)的条件下,当MOSFET截止时,处于开路状态。当MOSFET导通时,MOSFET相当于压控电流源,随着\(v_{GS}\)的增大,所能提供的电流\(i_{DS}\)也在增大。
数学表达式为:
\[ i_{DS} = \begin{cases} \frac {K(v_{GS}-V_T)^2} {2},当v_{GS}>= V_T且v_{DS} >= V_{GS}-V_T时\\ 0,当v_{GS}< V_T时 \end{cases} \]
8.3 MOSFET放大器
8.3.1 电路
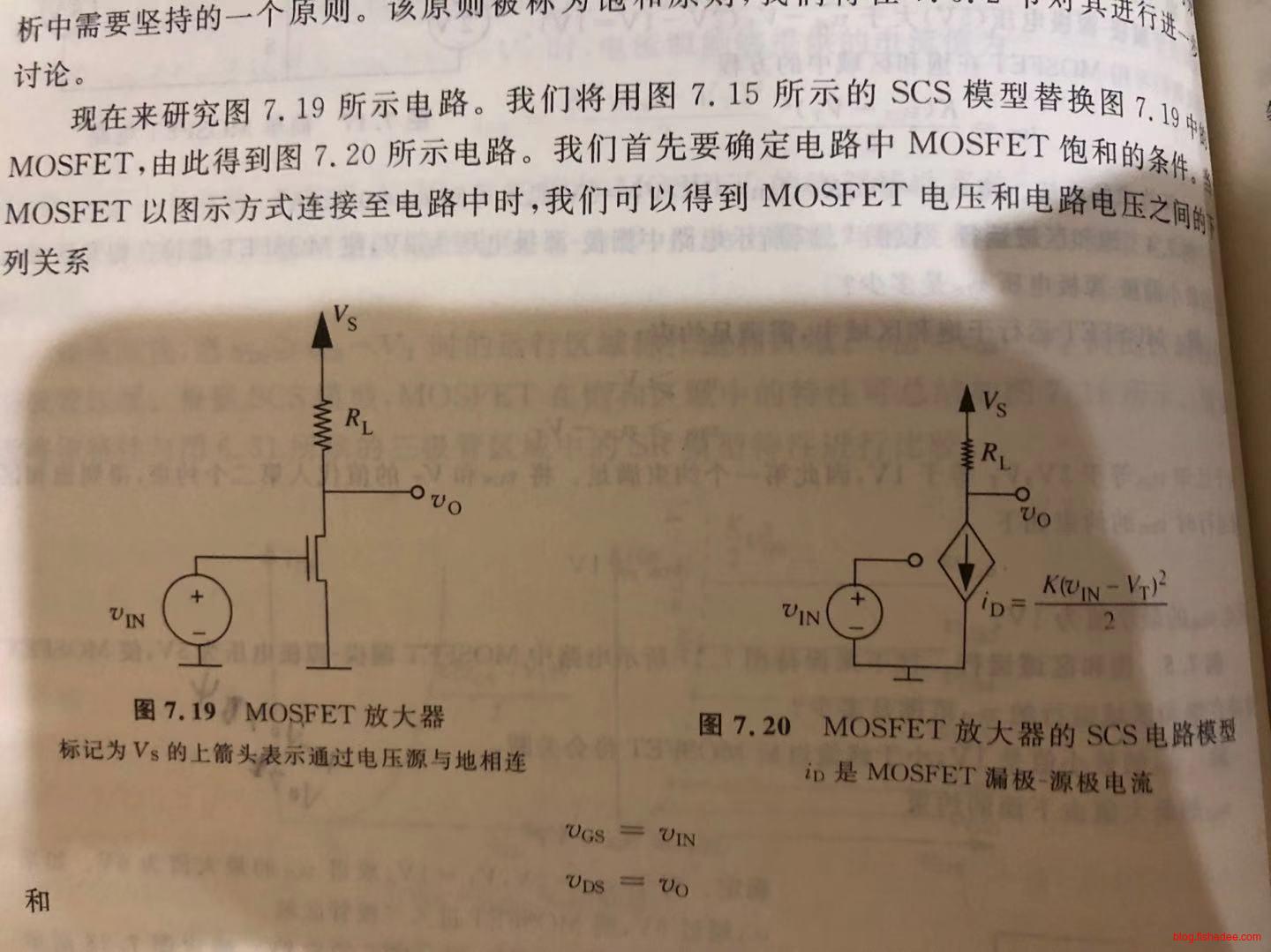
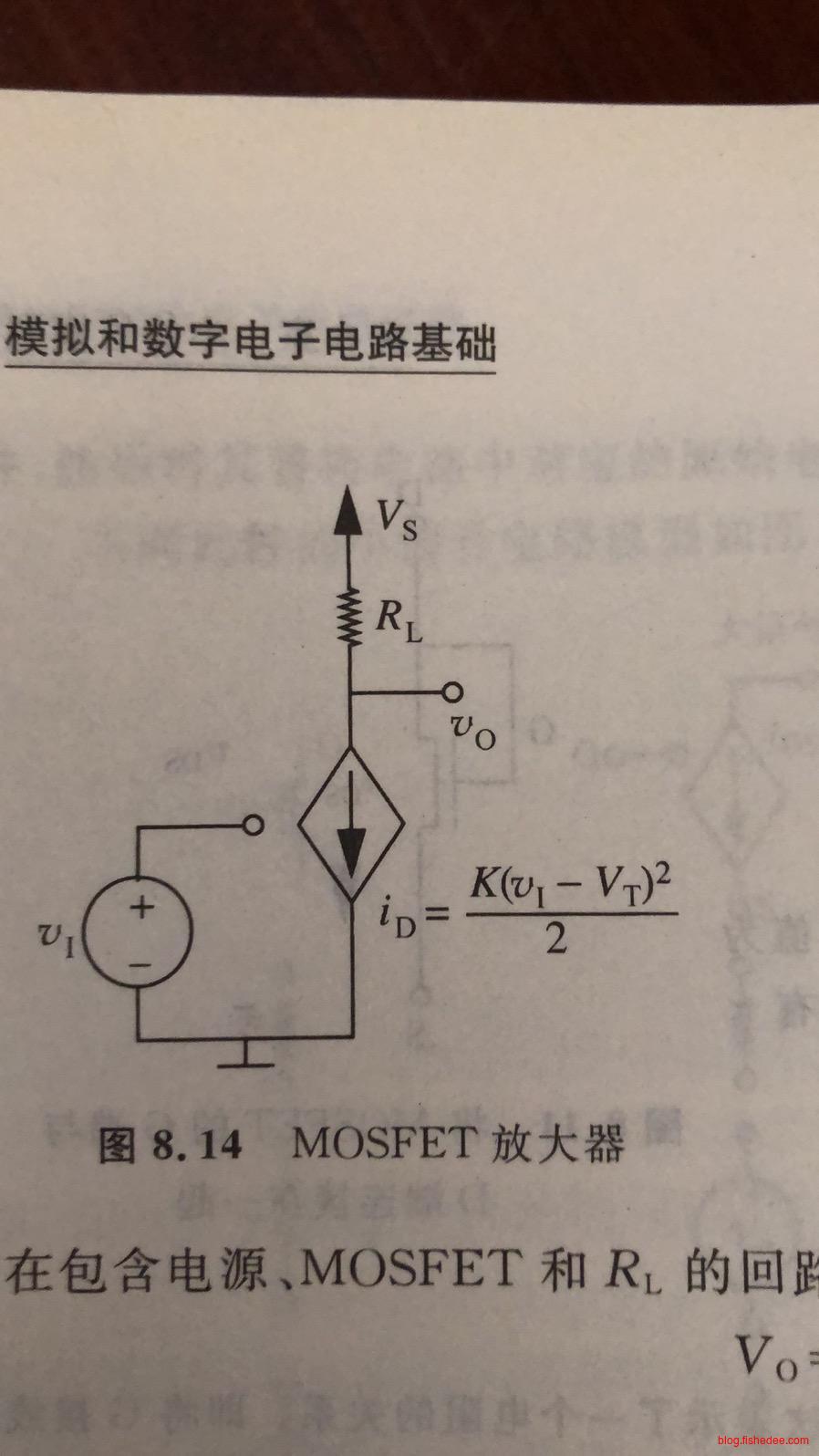
这是MOSFET作为放大器的电路,和非路逻辑门电路一样,但是这个MOSFET是运行在饱和区域的
\[ i_D=\frac {K(V_{IN}-V_T)^2} {2}\\ V_O=V_s - i_DR_L\\ \]
\[ V_O=V_s -\frac {K(V_{IN}-V_T)^2} {2}R_L \]
合并后得到如上图,以及公式,表示了输入电压和输出电压之间的关系。这意味着该放大器是反向的,输入电压越大时,输出电压越小。另外,要让MOSFET工作在放大区域,它需要保证一直在饱和区域中运行,那么输入电压是有限制的范围的。最后,输出电压与输入电压的变化并不是线性的。
8.3.2 输入和输出范围
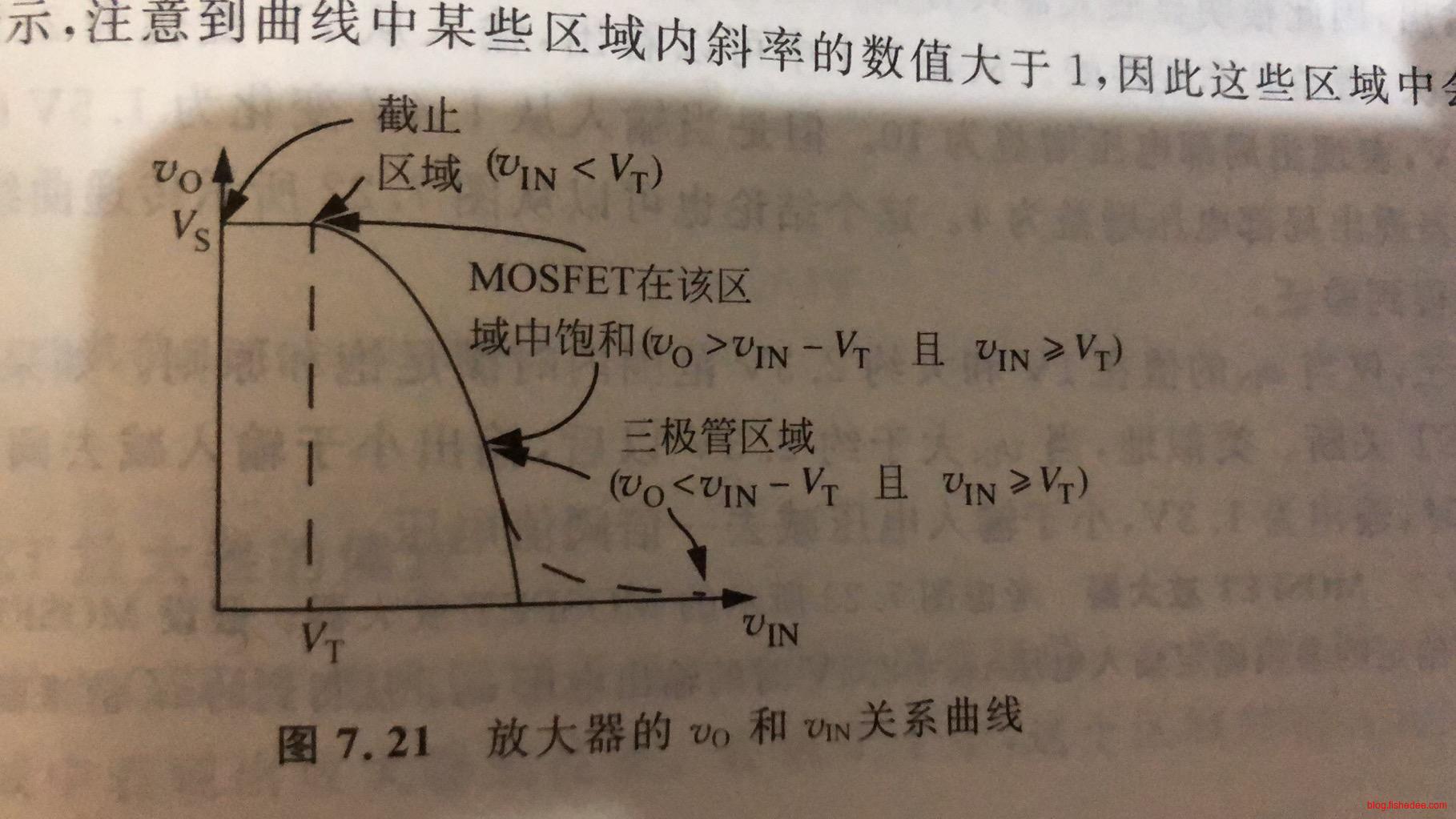
从图中可以看出,只有MOSFET运行在饱和区域,MOSFET放大器才能正常工作,这相当于:
\[ \begin{cases} V_{IN} >= V_T\\ V_O >= V_{IN} - V_T\\ \end{cases}\\ \begin{cases} V_{IN} >= V_T\\ V_{IN} <= V_{O} + V_T\\ \end{cases}\\ \begin{cases} V_{IN} >= V_T\\ V_{IN} <= V_s -\frac {K(V_{IN}-V_T)^2} {2}R_L + V_T\\ \end{cases}\\ \begin{cases} V_{IN} >= V_T\\ V_{IN} <= \frac {-1+\sqrt{1+2V_SR_LK}} {R_LK}+V_T\\ \end{cases} \]
所以,我们得到电压输入范围为:
\[ V_T\to\frac {-1+\sqrt{1+2V_SR_LK}} {R_LK}+V_T \]
对应的电压输出范围为:
\[ V_S\to\frac {-1+\sqrt{1+2V_SR_LK}} {R_LK} \]
8.3.3 偏移工作点
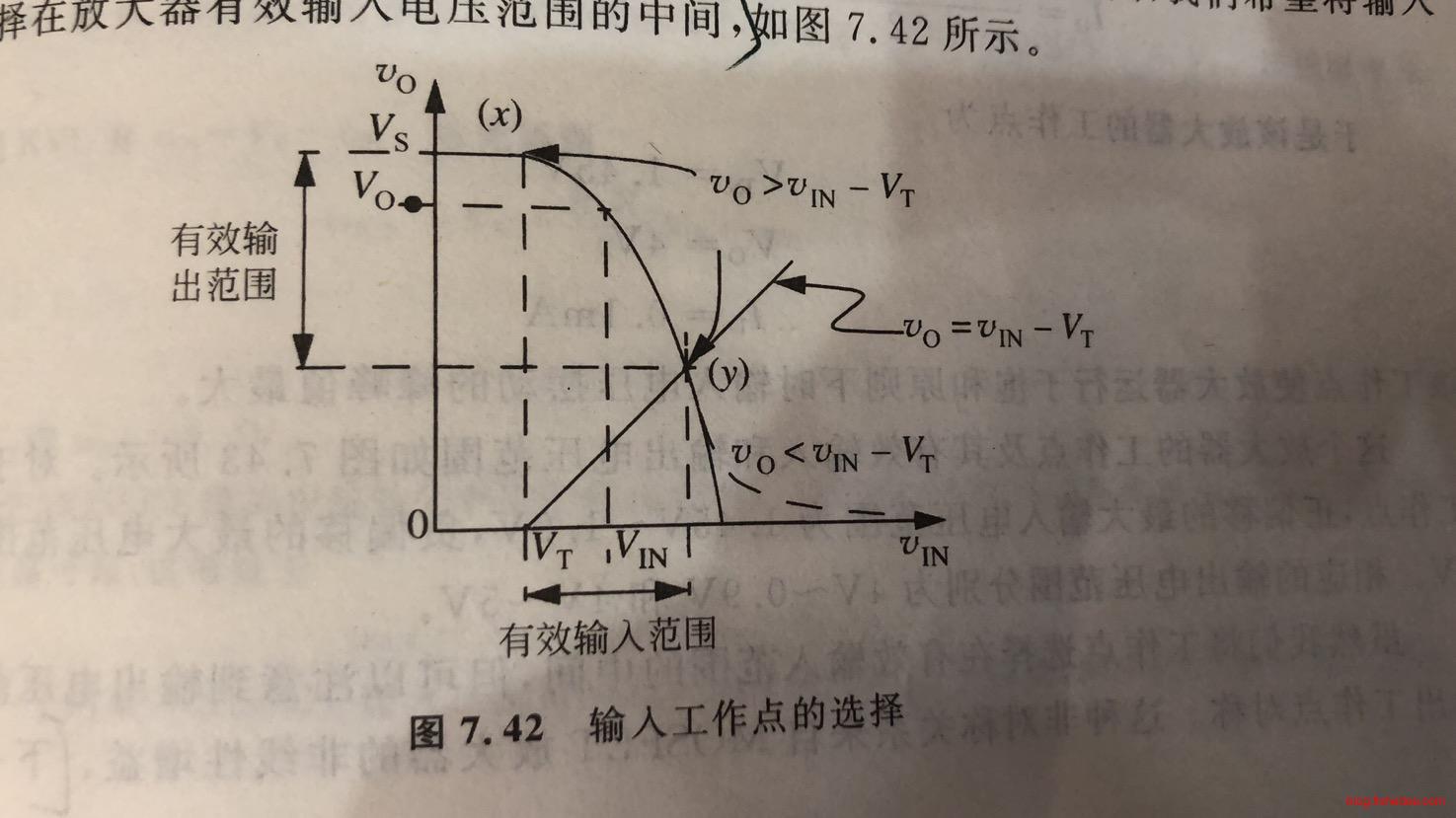
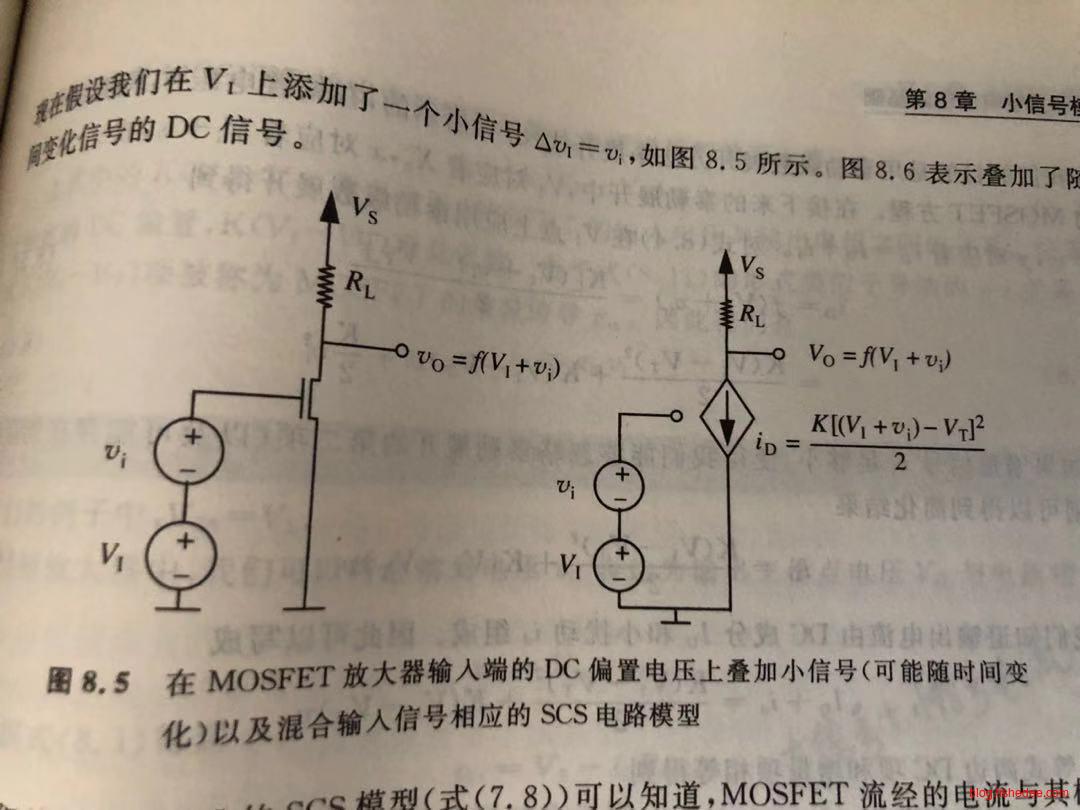
我们通常对放大随时间变化的信号感兴趣,因此需要在随时间变化的输入信号中加入合适的DC偏移电压,从而使得放大器在整个输入电压范围内始终处于饱和区域。
因此,为了获得最大的有用输入范围,我们希望将输入偏置电压选择在放大器有效输入电压范围的中间。
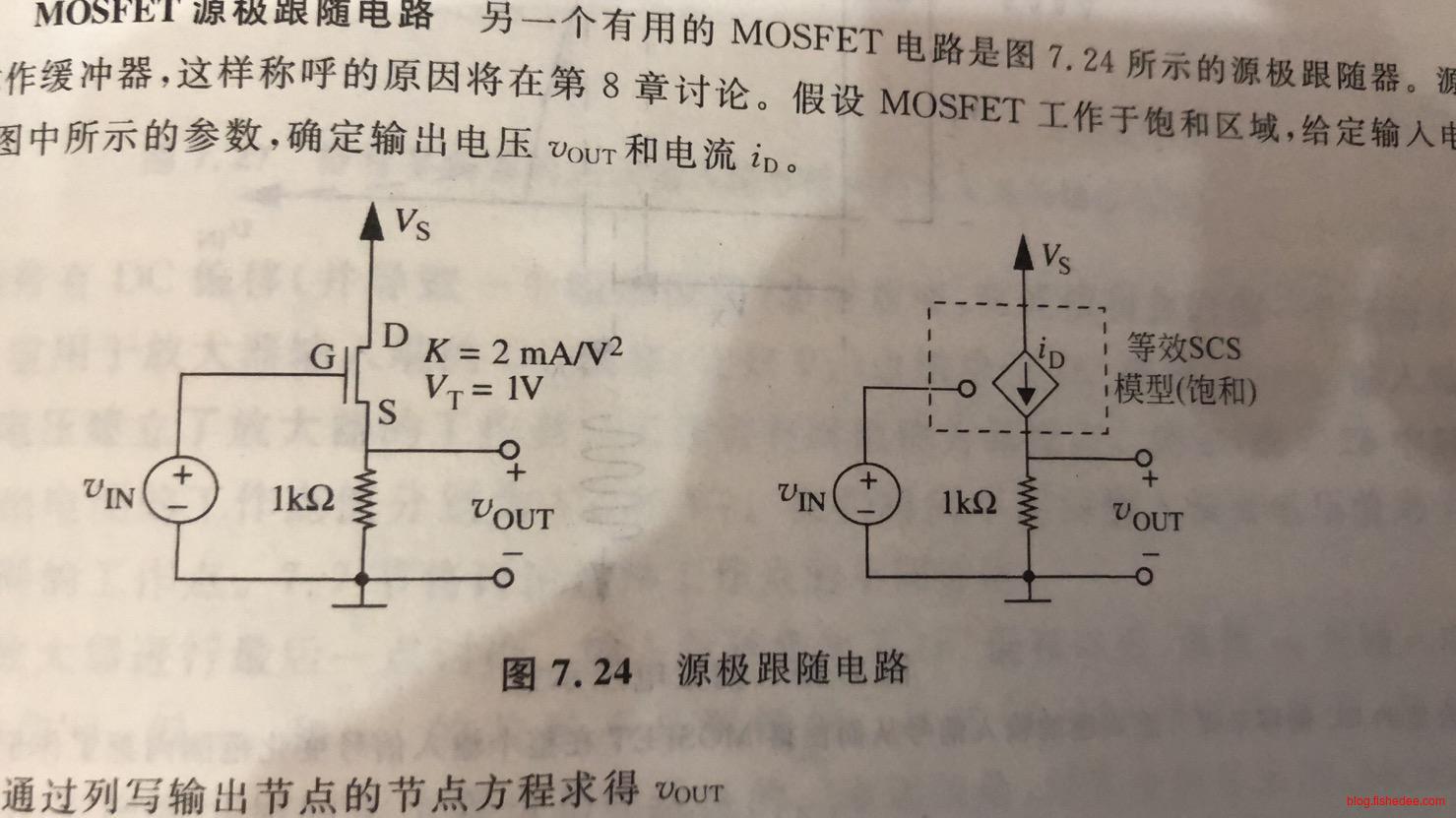
8.4 源极跟随的MOSFET放大器
8.4.1 电路
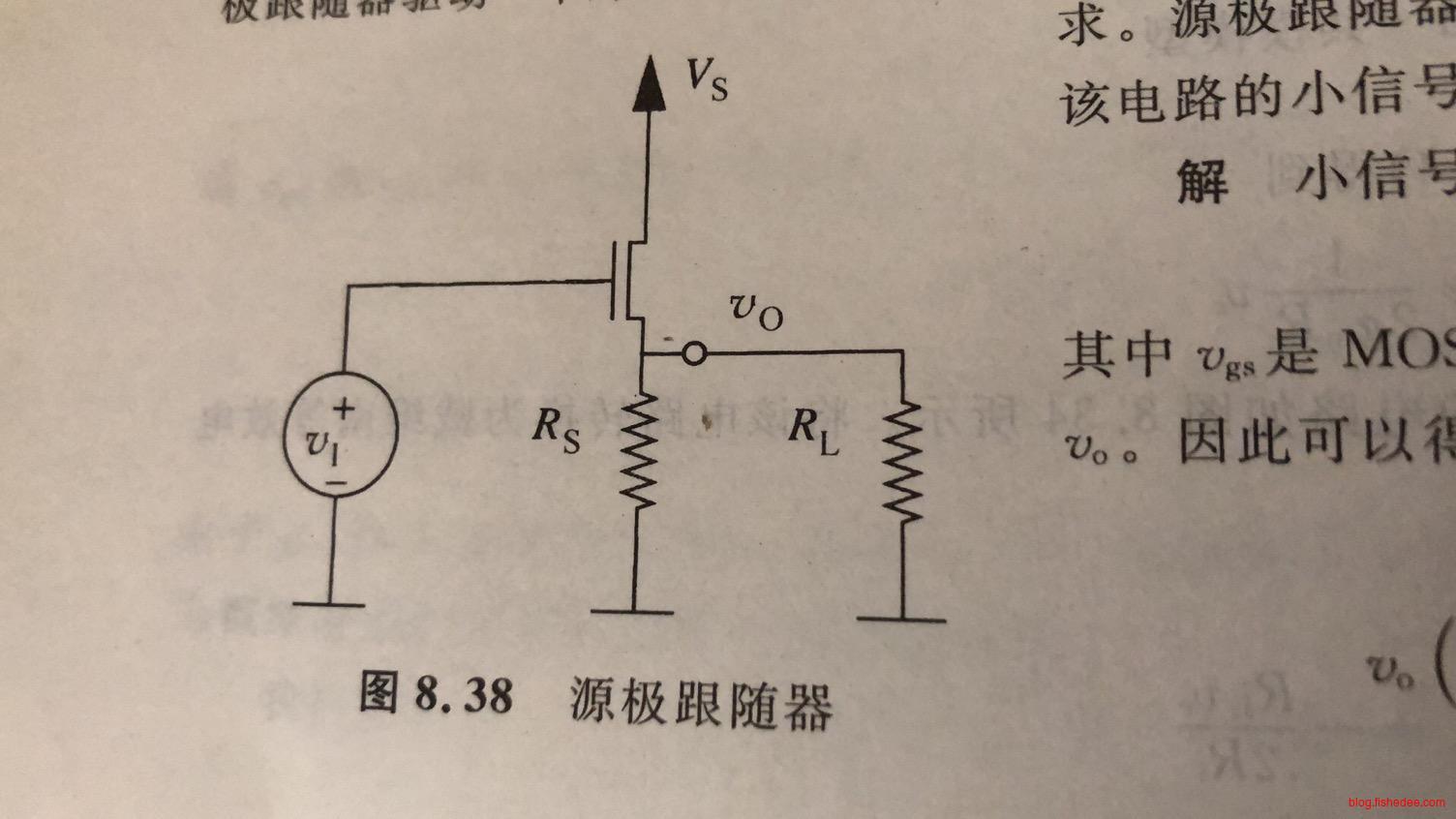
另外一类使用MOSFET作为放大器的电路如上图,称为源极跟随MOSFET放大器,该电路也被称为缓冲器。
\[ i_D = \frac {K(V_{IN}-V_{OUT}-V_T)^2}{2}\\ V_{OUT} = i_DR\\ \]
所以,整理后得到
\[ V_{OUT} = \frac {2(V_{IN}-V_T)+\frac{2}{KR}-\sqrt{[2(V_{IN}-V_{T}+\frac {2} {KR})]^2-4(V_{IN}-V_{T})}}{2} \]
显然,该电路也是非线性的,但是是正向电路。
8.4.2 输入和输出范围
要让该电路正常运行,那么MOSFET需要一直在饱和区域运行,也就是
\[ \begin{cases} V_{IN}-V_{OUT}-V_T<=V_s-V_{OUT}\\ V_{IN}-V_{OUT} >= V_T \end{cases}\\ \begin{cases} V_{IN}<=V_s+V_T\\ V_{IN}-V_{OUT} >= V_T\\ \end{cases} \]
另外,由于\(V_{OUT}\)最小值为0,所以,上方程化简为:
\[ \begin{cases} V_{IN}<=V_s+V_T\\ V_{IN}>=V_T\\ \end{cases} \]
所以,输入电压范围为:
\[ V_T\to V_s+V_T \]
输出电压范围为:
\[ 0 \to \frac {2(V_s)+\frac{2}{KR}-\sqrt{[2(V_s+\frac {2} {KR})]^2-4(V_s)}}{2} \]
8.4.3 偏移工作点
偏移工作点就是输入电压电压范围的中点,这点就不啰嗦了
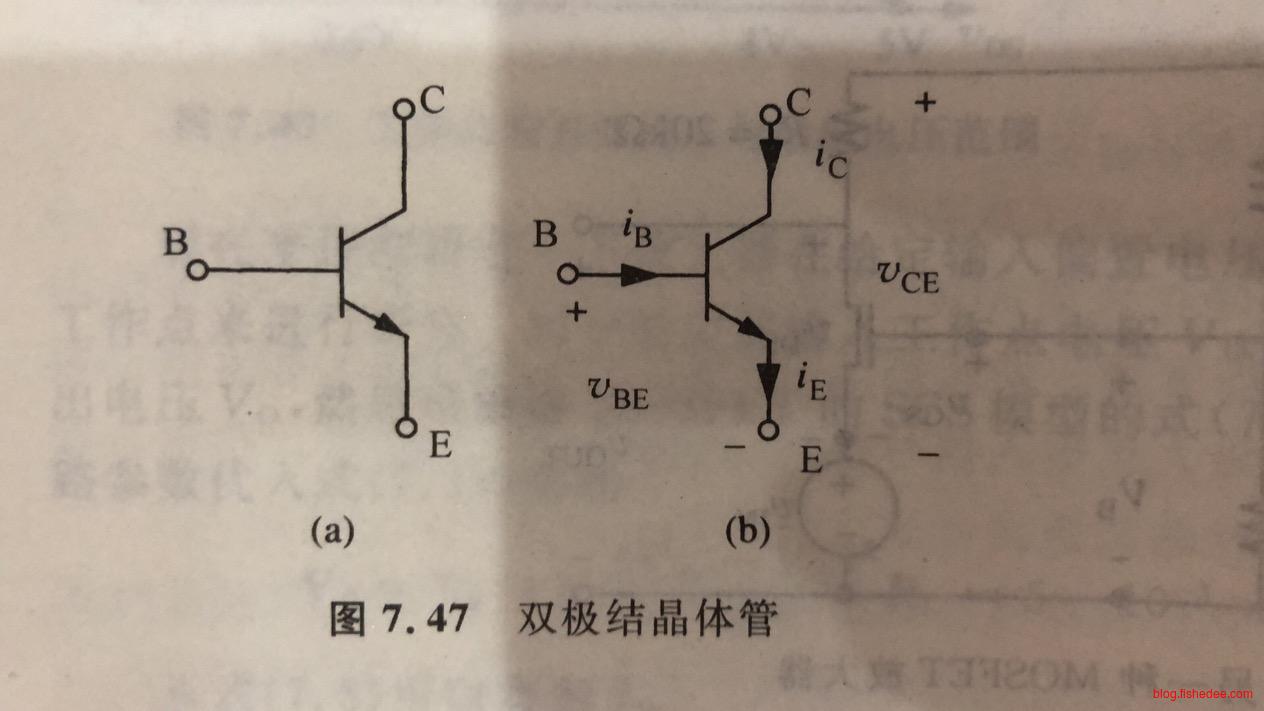
8.5 BJT模型
BJT是双极性晶体管,它和MOSFET一样,具有三个接线端,分别为基极B,集电极C和发射极E。
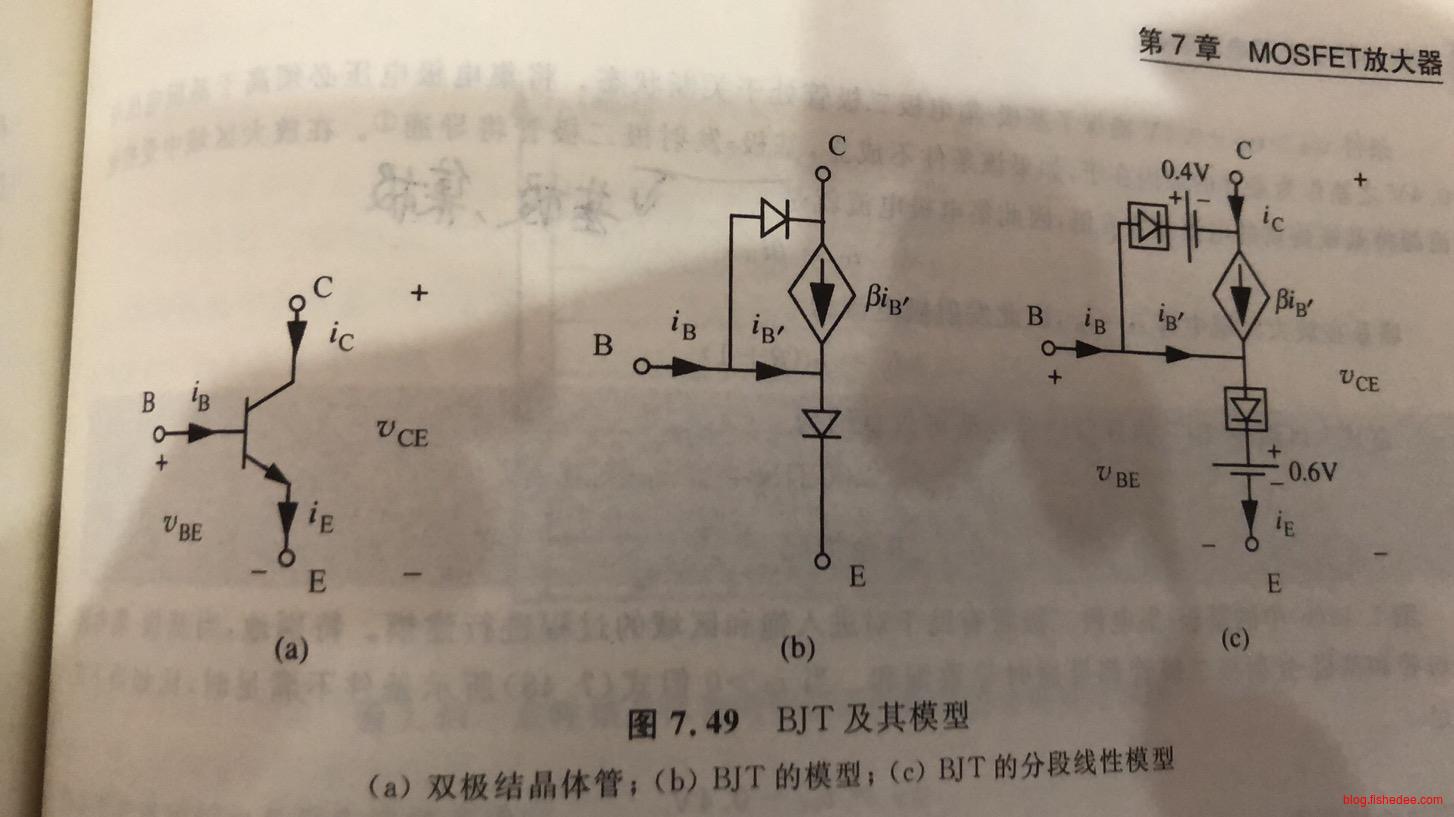
这是BJT的分段线性模型,它在三个区域中运行
- 当\(i_B>0\)且\(V_{BC}<0.4V\)时,BJT处于放大区域,BJT相当于一个流控电流源,\(i_C=\beta i_B\)。并且,这个时候\(V_{BE}=0.6V\)
- 当\(i_B=0\)时,BJT处于截止状态
- 当\(i_B>0\)且\(V_{BC}>0.4V\)时,BJT处于饱和区域,BJT相当于一个低电阻。并且,这个时候\(V_{BE}=0.6V\)且\(V_{BC}=0.4V\)
一般情况来说,我们要保证BJT一直运行在放大区域,避免运行在饱和区域,这和MOSFET的不同。
这是BJT三段模型的图形
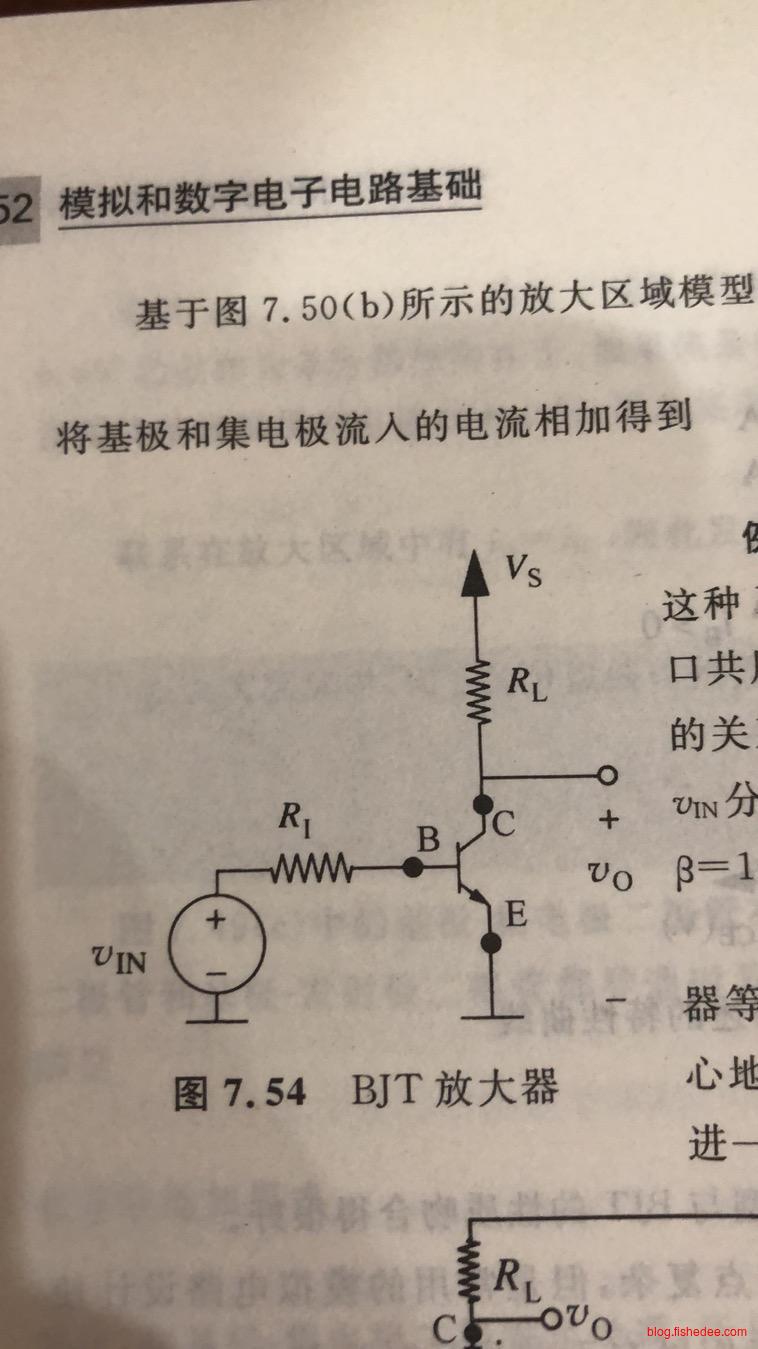
8.6 BJT放大器分析
8.6.1 电路
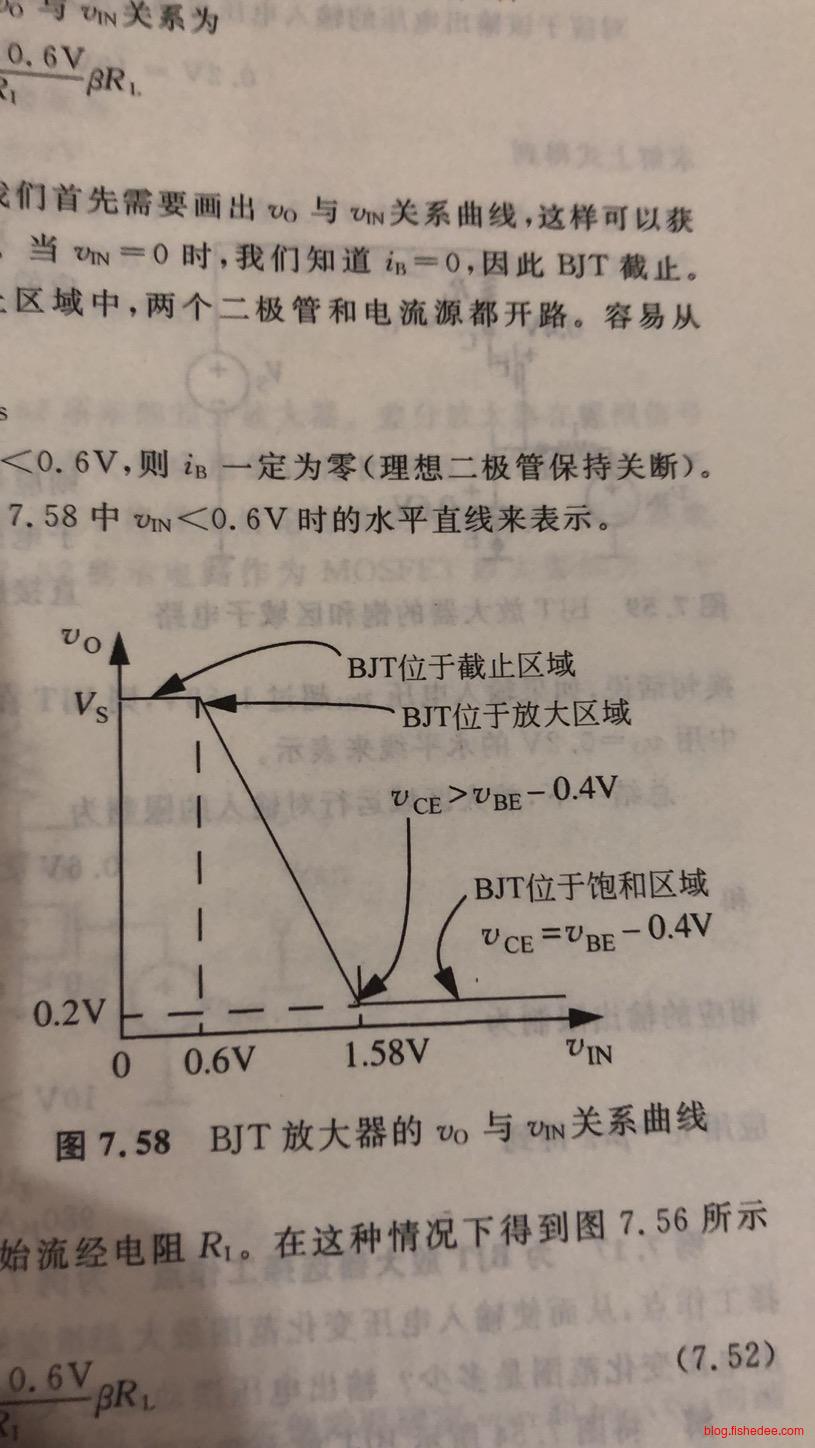
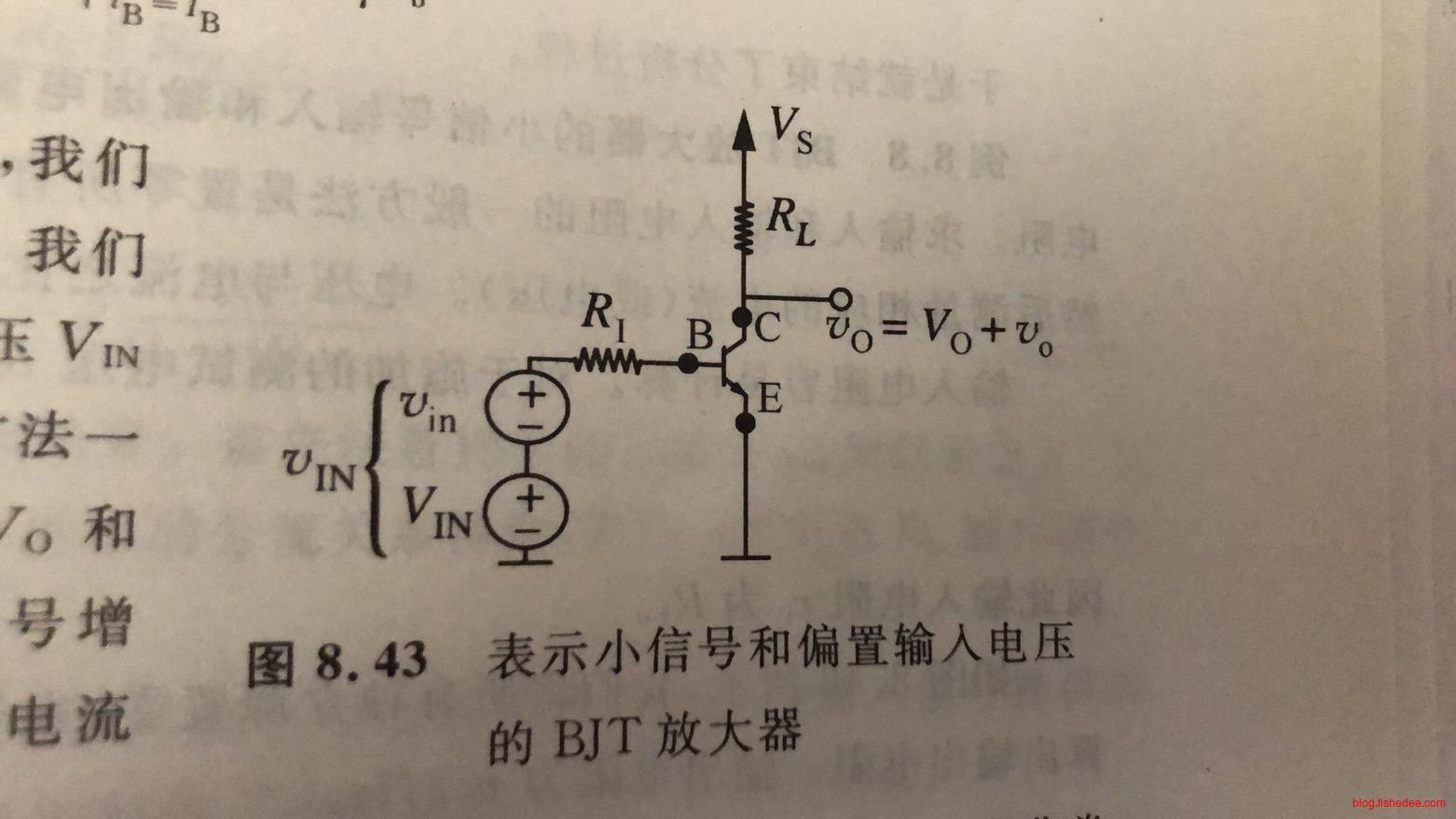
BJT放大器电路如上图所示,这个时候BJT一直运行在放大区域。并且,我们有:
\[ i_B = \frac {V_{IN}-0.6V} {R_1}\\ \frac {V_s-V_{OUT}}{R_L}=\beta i_B\\ \]
化简后得到:
\[ V_{OUT} = V_s - \frac {V_{IN}-0.6V} {R_1} \beta R_L \]
显然,这个电路为线性电路,并且是反向的
8.6.2 输入和输出范围
要让BJT正常工作,需要一直运行在放大区域,这意味着:
\[ \begin{cases} V_{IN}-0.6V >= 0\\ V_{BC} >= 0.4V\\ \end{cases}\\ \begin{cases} V_{IN}>= 0.6V\\ V_{CE}-V_{BE}>=0.4V\\ \end{cases}\\ \begin{cases} V_{IN}>= 0.6V\\ V_{OUT}>=0.2V\\ \end{cases}\\ \begin{cases} V_{IN}>= 0.6V\\ V_s - \frac {V_{IN}-0.6V} {R_1} \beta R_L>=0.2V\\ \end{cases} \]
化简后得到
\[ \begin{cases} V_{IN}>= 0.6V\\ V_{IN}<= \frac {R_L(V_s-0.2V)}{\beta R_L}+0.6V \end{cases} \]
输入电压工作范围为:
\[ 0.6V\to \frac {R_L(V_s-0.2V)}{\beta R_L}+0.6V \]
输出电压工作范围为:
\[ V_s \to 0.2V \]
8.6.3 偏移工作点
偏移工作点就是输入电压电压范围的中点,这点就不啰嗦了
8.7 差分放大器
8.7.1 普通电路
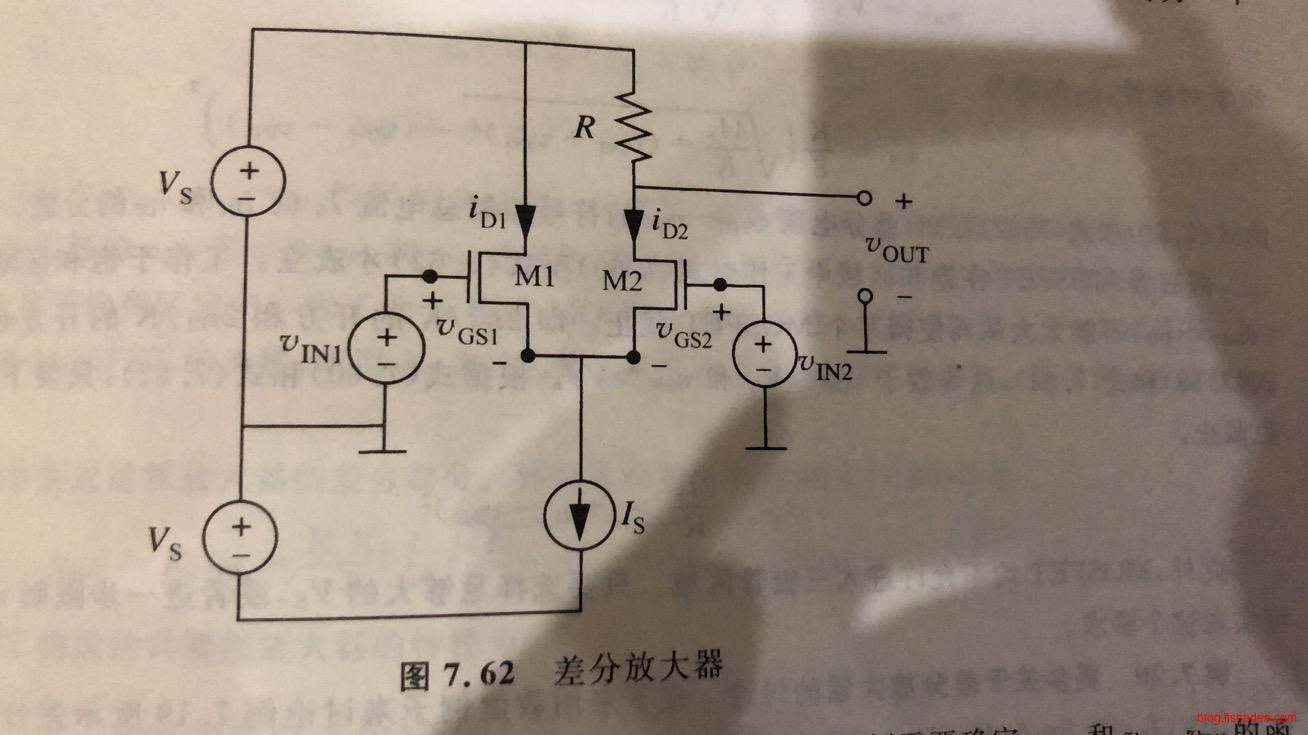
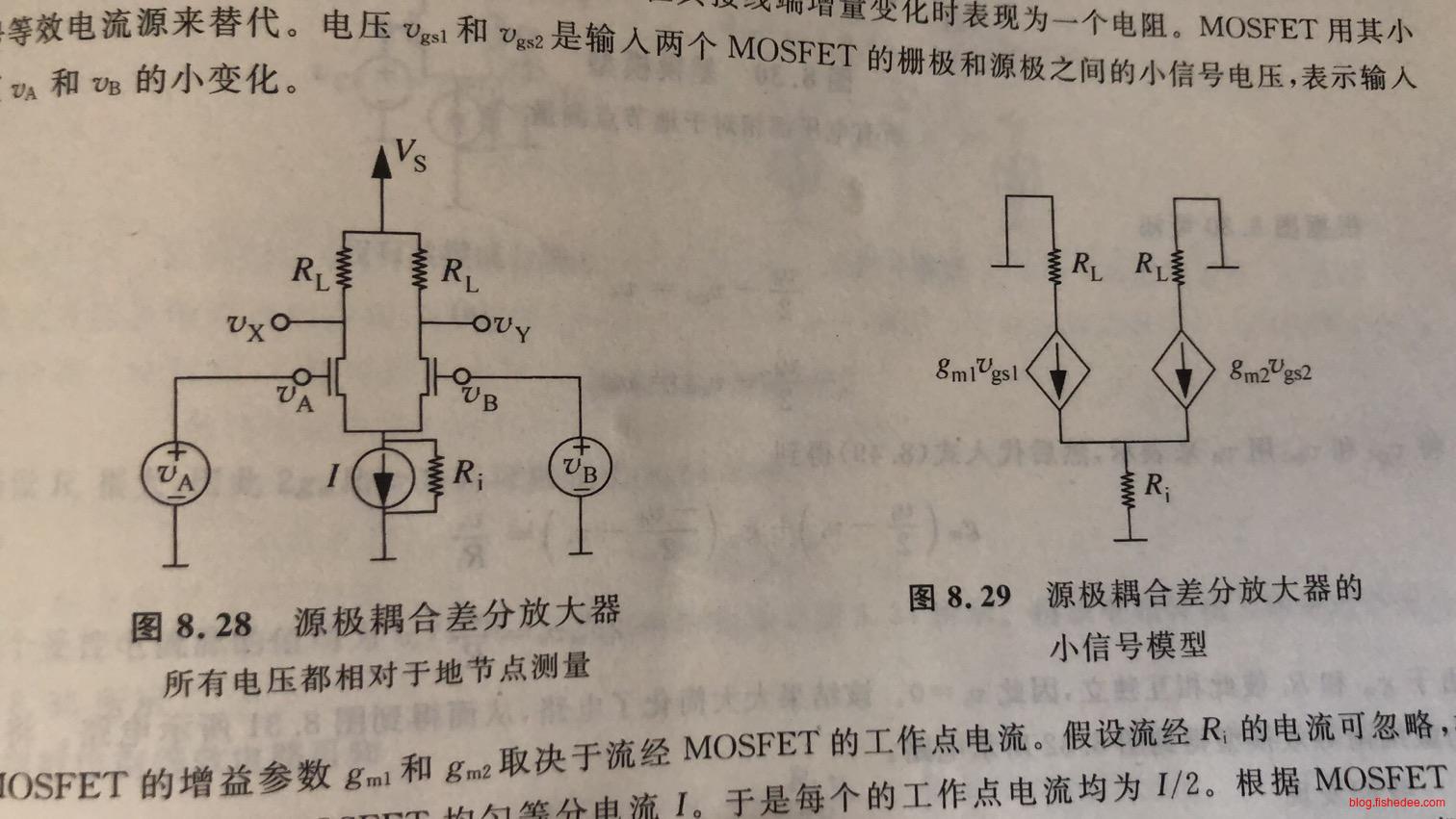
电路如上图所示,我们可以得出:
\[ i_{D1} = \frac {K}{2} (v_{GS1}-V_T)^2\\ i_{D2} = \frac {K} {2} (v_{GS2}-V_T)^2\\ i_{D1}+i_{D2} = I_s\\ v_{IN1} - v_{GS1} + v_{GS2} - v_{IN2} = 0\\ v_{OUT} = V_s - Ri_{D2} \]
化简得到:
\[ v_{OUT} = V_s - \frac {RK} {8}(\sqrt{\frac{4I_s}{K}-(v_{IN2}-v_{IN1})^2}-(v_{IN2}-v_{IN1}))^2 \]
显然,这是一个非线性电路,而且输出跟\((v_{IN2}-v_{IN1})^2\)有关,所以,这个电路称为差分放大器,它可以放大出两个输入端电压数值。不过,美中不足的是,这个电路是反向的,当差分是0的时候,输出反而是最大值。
8.7.2 共源极电路
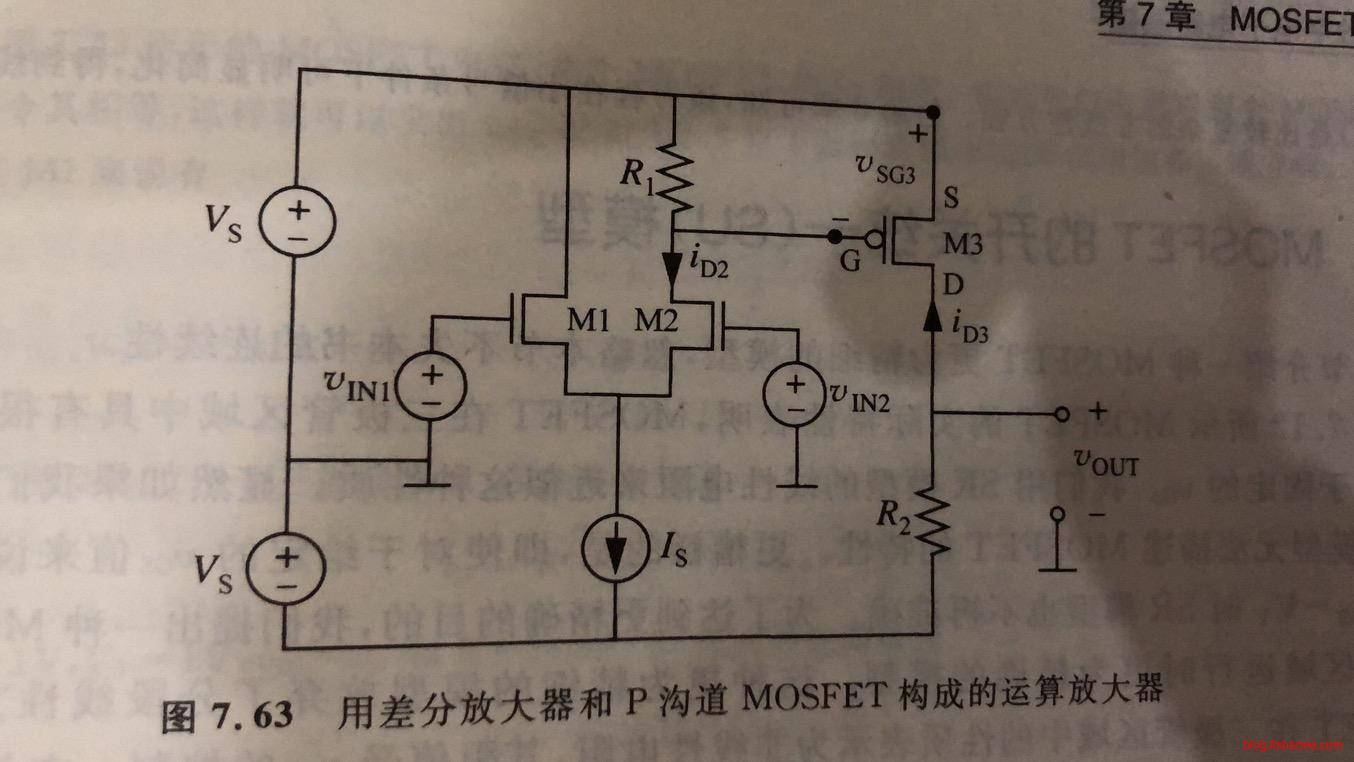
我们在普通电路的基础上,加入P沟通的MOSFET作为共源,然后取电阻两端电压作为输出。那么最后化简为:
\[ v_{OUT} = \frac {R_2K_P}{2}\{\frac{R_1K_N}{8}[\sqrt{\frac{4I_s}{K}-(v_{IN2}-v_{IN1})^2}-(v_{IN2}-v_{IN1})]^2+V_{TP}\}^2-V_s \]
那么,这个电路就很好地解决了这个问题,电路是正向的了。
8.9 SU模型
\[ i_{DS}=\begin{cases} K[(v_{GS}-V_T)v_{DS}-\frac {v_{DS}^2}{2}],v_{GS}\geq V_T且v_{DS}\lt v_{GS}-V_T\\ \frac {K(v_{GS}-V_T)^2}{2},v_{GS}\geq V_T且v_{DS}\geq v_{GS}-V_T\\ 0,v_{GS}\lt V_T \end{cases} \]
SU模型是统一开关模型,完整地描述了MOSFET在各个位置的特性,理论上比较完美,只是太复杂,实用性不太高。
9 MOSFET放大器小信号
9.1 小信号模型
9.1.1 出发点
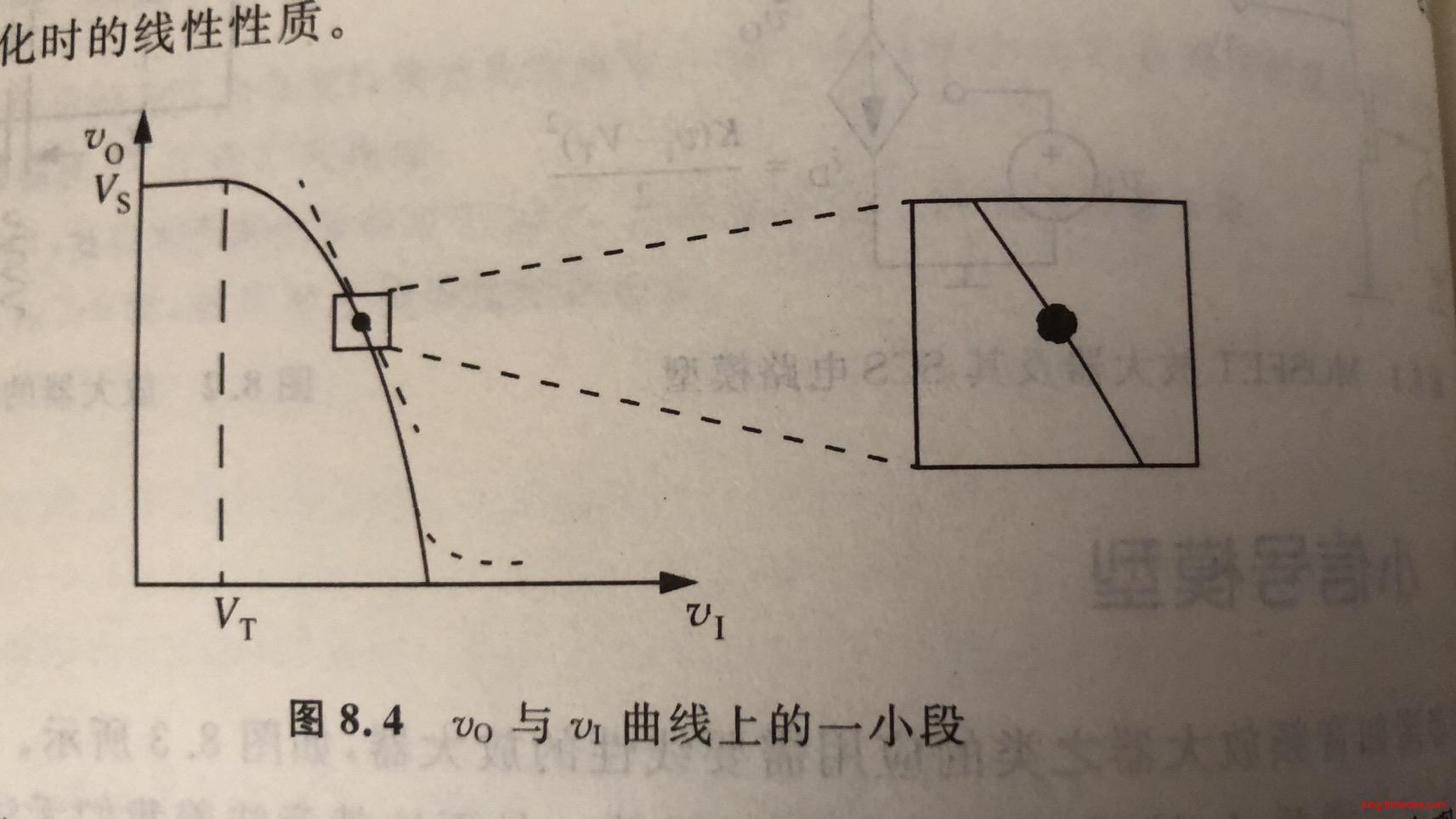
我们看到在绝大部分的放大器在都是非线性的,而我们需要的却总是需要线性放大的特性。解决办法是,我们让输入信号在一个大的偏置DC电压上运行,输入信号相对偏置DC电压来说幅度很小。
那么这个输入信号就可以看成是一个小信号,这个小信号在小曲线的一段上,它的输出与输入之间就可以近似为线性的。那么,我们下一步要做的是如何分析小信号的输出与输入的关系。
### 9.1.2 一般步骤
分析小信号模型的一般步骤为:
- 取每个电源值为工作点值,确定电路中每个元件支路电压和电流的工作点。
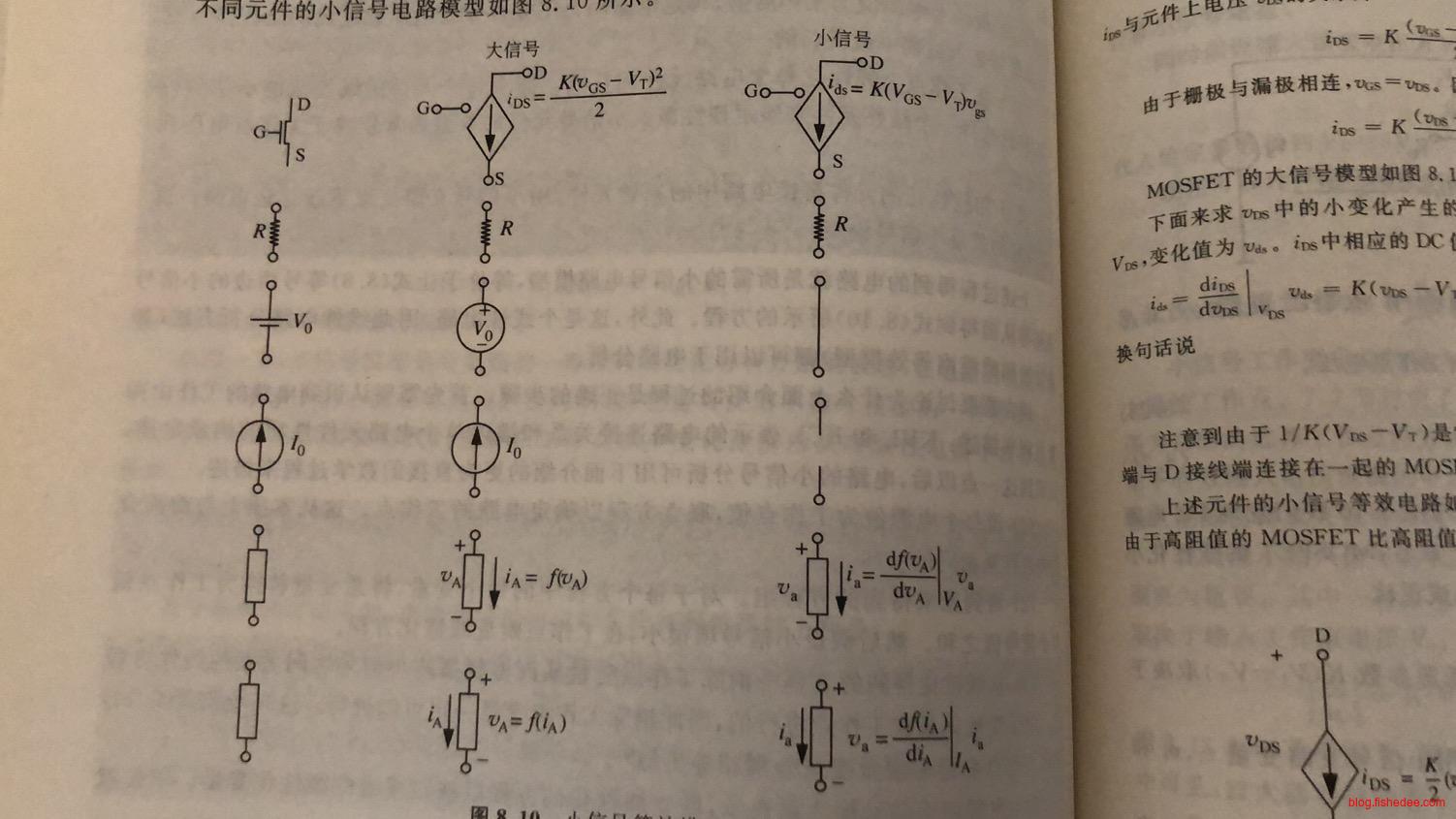
- 在工作点上线性化每个电路元件的性质。即求每个元件的线性化的小信号性质,然后选择一个线性元件来表示这个性质。小信号元件的参数通常依赖于工作点电压或电流。
- 用线性化的元件替换电路中的原始元件,用小信号支路变量重新标记电路。
这是不同元件的大小信号电路模型
### 9.1.3 输入电阻
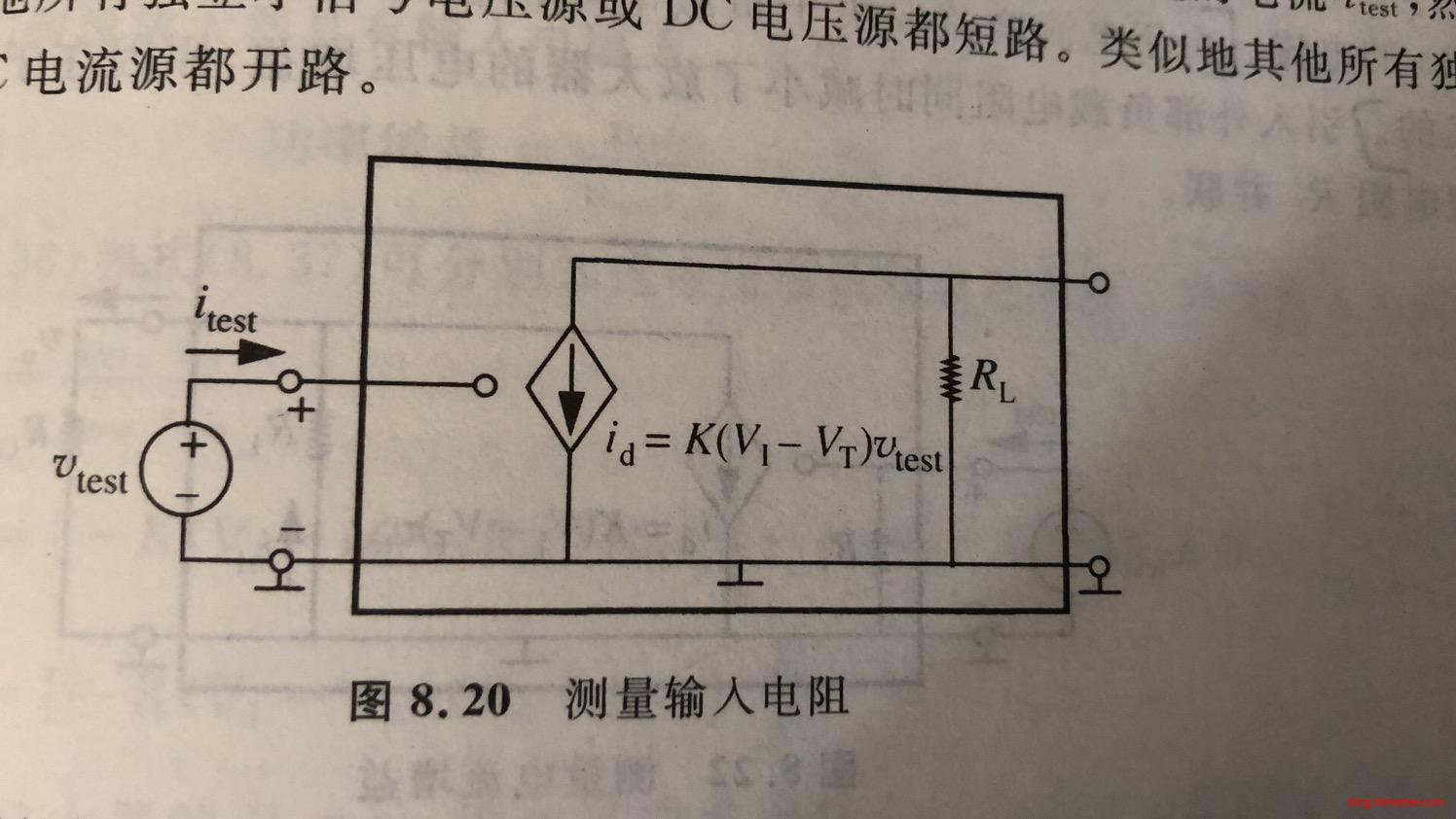
输入电阻\(r_i\),定义为输入电压变化与输入电流变化之比。常用的办法是,先将电路转换为小信号模型,然后在输入端指定输入\(v_{test}\)电压,测量或计算出输入电流\(i_{test}\),最后求它们的比值就可以了。
9.1.4 输出电阻
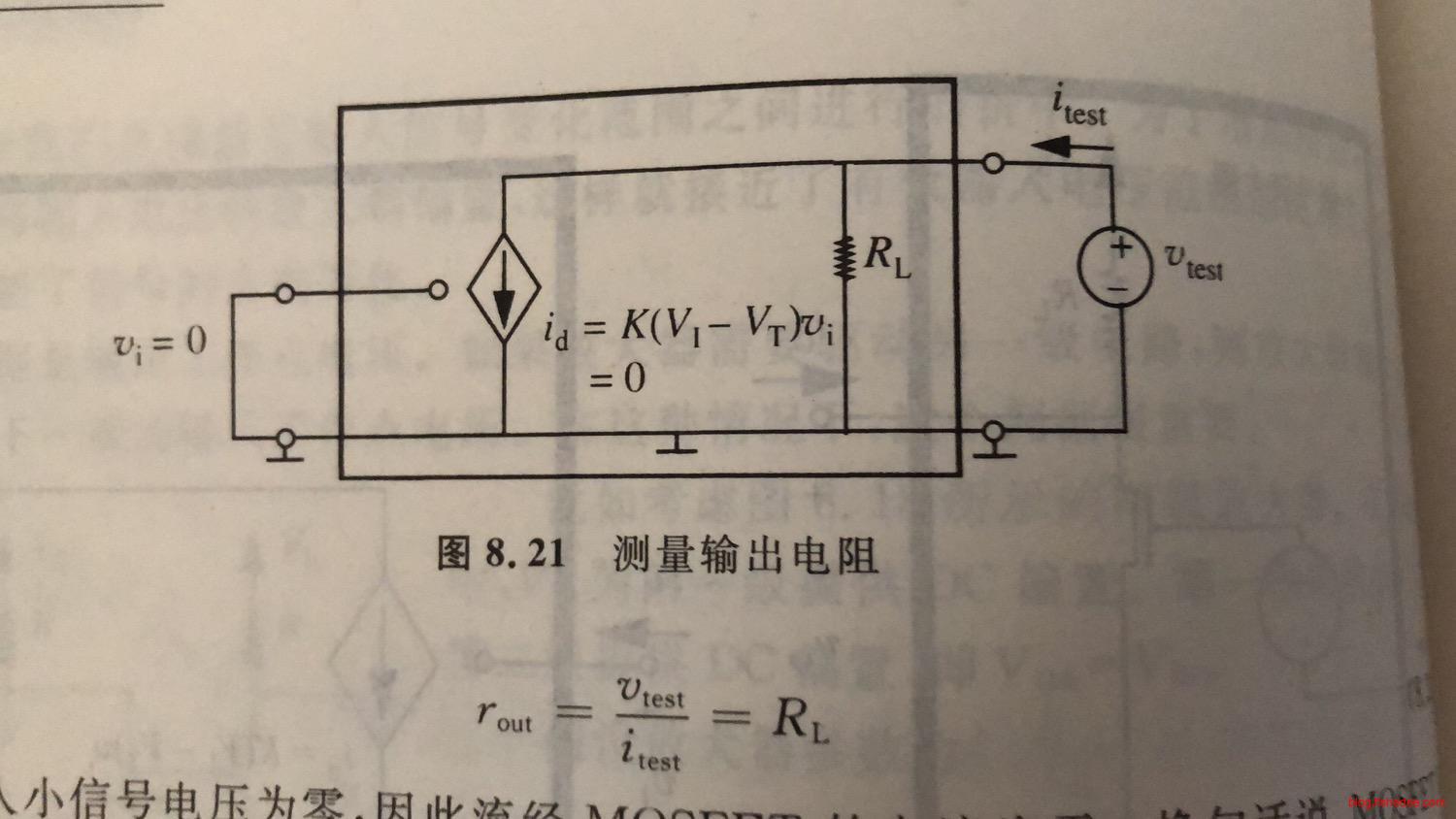
输出电阻\(r_{OUT}\),定义为输出电压变化与输出电流变化之比。注意,测试或计算的时候,输入电压必须为零。
9.1.5 电流增益
电流增益,定义为对于给定的外部负载电阻\(R_{O}\),输出电流与输入电流之比。注意,电流增益,必须在给定的负载电阻下计算或测量的。
9.1.6 功率增益
功率增益,定义为放大器向外部负载\(R_{O}\)提供的功率与输入信号向放大器提供的功率之比。
\[ 功率增益= \frac {v_Oi_O}{v_{test}i_{test}} = \frac {v_O} {v_{test}} \frac {i_O}{i_{test}} \]
9.2 MOSFET放大器
9.2.1 电路
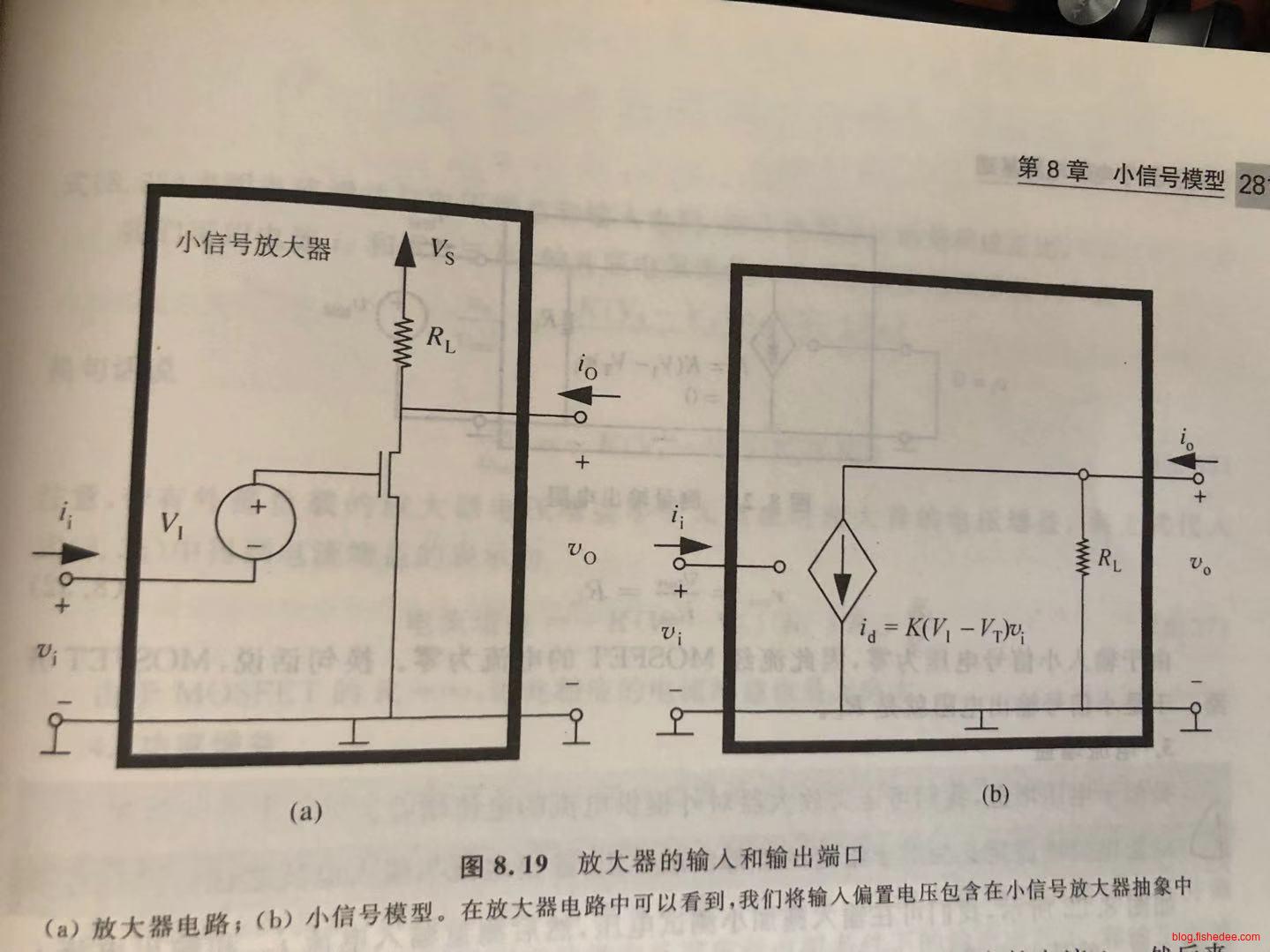
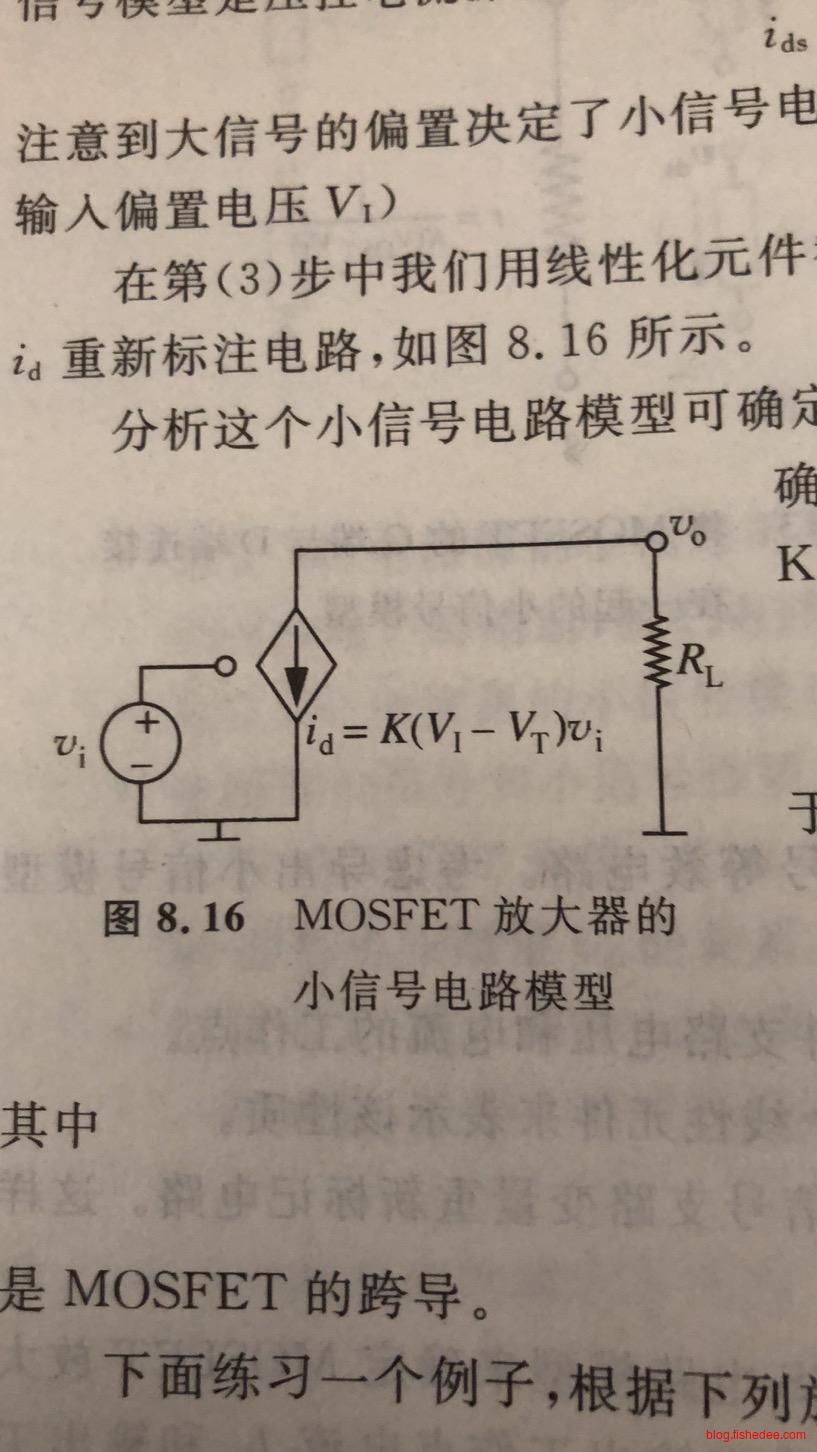
这是MOSFET放大器的电路,及其对应的小信号模型。注意,放大器位置被电阻化了,它的计算通过求导出来的。另外,电压源被置零,也就是短路了。
\[ i_D = \frac {K(v_I-V_T)^2} {2}\\ i_D' = K(v_I-V_T)\\ i_d = K(v_I-V_T)v_i\\ \]
这是MOSFET元件小信号模型的推导,注意,\(v_I\)是大信号的输入,也就是偏置电压。
\[ v_o = -i_dR_L = -K(V_I-V_T)v_iR_L\\ \frac {v_o} {v_i} = -K(v_I-V_T)R_L \]
因此,我们推导出了MOSFET放大器在小信号模型中的电压增益,就是\(-K(v_I-V_T)R_L\),这个增益与工作点的电压有关。在第8章的时候,我们认为工作点的选择应该取在输入范围的中点,但是在这一章,我们需要指出,工作点的选择还会和用户需要的电压增益有关。因此,我们指出:
- 工作点需要考虑到最大的小信号范围,工作点电压应该在输入范围的中点,这样小信号的可用范围最大。
- 工作点需要匹配用户需要的电压增益,MOSFET的工作点电压越大,增益越大。
- 工作点需要匹配下一级的输入电压,工作点电压会影响下一级的输入电压。
9.2.2 输入电阻
\[ r_i = \frac {v_{test}} {i_{test}} = \frac {v_{test}} {0} = \infty \]
MOSFET的输入总是没有电流通过,所以输入电阻为无穷大。
9.2.3 输出电阻
\[ r_{OUT} = \frac {v_{test}} {i_{test}} = R_L \]
由于输入的电压为零,所以输出方的测试电流,只流向\(R_L\),所以输出电阻为\(R_L\)
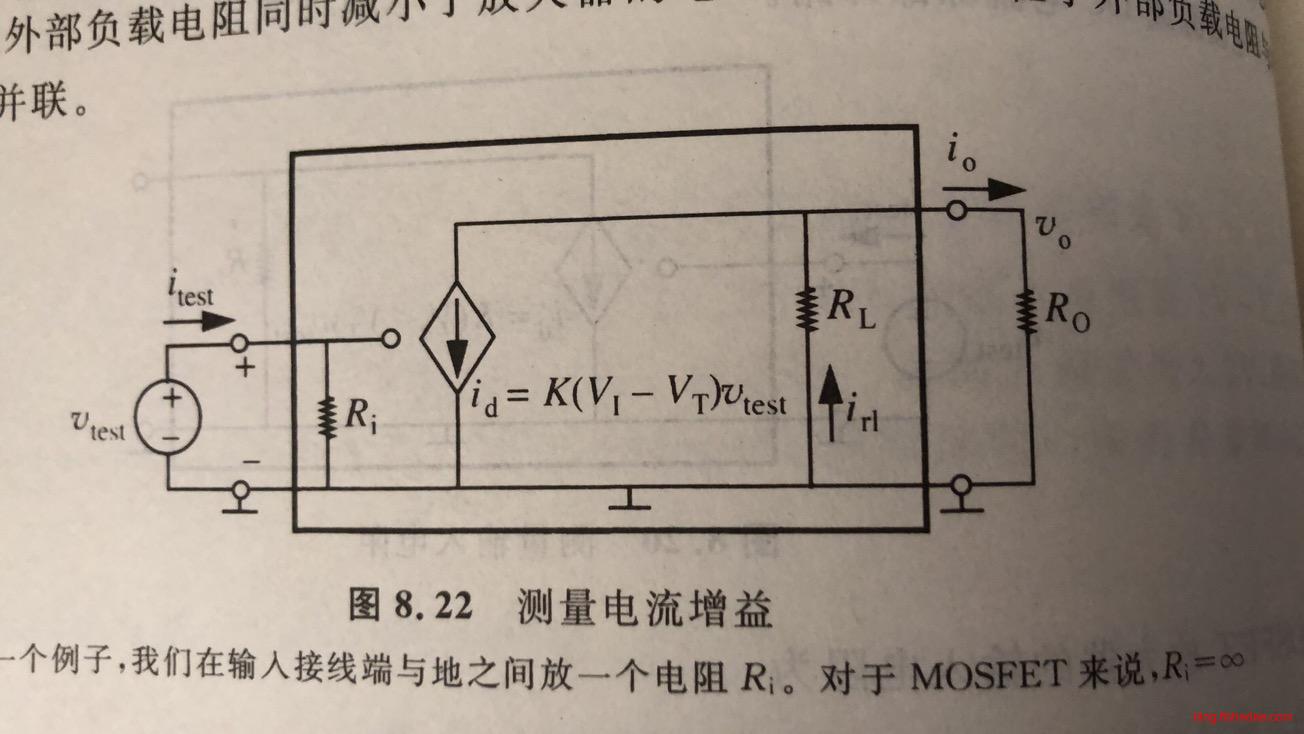
9.2.4 电流增益
\[ i_{test} = \frac {v_{test}}{R_i} \]
这是输入电流,\(R_i\)是MOSFET的GS端电阻,默认为无穷大
\[ i_{o} = -i_d\frac{R_O} {(R_L||R_O)} = -\frac {K(V_I-V_T)v_{test}R_O}{(R_L||R_O)} \]
这是给定负载电阻下的输出电阻
\[ \frac {i_{o}}{i_test} = -K(V_I-V_T)(R_L||R_O)\frac{R_i}{R_o} \]
从公式中可以看出,电流增益可以为无穷大
9.2.5 功率增益
\[ 功率增益= [-K(V_I-V_T)(R_L||R_O)]^2\frac{R_i}{R_o} \]
类似的算法可以得出功率增益
9.3 源极跟随的MOSFET放大器
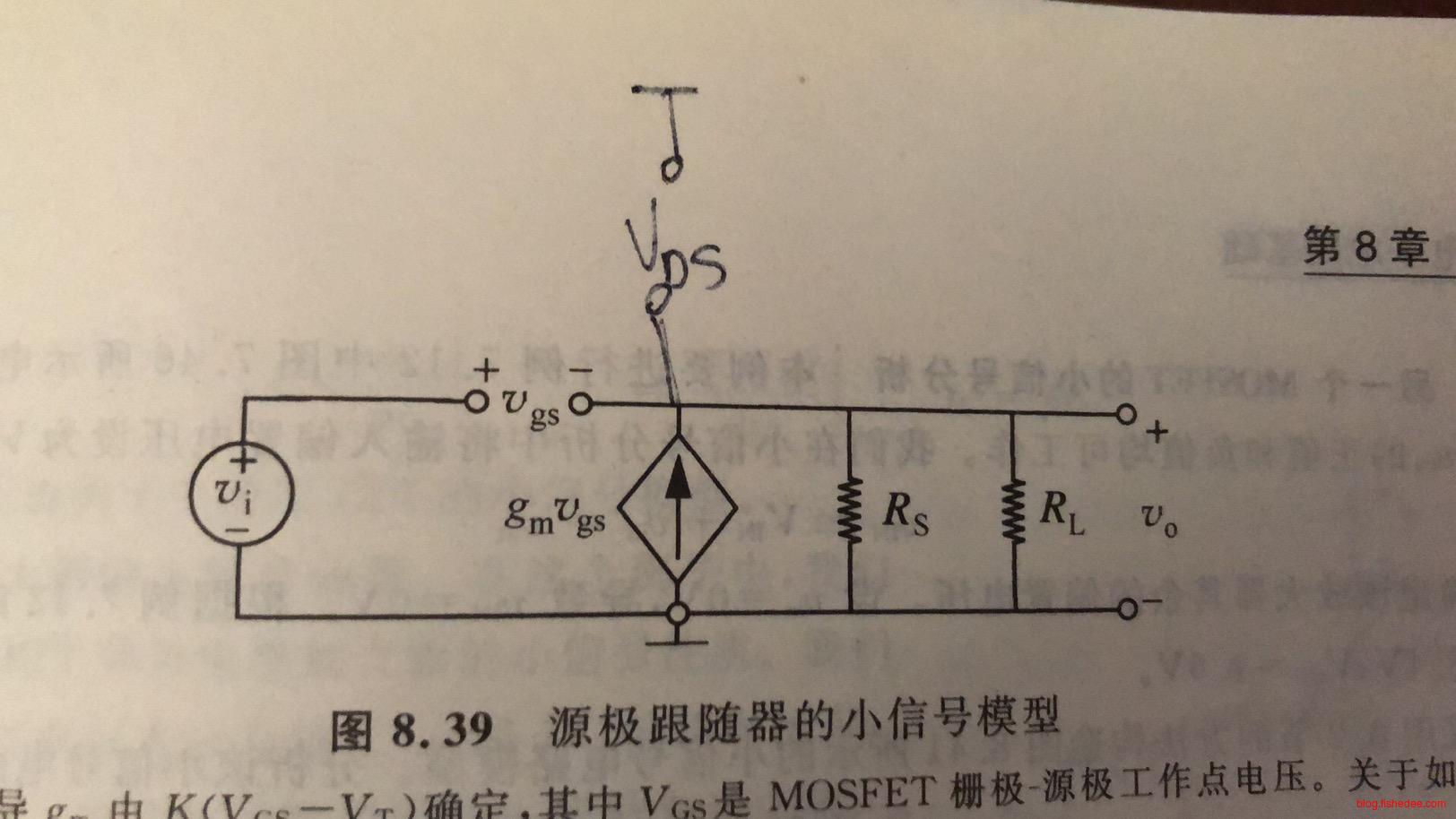
这是源极跟随的MOSFET放大器的小信号模型,我们可以得出
\[ v_o = g_mv_{GS}(R_L||R_S)\\ v_{GS} = v_i - v_o\\ \]
化简后得到
\[ \frac {v_o} {v_i} = \frac {R_LR_Sg_m}{R_L+R_S+R_LR_Sg_m} \]
电压增益如上,当\(R_L\)很大的时候,电压增益接近为1,小信号模型依然不是线性的。源极跟随MOSFET放大器特点是它的输出电阻很小,可以提供很大的电流增益。
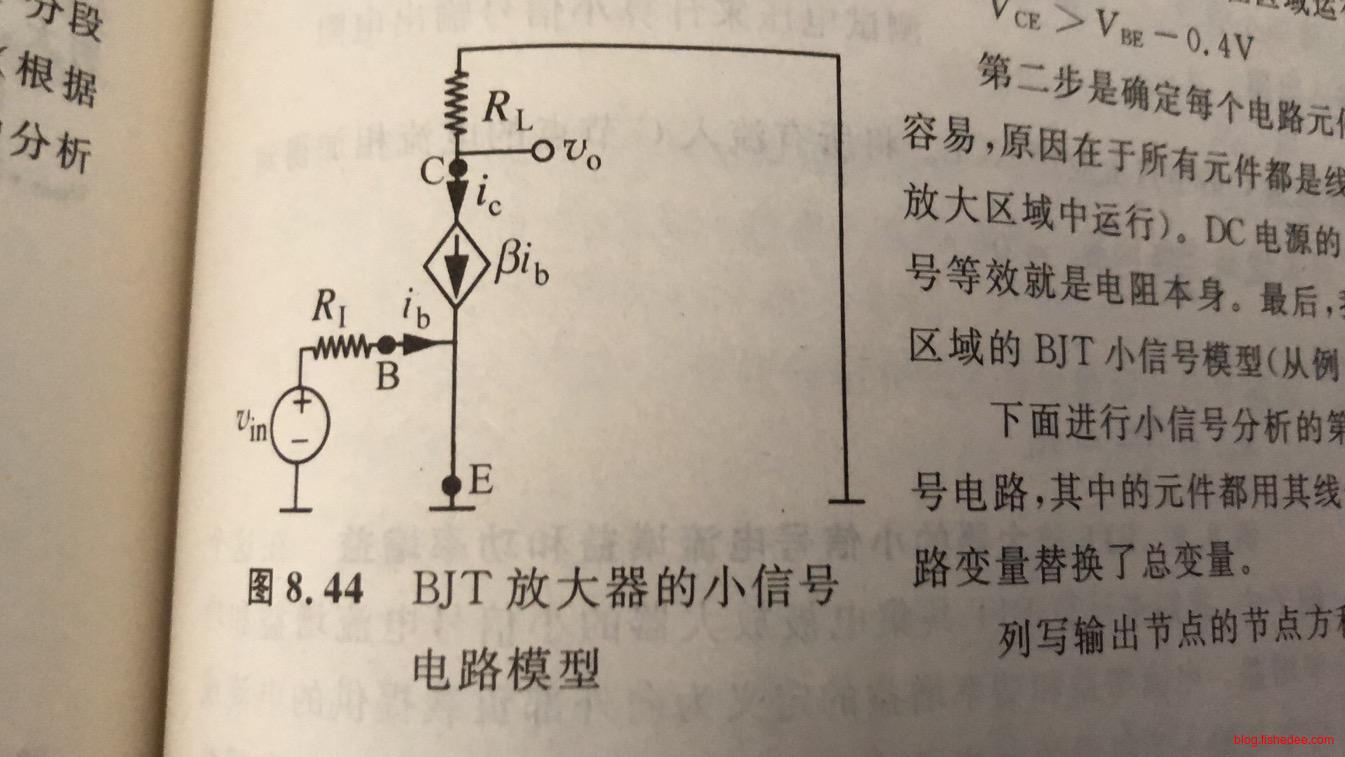
9.4 BJT放大器
这是BJT放大器的小信号模型
\[ i_C = \beta i_B\\ i_C' = \beta\\ i_c = \beta i_b\\ \]
以上是BJT模型的小信号模型推导,可以看出,它的模型与工作点无关,仅仅与BJT自身的\(\beta\)有关。
\[ \frac {v_o} {R_L} = -\beta i_b\\ i_b = \frac {v_{in}} {R_i}\\ \]
化简后得到
\[ \frac {v_o}{v_{in}} = -\beta \frac {R_L}{R_i} \]
这是BJT放大器的电压增益,可以看出,就是两个电阻的比例,所以很容易就能造成可调增益。
9.5 差分放大器
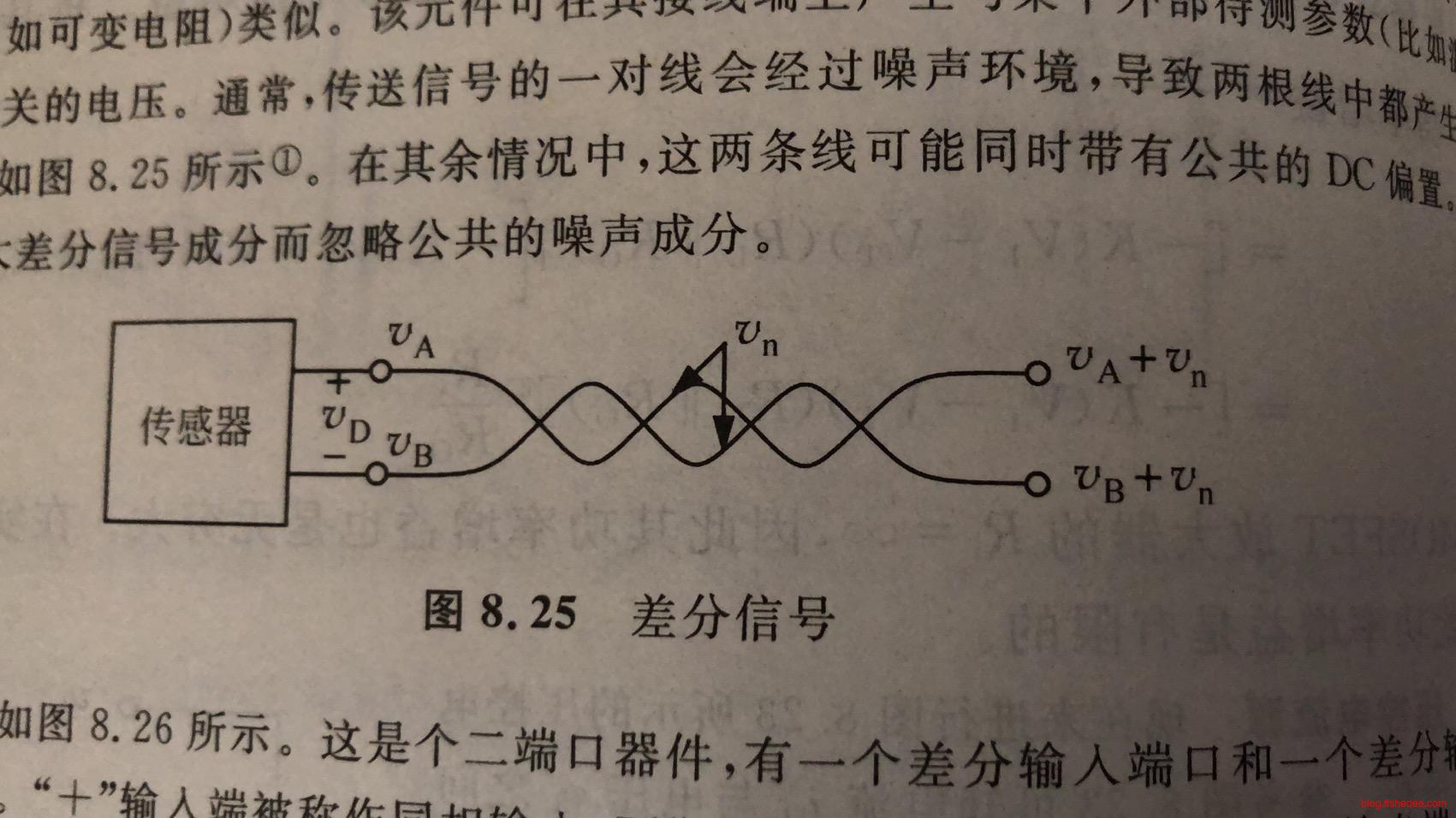
我们可以假设要从传感器中获取数据,传感器可以选择从一条线中输出电平,但是这样做很容易导致噪音让一条线变得受干扰。
更好的办法是,传感器在输出一个差分信号,也就是两条线输出信号。接受端收到双信号时,需要做一个差分操作,得到一个\(v_o\)就是结果。这样做的优势在于,当两条线互相缠绕在一起的时候,它们得到的干扰信号常常是相同的,一旦执行差分结果以后,噪音就会被去掉了。另外,传感器输出的时候,可以在\(v_B\)设计为单个正弦信号,而\(v_A\)就是为信号+正弦的叠加信号即可。
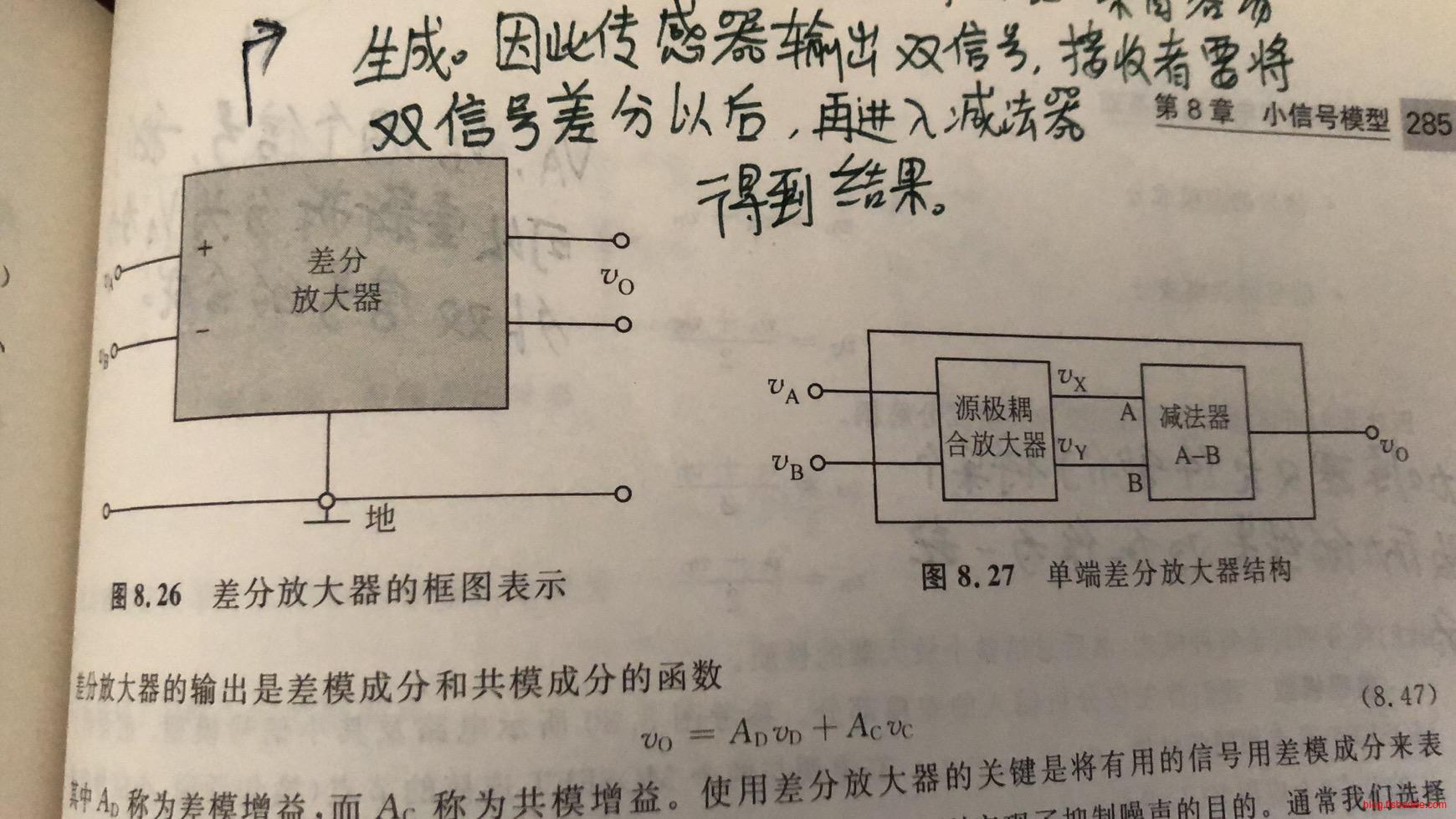
由于收到信号以后,要做差分操作,所以,两条线需要明确从哪条线信号减哪条线的信号。因此,我们定义,输入端口的+端为同相输入,-端为反相输入,接收器总是将同相输入减去反相输入得到结果的。
这是源极耦合的差分放大器的设计,由于\(v_A\)和\(v_B\)是未知的,但是在小信号模型中,电路是线性的,允许使用叠加原理的。因此,我们可以将\(v_A\)分解为两个信号的叠加,\(v_B\)也分解为两个信号的叠加。
\[ 差模信号:v_D = v_A-v_B\\ 共模信号:v_C = \frac {v_A+v_B}{2}\\ \]
我们先定义两个信号,差模和共模。
\[ v_A = \frac {v_C+v_D}{2}\\ v_B = \frac {v_C-V_D}{2}\\ \]
那么,我们就能将\(v_A\)分解为差模和共模信号的叠加,和\(v_B\)也分解为差模和共模信号的叠加。那么我们要求\(v_A\)和\(v_B\)在上述电路的输出是什么,我们可以分解为\(v_A\)中的差模和\(v_B\)的差模的输入结果,和\(v_A\)中的共模和\(v_B\)的共模的输入结果,的叠加。
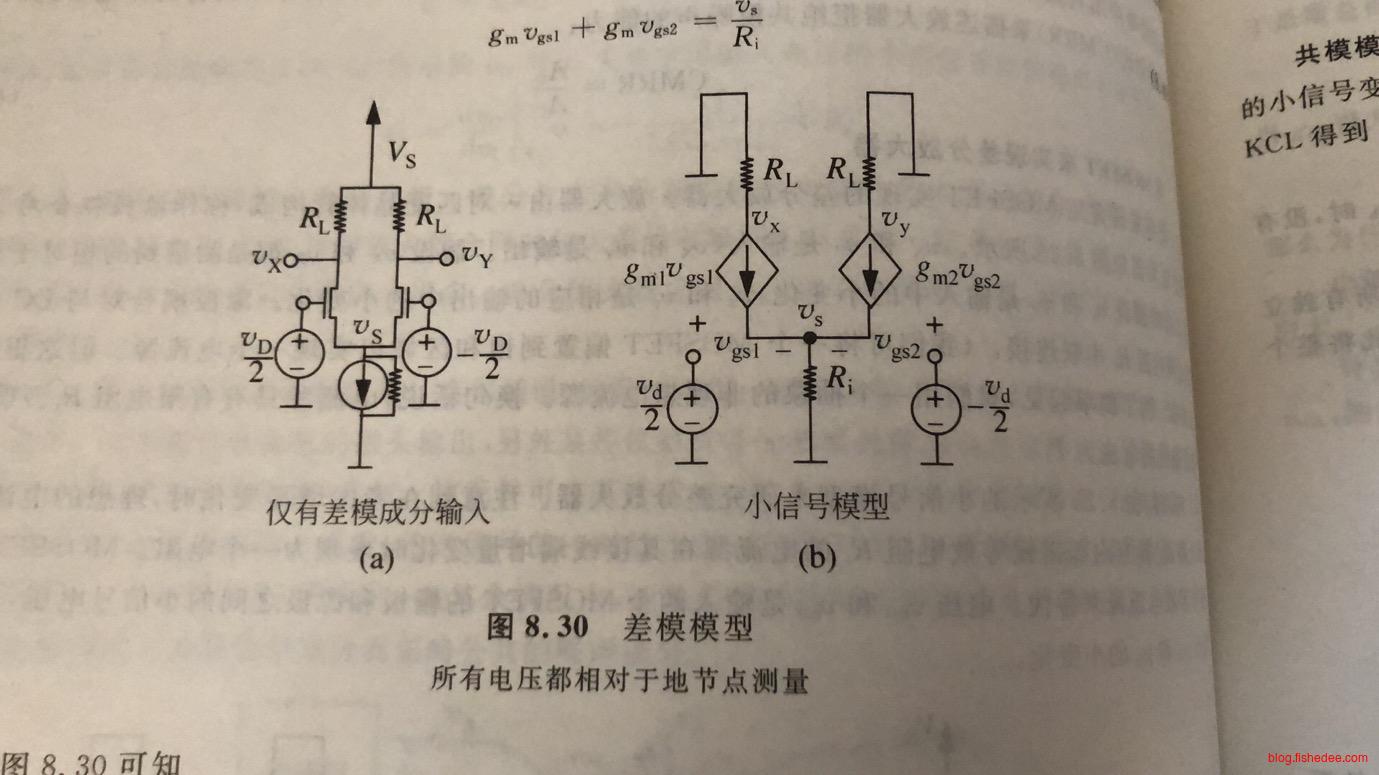
这是\(v_A\)中的差模和\(v_B\)的差模的输入的电路。
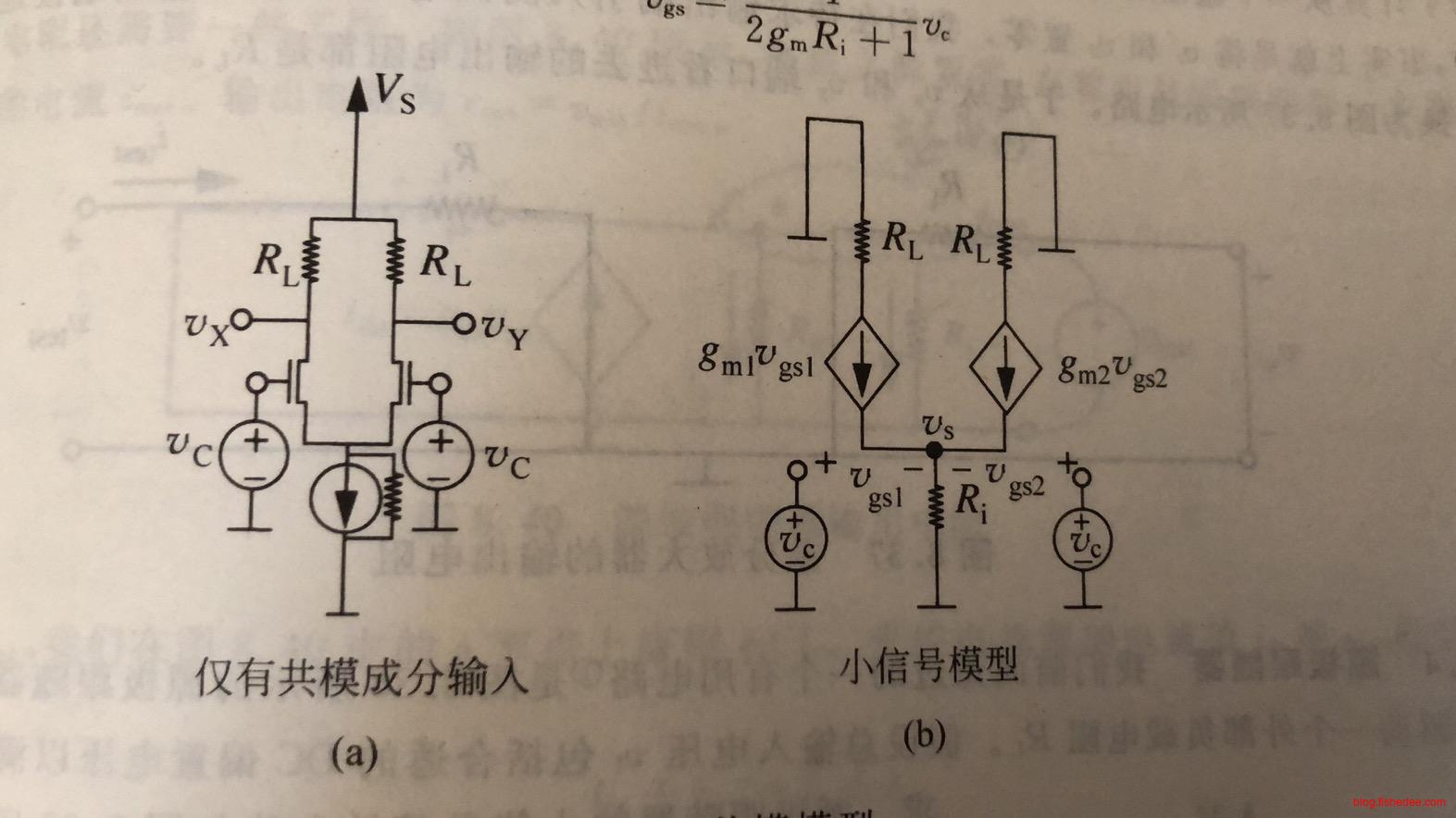
这是\(v_A\)中的共模和\(v_B\)的共模的输入的电路。
为什么要分成这两个电路,因为这样做能大大简化结果,而且还能分别计算出差模的增益和共模的增益是多少。
\[ CMR = \frac {A_D}{A_C} \]
共模抑噪比,就是描述放大器拒绝共模噪声的能力
- 本文作者: fishedee
- 版权声明: 本博客所有文章均采用 CC BY-NC-SA 3.0 CN 许可协议,转载必须注明出处!