PageRank模型

2017-10-08 fishedee 数学

1 概览

PageRank是一个相当简单的模型，解决了相互投票的评价问题。

2 问题

Google之前的搜索引擎是相当粗糙的，用户输入关键词以后，搜索引擎到数据库中寻找包含这个关键词的网页。问题是，A网页和B网页都包含了这个关键词，我怎么确定A网页的搜索结果更可靠，或者是B网页的搜索结果更可靠呢？当时Yahoo做法相当暴力，人工维护每个网站的权威性权重，例如，Yahoo网站的权重是10，某非主流博客的权重是1，那么根据关键词搜索出网页以后，就按照权威性权重进行从大到小的排序就可以了。很显然，这个方法太暴力了，当网页指数式递增时，人工维护权重的工作量就大到几乎不可能完成。

3 模型

一个很直观的想法，就是让机器理解网页的文本内容，看谁更贴合关键词的语义。很明显，这个方向搞不定，NLP处理直到现在都是前沿问题。就像协同过滤对推荐算法的想法一样，对权威性权重的获得我们可以通过网页之间的链接量来描述。例如，一个大型而且权威的网站它会常常被其他网站所指向。所以，我们可以通过网站的入链数来描述网站的权威性权重。

\[ x_i = 指向网站i的其他网站数目 \]

但是，这种方法太容易被操控了。我建立一个垃圾的A网站，然后让其他狐朋狗友也开网站来指向垃圾的A网站，那么A网站的入链数也很多呀，权威性权重就会虚高太多。所以，只用入链数来描述权威性权重是不行的。这样做的根本问题在于，权威性权重不仅需要考虑入链的数目，还要考虑入链的质量。也就说，垃圾网站的出链的网站很有可能也是垃圾，优质网站的出链更有可能是优质网站。用数学表达式表示就是：

\[ x_i = p_{i1}x_1+p_{i2}x_2+...+p_{in}x_n \]

其中\(p_{i1}\)是\(x_1\)的出链数目的倒数，也就是说，\(x_1\)有10个出链，而\(x_1\)本身的权重是1的话，那么\(p_{i1}x_1\)就是等于0.1，代表\(x_1\)每个出链的价值。用矩阵表示，就是

\[ AX = X \]

其中A是各个网站之间的出链权重矩阵，然后我们的目标就是求解X，并且，\(\sum X=1\)，即所有网站的权威性权重总和为1。直接求解这个方程组是比较困难的，因为这个矩阵实在太大了，1w个网站时，这个矩阵就有1亿个元素，求解X相当困难。

PageRank算法不仅建立了模型，还给出了求解的方法。它发现，当矩阵A满足:

  • stochastic matrix，即每个行至少存在一个非零值，也就是必须存在一个外链接
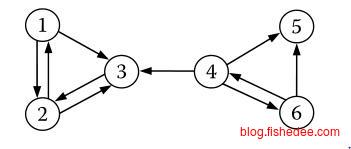
  • 不可约（irreducible），即矩阵A所对应的有向图G必须是强连通的，对于任意两个节点u,v∈V,存在一个从u到v的路径；
  • 非周期性（aperiodic），即每个节点存在自回路。

用大白话来说，就是每个网站都有出链，而且出链之后都能去到任意一个其他网站，包括能回到自己，那么，我们可以使用下面的方法迭代求解这个X。

  • 任意确定当前的解\(X_i\)
  • 计算\(X_{i+1}=AX_{i}\)，以\(X_{i+1}\)作为\(X\)的进一步近似求解。
  • \(X_{i}=X_{i+1}\)，返回到上一步

也就是使用\(\lim\limits_{n\to \infty}AX_0\)作为X的解，一般迭代10次左右就能收敛了，而且PageRank证明了对于任意初始化的\(X_0\)，结果都能收敛。

\[ AX = X \]

另外，当A矩阵不是很大时，X可以看成是矩阵A的特征值为1的特征变量，那么可以通过求解矩阵A的特征向量就可以了。

4 优化

PageRank的原始模型中对矩阵A的要求过于苛刻了，并不是所有网站都有出链的，总有些自私的网站没有出链，也总有些网站只在自己的圈子里互相链接，而不指向出去。所以，为了解决这个问题，PageRank加入了阻尼系数e，代表每个网站都有一定的概率e跳转到其他网站去，而每个网站也有\(e/N\)的权重是来自于其他网站的。那么，权重表达式为：

\[ x_i = (1-e)(p_{i1}x_1+p_{i2}x_2+...+p_{in}x_n)+\frac {e} {N} \]

那么，矩阵形式为：

\[ X = (1-e)AX +\frac {e} {N}1 \]

其中1代表Nx1向量，由于X的列和为1，也就有\[1_{N\times N}X=1_{N\times N}\]，所以

\[ X = (1-e)AX +\frac {e} {N}1\\ X = (1-e)AX +\frac {e} {N}1_{N \times N}X\\ X = ((1-e)A +\frac {e} {N}1_{N \times N})X\\ 令U = ((1-e)A +\frac {e} {N}1_{N \times N})\\ 因此X = UX \]

显然，这个时候的矩阵U满足幂迭代法的要求，所以故技重施，用幂迭代法就能求出X了。

\[ X = (1-e)AX +\frac {e} {N}1\\ X-(1-e)AX = \frac {e} {N}1\\ (I-(1-e)A)X=\frac {e} {N}1\\ X = (I-(1-e)A)^{-1}\frac {e} {N}1 \]

当矩阵A不是很大时，我们可以用矩阵逆运算的方式求解出这个X。在实践中，阻尼系数设置为0.15之间效果最好。

5 总结

PageRank的模型最终被归根到一个\(X=UX\)的方程组求解问题上，模型相当简洁漂亮。最让人深刻的是，它用链接来评价网页的权威性，而不是网页的内容。这种方法就像协同过滤用人与物的关系来挖掘物品之间的相似度，而不是用物品的内容。根据这个算法的思路，我们可以轻易地迁移到，根据论文之间的相互引用情况来计算论文的权威程度，根据微博用户之间的关注关系来计算微博大V的流行程度，也就是一切根据相互投票来决定评价得分的问题我们都能用这个算法来解决。

当然，PageRank算法也不是万能，它虽然是Google发家时的看家本领，但是Google后来也扔掉它了，改用其他的衍生算法了。它的问题主要在于：

  • 没有主题敏感性，A网站的信息技术方面权威性比较高，B网站的娱乐新闻的权威性比较高，仅仅通过网站的总体权威性，不考虑关键词与网站之间的主题匹配度是不太准确的。
  • 对新网页不友好，新网页即使自身的质量非常好，但是缺少入链时就会排名比较排后了。
  • 没有区分链接自身的质量，指向自身的链接价值应该比较低，而指向广告的链接价值也应该低一点。

相关文章