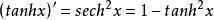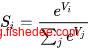1 概述
深度学习入门实现，简单地从零开始实现多层神经网络，以及卷积神经网络，以概览地了解深度学习的细节。注意，在整个实现的过程中没有涉及到gpu加速，只有cpu计算的版本。在此之前，你最好先了解《深度学习概览》中的内容。
在文章的末尾，我们将会使用我们自己开发的简陋的深度学习框架来识别手写数字，也就是入门的mnist数据集。
2 线性回归(LR)
2.1 模型
\[ y = w^Tx+b \]
线性回归是假设数据满足以上的线性假设，其中w和x是一个向量，y和b是一个实数。
\[ y = w_1x_1+w_2x_2+...w_nx_n+b \]
跟以上这个方程式是等价的。
\[ loss = \sum_{i=1}^{n}(y_i-\hat{y}_i)^2=\sum_{i=1}^{n}(w^Tx_i+b-\hat{y_i})^2 \]
显然，我们事先是不知道w和b取什么值是最好的。但是，我们知道，如果定义一个损失函数（就是上面的这个公式），当取到的w和b，使得损失函数的值最少时，这个w和b就是最好的。换句话说，当我们手上有足够多的一堆\((\vec{x_1},y_1),(\vec{x_2},y_2)...\)的事先已经标注好的数据时，我们就能通过损失函数来寻找到\(\vec{w},b\)。就这样，我们将一个学习问题，转化为一个优化问题。
很明显的，这个线性回归的问题在高中就已经研究过了，当时使用的是最小二乘法，但我们现在要使用的是梯度下降方法bgd。这种方法可谓是所有优化方法中最基本的一个，适用场景非常广泛，而且实现也很简单。到目前为止，深度学习的主流方法依然是离不开梯度下降，其他优化算法也只是梯度下降的变种而已。
2.2 梯度下降(bgd)
让我们先将线性回归的问题再简化一下，假设x只是一个实数，有没有偏置，也就是说\(y=wx\)
\[ loss = \sum_{i=1}^{n}(y_i-\hat{y}_i)^2=\sum_{i=1}^{n}(wx_i-\hat{y_i})^2 \]
那么loss函数就会是这个，很显然，公式中的\(x_i,\hat{y_i}\)都是常数，只有w是未知变量，那么loss就是一个关于w的二次函数而已。我们要求loss的最小值时的w，相当于求二次函数的最低点。
高中的方法就是一步到位，直接算出二次函数中导数为0的点，这个点就是最小值点。
梯度下降的方法是，首先，任意取一点w，然后算出该点w的导数，如果导数大于0，那就往w轴的负方向走，如果导数少于0，那就往w轴的正方向走。那么经过多步迭代后，我们总能走到最值点的附近。
\[ loss'(w) = 2\sum_{i=1}^{n}(wx_i-\hat{y_i})x_i\\ w^{n+1}=w^{n}-\eta loss'(w) \]
也就是上面的这条公式，任意取一个点w，然后计算w的导数\(loss'(w)\)，然后根据学习率\(\eta\)与导数相乘，就能得到新的一点w了。
\[ y = w^Tx+b\\ loss = \sum_{i=1}^{n}(y_i-\hat{y}_i)^2=\sum_{i=1}^{n}(w^Tx_i+b-\hat{y_i})^2 \]
那么，线性回归中，我们的想法也差不多，只不过就是需要调整的变量w不是一个，而是多个而已。这个时候，我们只需要依然画葫芦，只不过用的不是导数，而是偏导数而已。
\[ \frac {\partial loss} {\partial w_1} = 2\sum_{i=1}^{n}(wx_i-\hat{y_i})x_{i1}\\ w_1^{n+1}=w_1^{n}-\eta \frac {\partial loss} {\partial w_1}\\ \frac {\partial loss} {\partial w_2} = 2\sum_{i=1}^{n}(wx_i-\hat{y_i})x_{i2}\\ w_2^{n+1}=w_2^{n}-\eta \frac {\partial loss} {\partial w_2}\\ ...\\ \frac {\partial loss} {\partial b} = 2\sum_{i=1}^{n}(wx_i-\hat{y_i})\\ b^{n+1}=b^{n}-\eta \frac {\partial loss} {\partial b}\\ \]
以此类推，就可以了，就这么简单。代码在这里
2.3 随机梯度下降(sgd)
bgd的方法简单暴力，但是调整速度比较慢，随机梯度下降的想法就是，我不想等所有数据都计算完了才开始调整w，而是计算完数据的一部分(batch_size)后就立即调整w。
就这么简单，收敛速度更快，而且避免过拟合的问题。代码在这里
2.4 动量梯度下降(momentum)
嫌随机梯度下降的方法还不够快，没事，大神跳出来说还有动量梯度下降的方法。
\[ w = w - \eta \times g \]
普通的梯度方法，每次调整，都是梯度乘以学习率
\[ lg = lg \times discount +g\\ w = w - \eta \times lg \]
动量梯度下降的方法，从公式就可以看出，这次的梯度更新不仅考虑了当前的梯度，还考虑了以前的梯度，discount一般设置为0.9。
实践证明，动量梯度下降收敛速度真是快得可怕，代码在这里
2.5 Nesterov梯度下降(nesterov)
没有最可怕，只有更可怕，大神再次提出nesterov梯度下降的方法。它认为，即使当前的梯度为0，由于动量的存在，更新梯度依然会存在并继续更新w。
所以，继续当前点w的梯度是不太有意义的，有意义的是，假设下一个点w（仅靠动量滚到下一个点的w）的梯度方向才是决定当前梯度的重要因素。举个通俗的例子就是，你在下坡时，如果在下坡快到底，但又未到底时，动量梯度下降会让你冲到坡的对面去。Nesterov梯度下降会预知你的下一步将会时到坡的对面去，所以会提示你提前刹车，避免过度冲到坡的对面去。这包含了一种提前计算下一步的梯度，来指导当前梯度的想法。
\[ oldw = w\\ w = w - \eta \times lg \times discount\\ 计算w下的梯度g\\ w = oldw\\ lg = lg \times discount +g\\ w = w - \eta \times lg \]
实践证明，Nesterov梯度下降太吓坏人了，快得疯了，代码在这里
最后是，梯度下降算法中严重依赖于学习率\(\eta\)的设置，学习率\(\eta\)太大，收敛不到最值点，\(\eta\)太小，收敛速度过慢。所以，大神继续提出不需要配置\(\eta\)的方法，分别是adadelta，adam，rmsprop等等。
3 逻辑回归(LR)
3.1 模型
\[ z = w^Tx+b\\ y = \frac {1} {1+e^{-z}} \]
\[ loss = \sum_{i=1}^{n}(y_i-\hat{y}_i)^2=\sum_{i=1}^{n}(w^Tx_i+b-\hat{y_i})^2 \]
逻辑回归，就是在线性回归的基础上加入了sigmoid的输出函数，sigmoid就是一个将输出映射到[0,1]之间的函数了。依然，是一样，我们需要的是计算loss对各个w和b的偏导数就可以了。
\[ \frac {\partial loss} {\partial w_1} = \frac {\partial loss} {\partial y} \frac {\partial y} {\partial z}\frac{\partial z} {\partial w_1}\\ \frac {\partial loss} {\partial y} = 2\sum_{i=1}^{n}(y_i-\hat{y}_i)\\ \frac {\partial y} {\partial z}=\frac {e^{-z}} {(1+e^{-z})^2}\\ \frac {\partial z} {\partial w_1} = x_1 \]
也就是说
\[ \frac {\partial loss} {\partial w_1} = 2\sum_{i=1}^{n}(y_i-\hat{y}_i)\frac {e^{-z}} {(1+e^{-z})^2}x_1 \]
相当于在原来线性回归的基础上，插入多一个sigmoid的梯度而已。注意，这里的偏导数计算使用的是复合导数计算的链式法则。
那么，问题就很简单了，在线性回归的代码上，加入sigmoid的梯度计算就可以了，代码在这里
逻辑回归的方法相当于在一个神经元的基础上加入了一个sigmoid的激活函数。
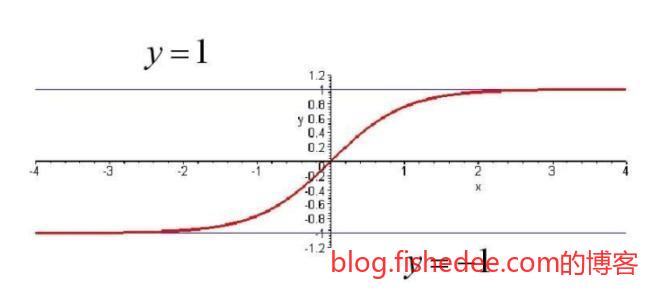
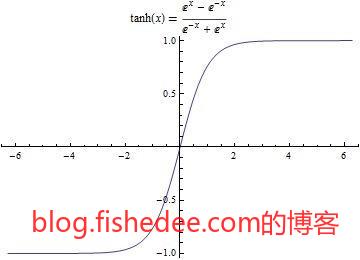
3.2 sigmoid激活函数
tanh就是将输出映射到[-1,1]的范围里
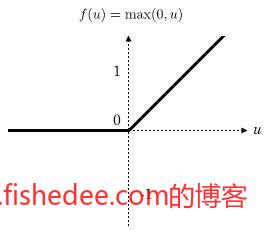
3.3 relu激活函数
relu可谓是打开了新世界的大门，2012年AlexNet碾压ImageNet时就是使用了relu作为激活函数，它的优点是梯度易于计算（不是1，就是0，只有两种），而且梯度不会像sigmoid一样在边缘处梯度接近为0（梯度消失）。
4 异或模拟(XOR)
4.1 模型
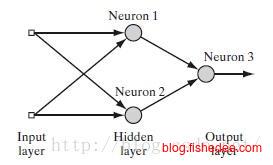
线性回归和逻辑回归我们可以看成是单个神经元的神经网络，现在我们来尝试让神经网络学习异或的逻辑，也就是输入(0，1)和(1,0)时输出1，其他情况时输出0。这个神经网络有一个隐藏层和一个输出层，一共有三个神经元，每个神经元都是带有sigmoid的激活函数。
\[ m_1 = w_1^Tx+b_1\\ n_1 = sigmoid(m_1)\\ m_2 = w_2^Tx+b_2\\ n_2 = sigmoid(m_2)\\ m_3 = w_3^T(n_1,n_2)+b_3\\ n_3 = sigmoid(m_3)\\ y = n_3 \]
\[ loss = \sum_{i=1}^{n}(y_i-\hat{y}_i)^2 \]
它的数学为上面的方程，跟以前的方法一样，我们需要求的各个w和b的梯度就可以了，注意变量很多，你需要留心推导的细节。
\[ \frac {\partial loss}{\partial w_{31}}=\frac {\partial loss} {\partial y}\frac {\partial y}{\partial m_3}\frac {\partial m_3} {\partial w_{31}}\\ = 2\sum_{i=1}^{n}(y_i-\hat{y}_i)\frac {e^{-m_3}} {(1+e^{-m_3})^2}n_1\\ \frac {\partial loss}{\partial w_{32}}=\frac {\partial loss} {\partial y}\frac {\partial y}{\partial m_3}\frac {\partial m_3} {\partial w_{32}}\\ = 2\sum_{i=1}^{n}(y_i-\hat{y}_i)\frac {e^{-m_3}} {(1+e^{-m_3})^2}n_2\\ \frac {\partial loss}{\partial b_3}=\frac {\partial loss} {\partial y}\frac {\partial y}{\partial m_3}\frac {\partial m_3} {\partial b_3}\\ = 2\sum_{i=1}^{n}(y_i-\hat{y}_i)\frac {e^{-m_3}} {(1+e^{-m_3})^2}\\ \]
输出层的梯度就是这样，跟逻辑回归的梯度计算是一样的。
\[ \frac {\partial loss}{\partial w_{11}}=\frac {\partial loss} {\partial y}\frac {\partial y}{\partial m_3}\frac {\partial m_3} {\partial n_1}\frac{\partial n_1}{\partial m_1}\frac{\partial m_1} {\partial w_{11}}\\ = 2\sum_{i=1}^{n}(y_i-\hat{y}_i)\frac {e^{-m_3}} {(1+e^{-m_3})^2}w_{31}\frac {e^{-m_1}} {(1+e^{-m_1})^2}x_{1}\\ \frac {\partial loss}{\partial w_{12}}=\frac {\partial loss} {\partial y}\frac {\partial y}{\partial m_3}\frac {\partial m_3} {\partial n_1}\frac{\partial n_1}{\partial m_1}\frac{\partial m_1} {\partial w_{12}}\\ = 2\sum_{i=1}^{n}(y_i-\hat{y}_i)\frac {e^{-m_3}} {(1+e^{-m_3})^2}w_{31}\frac {e^{-m_1}} {(1+e^{-m_1})^2}x_{2}\\ \frac {\partial loss}{\partial b_1}=\frac {\partial loss} {\partial y}\frac {\partial y}{\partial m_3}\frac {\partial m_3} {\partial n_1}\frac{\partial n_1}{\partial m_1}\frac{\partial m_1} {\partial b_1}\\ = 2\sum_{i=1}^{n}(y_i-\hat{y}_i)\frac {e^{-m_3}} {(1+e^{-m_3})^2}w_{31}\frac {e^{-m_1}} {(1+e^{-m_1})^2}\\ \]
隐藏层的神经单元1的梯度就是这样，神经单元2的计算与此类似，就不再写了。请务必留意这里的计算，这里是bp算法的关键。xor的实现在这里，有两个版本，分别是普通版和向量版
xor的实现中给予了我们启示，无论多深的神经网络，我们都能在理论上用梯度下降的方法来优化它，使得构建一个网络能拟合输入和输出之间的关系。预测时我们用前向计算的方法获得输出，训练时我们从最后一层的loss开始反向计算逐步获得并更新每一层的梯度，这个就是反向传播算法，也就是bp算法。
在反向传播算法中，它的步骤为：
- 先根据loss函数计算输出层的loss，即\(2(y_i-\hat{y}_i)\)
- 计算输出层的grade，方法为输出层的loss乘以激活函数梯度，再乘以输入数值，即\((y_i-\hat{y}_i)\frac {e^{-m_3}} {(1+e^{-m_3})^2}n_1\)
- 计算隐藏层的loss，方法为输出层的loss乘以激活函数梯度，再乘以输出层的权值，即\((y_i-\hat{y}_i)\frac {e^{-m_3}} {(1+e^{-m_3})^2}w_{31}\)
- 计算隐藏层的梯度，方法为隐藏层的loss乘以激活函数梯度，再乘以输入数值，即$\((y_i-\hat{y}_i)\frac {e^{-m_3}} {(1+e^{-m_3})^2}w_{31}\frac {e^{-m_1}} {(1+e^{-m_1})^2}x_{1}\)
从步骤我们可以看出，我们每一步的计算都是，算当前梯度，然后算上一层的loss，不断重复传递的过程。
要注意的是，如果一个隐藏层的数据不只输出到一个输出单元，而是多个输出单元时。这个隐藏层神经元的loss为多个输出神经元的后向loss之和。
4.2 mse损失函数
\[ loss = \sum_{i=1}^{n}(y_i-\hat{y}_i)^2\\ \frac {\partial loss} {\partial y}=2\sum_{i=1}^{n}(y_i-\hat{y}_i) \]
这个可谓是最简单的loss函数，万能但不太准确。
4.3 binary_crossentropy损失函数
\[ loss = -\sum_{i=1}^{n}\hat{y_i}logy_i+(1-\hat{y_i})log(1-y_i)\\ \frac {\partial loss} {\partial y} = -\sum_{i=1}^{n}\frac {\hat{y_i}} {y_i}-\frac {1-\hat{y_i}} {1-y_i} \]
这个是针对概率之间的损失函数，你会发现只有\(y_i\)和\(\hat{y_i}\)是相等时，loss才为0，否则loss就是为一个正数。而且，概率相差越大，loss就越大。这个神奇的度量概率距离的方式称为交叉熵。
4.4 softmax激活函数
softmax激活函数，就是将输入数据取指数，然后归一化后，谁的数值较大谁的概率就越大。这解决了输出数据中概率和必需为1。而且输出概率值与输入值之间成正相关的问题。
\[ \frac {\partial S_i} {\partial V_i}=S_i(1-S_i)\\ \frac {\partial S_i} {\partial V_j}=-S_iS_j \]
softmax的导数也比较麻烦
4.5 categorical_crossentropy损失函数
\[ loss = -\sum_{i=1}^{n}\hat{y_{i1}}logy_{i1}+\hat{y_{i2}}log(y_{i2})+... ++\hat{y_{im}}log(y_{im})\\ \frac {\partial loss} {\partial y_{i1}}=-\sum_{i=1}^{n}\frac {\hat{y_{i1}}} {y_{i1}}\\ \frac {\partial loss} {\partial y_{i2}}=-\sum_{i=1}^{n}\frac {\hat{y_{i2}}} {y_{i2}}\\ ...\\ \frac {\partial loss} {\partial y_{im}}=-\sum_{i=1}^{n}\frac {\hat{y_{im}}} {y_{im}}\\ \]
n是样本数量，m是分类数目，注意，这是一个多输出的loss的函数，所以它的loss计算也是多个的。
一般来说，当最后一层接上softmax作为分类概率输出时，都会用categorical_crossentropy作为损失函数，所以框架中会进行优化，对这两条公式的梯度合起来计算，发现合起来以后，loss计算就会超简单。具体看这里，我就懒得推导了。
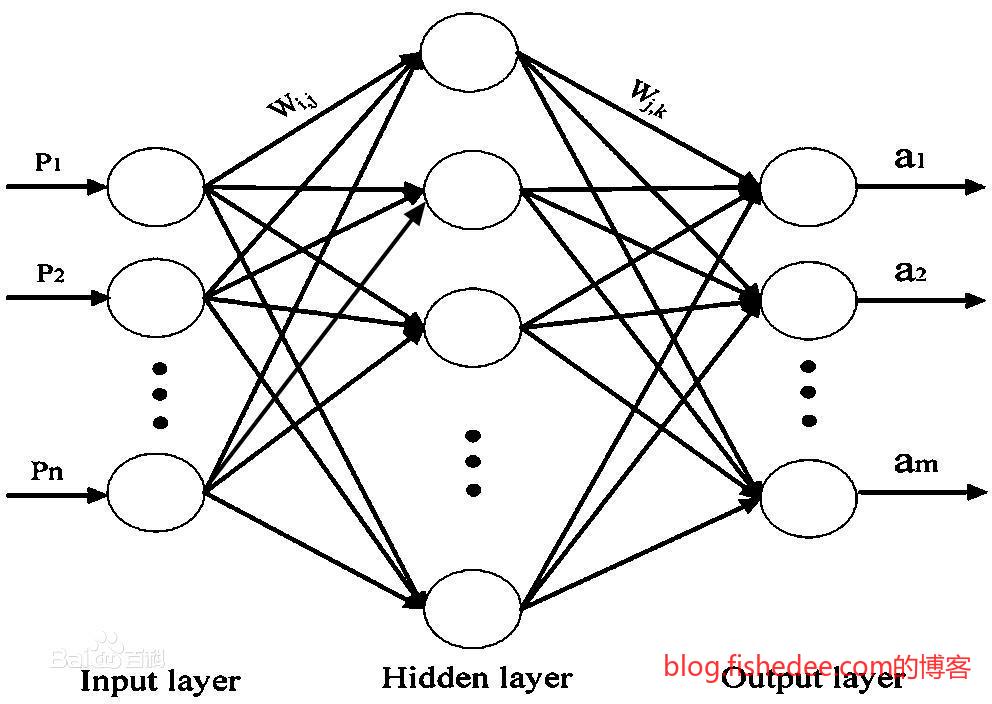
5 多层感知器(MLP)
5.1 框架
model = Model()
model.add(Dense(2,input_shape=(1,2)))
model.add(Activation("sigmoid"))
model.add(Dense(1))
model.add(Activation("sigmoid"))
optimizer = Optimizer(rate=0.1,momentum=0.9)
loss = Loss("mse")
model.compile(optimizer=optimizer,loss=loss)
model.fit(x_train,y_train,epochs=10000)我们要做的深度学习框架上，接口借鉴keras的顺序模型，新建一个模型，然后一层一层到底，接着就是输入优化器和loss，就可以进行训练了。使用代码在这里
def _trainSingle(self,x,y,grade):
if x.ndim == 1:
x = x[:,None].T
if y is not None and y.ndim == 1:
y = y[:,None].T
output = [0]*len(self._layer)
loss = [0]*len(self._layer)
# 前向传播
for i in range(0,len(self._layer)):
weight = self._weight[i]
layer = self._layer[i]
if i == 0:
inData = x
else:
inData = output[i-1]
output[i] = layer.get_output(weight,inData)
# 计算结果
predictY,layerLoss,totalLoss,totalAcc = self._losser.get(output[-1],y)
# 后向传播loss和grade
for i in range(len(self._layer)-1,-1,-1):
weight = self._weight[i]
layer = self._layer[i]
curOutput = output[i]
if i == 0:
preOutput = x
else:
preOutput = output[i-1]
if i == len(self._layer)-1:
nextLoss = layerLoss
else:
nextLoss = loss[i+1]
loss[i] = layer.get_loss(nextLoss,weight,preOutput,curOutput)
grade[i] = grade[i] + layer.get_grade(nextLoss,weight,preOutput,curOutput)
return totalLoss,totalAcc,predictY
def _train(self,x,y):
grade = []
for layer in self._layer:
grade.append(layer.get_init_grade())
# 训练数据
totalLoss = 0
totalAcc = 0
for i in range(0,len(x)):
loss,acc,predictY = self._trainSingle(x[i],y[i],grade)
totalLoss += loss
totalAcc += acc
# 更新梯度
for i in range(0,len(grade)):
grade[i] = grade[i]/len(x)
self._weight = self._optimizer.update(self._weight,grade)
return totalLoss,totalAcc框架的主逻辑就是上面的_train函数，先将数据倒进去获取梯度之和，然后用优化器来更新weight。在_trainSingle函数中，则沿用bp算法，先前向逐层调用get_output，然后通过损失函数计算最后一层的loss，最后是反向逐层调用get_loss和get_grade来获取每一层的梯度信息。
注意，在这里的实现中，每一层的关键在于实现get_output,get_loss和get_grade这三个函数，我把这个函数设计为无状态的，也就是具体层里面不保存output和weight的状态信息，而交由框架来处理，这样更加灵活一点。在现代的深度学习框架(keras,tensorflow等等)中，在你需要编写自定义层时，只需要写类似get_output的函数就可以了，至于grade和loss，框架会自动根据get_output的实现自动推导出来，而且有需要的时候它还能将你写在get_output的python代码转换为gpu的代码让其跑在gpu上从而大幅提高效率，实在牛逼，这就是符号式编程所带来的好处。
框架的主体实现在这里
5.2 全连接层
全连接层，代码在这里，有了xor的铺垫，看到这里就是顺手推舟的事情了，我这里唯一的优化是将多神经元的计算合并为一个矩阵乘法而已。
5.2 激活层
激活层，代码在这里，我把激活层看成是单独的一层神经网络，这里带来了更多的灵活性，也让网络层变得简单点。keras则支持在普通层上指定激活函数的方法。
5.3 正则层
正则层，避免过拟合的一种方法，我在这里只实现了dropout的方法，代码在这里，这可能是实现最简单的一个层了。
值得注意的是，这个简单的正则层可是2012年AlexNet横扫ImageNet的大招之一。
6 卷积神经网络(CNN)
6.1 卷积层
卷积层的实现在《深度学习概览》中已经讲述很清楚了，值得注意的是它的loss和grade的计算，相当有趣。这里有非常棒的推导过程，你会惊讶地发现loss和grade的计算也可以被转化为一个卷积操作。
在没有发现这个方法前，我是将矩阵分解后再卷积，loss计算时是先卷积再合并的，想想都觉得蛋疼。卷积层的代码在这里
6.2 池化层
池化层的方法比较简单，就是卷积核中取最大值那个就可以了，步长就是卷积核的宽度。loss的计算就更简单，取哪个数据loss就回到哪里去，其他地方都是0就可以了。那grade呢？呃，weight都没有，哪里来的grade。
池化层的代码在这里，我没有找到numpy的池化操作，只能手写循环了，没办法了。在反向算loss时我使用了一种同时设置数组多个位置数值的方法，有点贱贱的。
6.3 扁平层
扁平层就是将矩阵压扁到一维而已，毕竟全连接层只支持一维度的输入呀。output和loss的计算都简单得发指。代码在这里
7 mnist实现
有了以上的CNN和MLP的框架后，我们可以随意开工玩弄mnist了。注意，以下的代码中我都偷懒用keras.datasets库来拉取mnist数据集，但是实现框架都是用我自己写的代码，并没有使用keras框架。
另外，所有测试都只跑了2个epoch（大概是95%的准确率），而keras的官方sample在同样模型下，都是跑20个epoch的（大概是98.5%的准确率），千万不要耍流氓地抛开训练次数谈准确率。
7.1 mlp
model = Model()
model.add(Dense(512,input_shape=(1,784)))
model.add(Activation("relu"))
model.add(Dense(512))
model.add(Activation("relu"))
model.add(Dense(10))
optimizer = Optimizer(rate=0.01,momentum=0.9)
loss = Loss("softmax_categorical_crossentropy")
model.compile(optimizer=optimizer,loss=loss)首先上阵的是mlp，两层的全连接层，都是relu的激活函数，loss为softmax+categorical_crossentropy（合并式计算，这样比较快，也能避免指数的溢出问题）。代码在这里
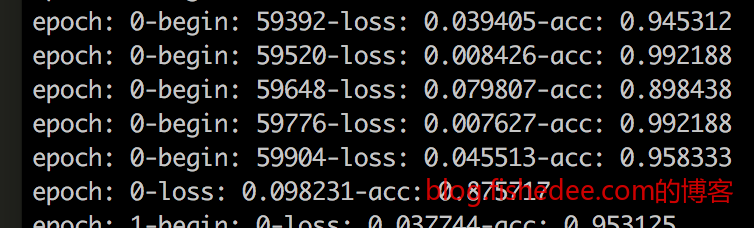
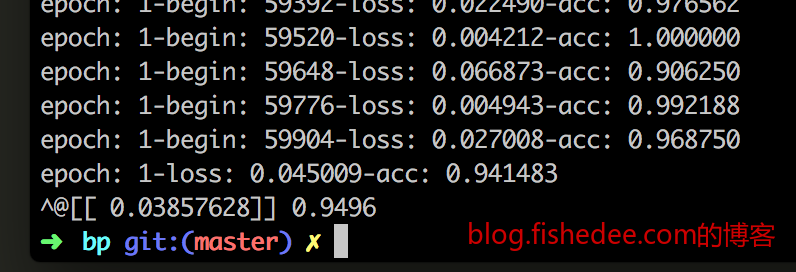
我只跑了训练集两个epoch，花了大概半小时，第一个epoch准确率就已经高达87.6%，第二个epoch准确率就高达94.1%，测试集的准确率是94.9%。
7.2 mlp+dropout
model = Model()
model.add(Dense(512,input_shape=(1,784)))
model.add(Activation("relu"))
model.add(Dropout(0.25))
model.add(Dense(512))
model.add(Activation("relu"))
model.add(Dropout(0.25))
model.add(Dense(10))
optimizer = Optimizer(rate=0.01,momentum=0.9)
loss = Loss("softmax_categorical_crossentropy")
model.compile(optimizer=optimizer,loss=loss)跟mlp差不多，只是加入了两个dropout层，可没有想到，跑得这么慢，快一个小时了，哭。代码在这里
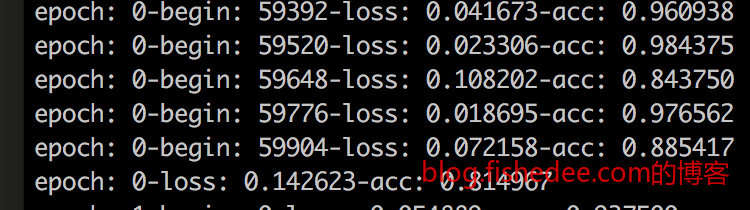
依然只跑了训练集两个epoch，第一个epoch准确率是81.5%，第二个epoch准确率就高达91.5%，测试集的准确率是93.0%。准确率没有单纯MLP的高，也许是因为epoch跑得不够多吧，毕竟dropout带来的随机性这么高，收敛没有这么快的。
7.3 cnn
model = Model()
model.add(Conv2D(32,kernal_size=(3,3),input_shape=(1,28,28)))
model.add(Activation("relu"))
model.add(Conv2D(64,kernal_size=(3,3)))
model.add(Activation("relu"))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(128))
model.add(Activation("relu"))
model.add(Dense(num_classes))
optimizer = Optimizer(rate=0.01,momentum=0.9)
loss = Loss("softmax_categorical_crossentropy")
model.compile(optimizer=optimizer,loss=loss)两个卷积层，一个全连接层，参数量其实比MLP要少，但是计算量却大很多，所以cnn跑两个epoch都超级慢，大概是6个小时，崩溃大哭。代码在这里
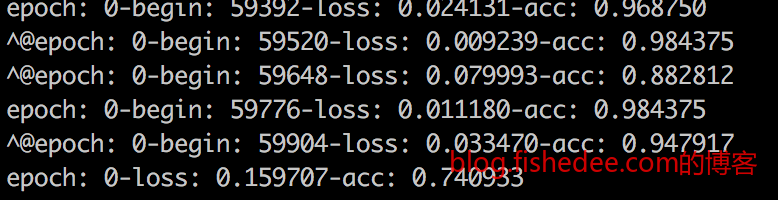
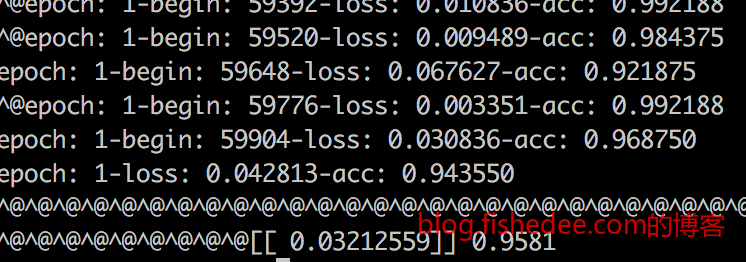
依然只跑了训练集两个epoch，第一个epoch准确率只有74.0%，但第二个epoch准确率就高达94.3%，测试集的准确率是95.8%。收敛速度明显比mlp慢，但进步神速，测试集的准确率是所有测试中最高的，cnn的确是提取图像特征的神器。
8 总结
从开始的入坑神经网络，到网上各种bp算法的推导，我都是看懵的，因为他们的推导大多都是按矩阵的写法来写的，实在看不太懂。然后我用点土办法，一步一步来用单个变量来推导，然后再进一步理解矩阵的办法，就通了。=，=，这也许就是笨人的办法吧。
做完了这个实验以后，大概就能理解整条深度学习的脉络。深度学习从沉寂到兴起的这段时间，实在很有意思，神经网络是1969年提出的，BP算法是1974年提出的，CNN模型是1998年提出的，RNN模型是2004年提出的。但是，这些伟大的想法基本上提出了也没有什么轰动，并没有引起现在的深度学习浪潮，那个时候全是统计学习的天下。
直到2006年Hinton提出了用RBM和DBN来预训练网络来解决深层网络的问题，深度学习在开始重新重视起来。然而，令人惊讶的是，RBM和DBN在当前深度学习的浪潮中作用不大，还不如考虑如何初始化深度神经网络的权重更为重要（这是事实，你发现2017年的深度学习相关论文中已经很少RBM和DBN的踪迹了，大部分的都是CNN和RNN的变种模型）。人们到目前为止，依然是继续发展1998年的CNN和2004年的RNN的变种模型，以及1974年的BP算法来训练深度学习。造成这一变化的更大原因是，GPU的发展，算力的提高，就会发现原来不能收敛的问题都能收敛，原来看起来没有结果的模型训练足够久了竟然也能凑合着用了。也就是说，神经网络的这个模型一直都没有问题，问题是机器的算力在之前一直跟不上而已。呃，这个原因就有点搞笑了，哈哈哈。
虽然，深度学习目前火得不行不行的，但我认为梯度下降的方法始终不是人工智能的尽头，感觉有点奇怪。就像是，我们认识猫和狗的区别时，我们只需要看二三十只就懂了，但是深度学习需要二三百只才能很好地避免过拟合。
并且，更重要的区别在于，即使没有人告诉我们这是猫，那是狗，我们看了二三十只这两种动物后，我们也会知道，这两种东西就是不一样的，他们是可以归为两类的。直到有一天，有人告诉我这个是猫，那个是狗以后，我就能触类旁通，知道这一大类的都是猫，那一大类的都是狗。但是，深度学习仍然需要提前告诉它这是猫，那是狗，它才会抽取恰当的特征出来。它不懂得自己找出相似点，将他们分为两类，更不会触类旁通。换句话说，人类的学习是小样本的无监督学习，但深度学习是超大样本的有监督学习。
所以说，Hiton才会认为梯度下降不是AI的尽头，在他眼里，目前的深度学习还是弱鸡一个，目前，他提出了一项Capsule的模型来接近这个想法。另外，让人更加苦恼的是，为什么这么简单的梯度下降算法和神经网络模型会如此有效，数学家们没有给出一个合理的解释。我们训练出了一个深度学习模型，但我们真的不知道它内部是怎么工作的（这有点像傅立叶变换刚出来的时候，工程师觉得好用，但数学家们也不知道为什么）。我们真的不知道cnn抽取出来的是什么特征，是颜色，是形状，还是方向。如果要新增一种识别模式，我们只能新增标注数据重新训练，不能直接修改神经网络的权值来适应。所以有人说，在这种情况下发展深度学习，就像是一种炼丹的过程。。。。所以我认为现在AI的发展现在还只是很初期的阶段，也许还要再过多2～3个世纪（基础理论的发展还远远没有你想象的这么快，1969年的登月成功后，我们到现在都没有到火星呢）。
当然，总的来说，这一波浪潮已经足够让我们震惊了，2012年的AlexNet横扫ImageNet，2016年的AlphaGo横扫围棋界，我们身边多了很多车牌识别，人脸识别，银行卡号拍照识别，语音识别等的AI例子，深度学习正在改变着我们的生活。
最后，我对深度学习的理解是，奇点远远没有来临，担忧人工智能威胁人类的说法真的是放屁，不信，你看看，那个8000亿美元市值的苹果做出来的siri为啥还是这么弱鸡，前言不搭后语，一看就知道是机器人，根本就过不了图灵测试。
噢，对了，还有一个忠告。不要相信任何用深度学习，AI模型或者大数据模型来炒股票的东西。深度学习的这个模型很明显就是过度依赖监督数据的有效性，高噪音数据直接扔进去训练会过拟合成什么鸟样呀，分分钟被对手利用了都不知道为什么。
- 本文作者： fishedee
- 版权声明： 本博客所有文章均采用 CC BY-NC-SA 3.0 CN 许可协议，转载必须注明出处！