1 概述
数据结构概览
2 哈希
2.1 余数桶
2.1.1 结构
\[ hash[data] = data \mod n \]
余数桶的想法很简单,将数据取余数得到哈希值,然后存放到对应的桶中。
2.1.2 用途
余数桶用法最为直接,可以用来作为数据的精确查找
2.2 基数桶
2.2.1 结构
\[ hash[data] = data / n \]
基数桶取的是data的商,而不是余数,那么在使用时就需要先确定data的取值范围,然后确定n是多少,以保证商的范围都在桶的范围中。例如,data的取值范围为[100000,9999999],data的具有7位数,桶的数量为100,2位数,那么n就要取10000。
2.2.2 用途
基数桶的用途就大得多了,基数桶除了像余数桶一样实现了映射的功能,它还能保留了数字原来的大小关系。所以它不仅可以做精确查找,还可以做范围查找。
\[ count(k)\\ st. i < k < j\\ 相当于\\ count(k)+count(m)+count(n)\\ st. hash[i]<hash[k]<hash[j]\\ st. hash[m] = hash[i] 且 m > i\\ st. hash[n] = hash[j] 且 n > j\\ \]
基数桶的范围查找跟树的范围查找的方式不同的是,它可以是跳跃式的,能在O(1)范围内定位到边界的位置,但是统计数据就比树要慢一点的了
\[ max(data[k])\\ st. k>=i 且 k <= j\\ \]
我们也可以用基数桶来做数据的预处理,例如,假设i是一堆浮点数和对应的data[i]数值,我们要求一个范围中的最大数值data。当i和j是定点数时,我们可以用线段树来解决。在这个问题中,由于i和j都是浮点数,我们不能预先计算出所有的i和j的数值,从而不能直接使用浮点数。
\[ hash[i] = i / n \]
但是我们可以通过一层转换将i转换为ihash,然后在ihash上建立线段树
\[ max(data[k],data[m],data[n])\\ st. hash[k]> hash[i] 且 hash[k] < hash[j]\\ st. hash[m]=hash[i] 且 m >=i\\ st. hash[n]=hash[j] 且 n <= j \]
统计时分三部分来统计,分别是线段树上的开区间统计,然后是左边缘和右边缘位置的朴素统计就可以了。
思考一下,这种使用哈希作为预处理的方法,为什么不能使用余数桶的方法。
2.3 多维余数桶
2.3.1 结构
\[ hash[data].x = data.x \mod n\\ hash[data].y = data.y \mod n\\ \]
如果数据本身是多维的,我们将数据每一维进行哈希,然后也得到一个多维哈希值,这就是多维余数桶。
2.3.2 用途
和余数桶一样,做多维数据的精确查找
2.4 多维基数桶
2.4.1 结构
\[ hash[data].x = data.x / n\\ hash[data].y = data.y / n\\ \]
数据是多维的时候,我们将数据每一维进行哈希,只是使用的是基数哈希,这样保持了原来数据的大小关系。
2.4.2 用途
\[ \sqrt{(a.x-b.x)^2+(a.y-b.y)^2}<=distance \]
多维基数桶的除了可以做精确查找,范围查找外,还可以做欧几里得距离查找。例如,我们在已知到a点的情况下,求满足距离a点的欧几里得距离少于distance的b点。
\[ \lvert a.x-b.x \rvert < distance\\ \lvert a.y-b.y \rvert < distance\\ \]
显然,满足欧几里得距离少于distance的b点的必要条件是,b点的横坐标和纵坐标的直线距离都少于distance。注意是必要条件,不是充分条件。
\[ hash[a].x = a.x / distance\\ hash[a].y = a.y / distance\\ 然后寻找 b\\ st. hash[b].x = hash[a].x或hash[a].x+1或hash[a].x-1\\ st. hash[b].y = hash[a].y或hash[a].y+1或hash[a].y-1\\ \]
我们可以先将点a执行基数桶哈希,然后对所有点也执行基数桶哈希,然后查找a点附近的基数桶就可以了,这时候时间复杂度为\(O(1)\),最后在满足直线距离少于\(2*distance\)的点中寻找欧几里得距离少于distance的b点就可以了。
能够快速计算最近欧几里德距离有什么用?基于geohash的附近点查找,基于hash的最近邻特征向量查找都是来源于这个算法。
3 并查集
3.1 结构
int set[max];
void Make_Set(int i)
{
set[i]=i;//初始化的时候,一个集合的parent都是这个集合自己的标号。没有跟它同类的集合,那么这个集合的源头只能是自己了。
}
int Find_Set(int i)
{
//如果集合i的父亲是自己,说明自己就是源头,返回自己的标号
if(set[i]==i)
return set[i];
int parent = Find_Set(set[i]);
set[i] = parent;
return parent;
}
void Union(int i,int j)
{
i=Find_Set(i);
j=Find_Set(j);
set[i] = j;
}并查集就这么简单,其中Find_Set加入了路径压缩的算法,基本上可以将时间复杂度看作为常数。
3.2 用途
- 可以任意合并两个元素所在的集合
- 查询两个元素是否在同一个集合
并查集就是用来做集合的两个操作,一般用来做图类题目的查询优化。
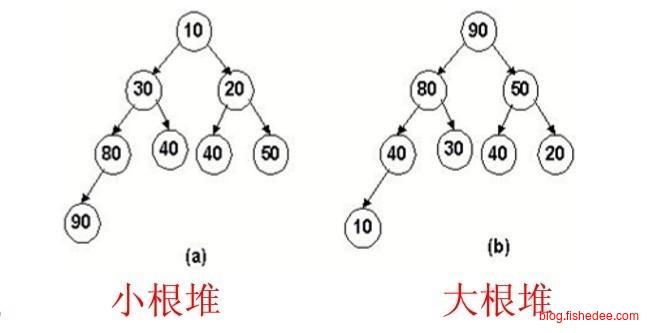
4 堆
4.1 堆
4.1.1 结构
\[ 最小堆:heap[x] < heap[x.left] 且 heap[x] < heap[x.right]\\ 最大堆:heap[x] > heap[x.left] 且 heap[x] > heap[x.right]\\ \]
最小堆和最大堆的定义就是以上的两条公式,相当简单,那么在查找最值时就相当简单,就是根部的数值了。
void heapUpIfy(int[] heap ,int index){
int data = heap[index];
while( index > 1 ){
int parent = index/2;
if( heap[parent] < data){
heap[index] = heap[parent];
index = parent;
}else{
break;
}
}
heap[index] = data;
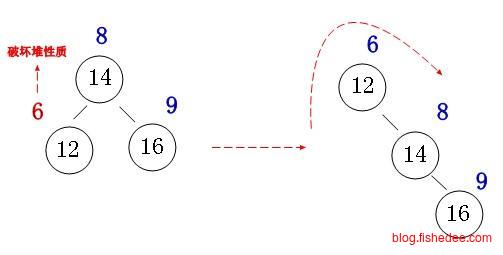
}最大堆的维护有两种方式,一种是尾部添加数据时,在尾部的位置开始往顶部开始调整,以保持最大堆的性质。
void heapDownIfy(int[] heap,int size,int index){
int data = heap[index];
while( index*2 < size ){
int leftChild = index*2;
int rightChild = index*2+1;
int maxChild = -1;
if( heap[leftChild] > heap[rightChild]){
maxChild = leftChild;
}else{
maxChild = rightChild;
}
if( data < heap[maxChild] ){
heap[index] = heap[maxChild];
index = maxChild;
}else{
break;
}
}
heap[index] = data;
}另外一种就是根部删除数据,然后将最后一个元素替换到根部以后,从根部开始往下调整,以保持最大堆的性质。
4.1.2 用途
\[ max(data[i])\\ st. 0 < i 且 i < n \]
void addData(int data);
int getMax();
void setMax(int data);
void delMax();堆的最直接使用就是维护一个最大值列表,其支持添加数据,然后对最值数据的获取,设置,删除的操作。这个数据结构被用作堆排序,以及外部排序中的多路归并。
\[ data[k]\\ st. data[i]<data[k] 且 count(i) = n/2\\ st. data[j]>data[k] 且 count(j) = n/2\\ \]
void addData(int data);
int getMaxK();
void setMaxK(int data);
void delMaxK();堆的另外一个用法用在维护具体的某个第k大的数据上。
void addData(int data){
if( data < getMaxK() ){
oldMax = 最大堆.getMax()
最大堆.delMax()
最小堆.addData(oldMax)
最大堆.addData(data)
}else{
最小堆.addData(data)
}
}
int getMaxK(){
return 最大堆的根部数据
}
void setMaxK(int data){
delMaxK();
addData(data);
}
void delMaxK(){
min = 最小堆.getMin();
最小堆.delMin();
最大堆.delMax();
最大堆.addData(min);
}方法为维护两个堆,一个最大堆的大小固定为k个,一个最小堆的大小固定为n-k个,而且最大堆的数据都少于最小堆的数据。然后,让每个操作都保证维持这个性质就可以了。
4.2 赢者树
4.2.1 结构
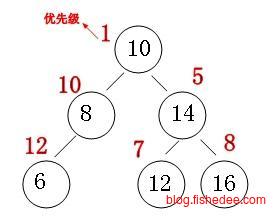
堆在setMax操作后,会执行heapDownIfy往下调整,每次调整时都需要对其的左右两个孩子比较一次。这样的话,每一层的调整都需要两次比较操作。赢者树的出发点是让调整时每一层的操作只需要一次的比较操作。
\[ 最大赢者树:tree[x]\\ st. data[tree[x]]=max(data[tree[x.left]],data[tree[x.right]])\\ st. tree[x] = tree[x.left] 或 tree[x] =tree[x.right]\\ 最小赢者树:tree[x]\\ st. data[tree[x]]=min(data[tree[x.left]],data[tree[x.right]])\\ st. tree[x] = tree[x.left] 或 tree[x] =tree[x.right]\\ \]
它的改进为,树的叶子结点放所有的原始数据,内部结点放原始数据的聚合数据,不像堆一样在内部结点放原始数据。要注意的是,叶子结点和内部结点放的都是数组的下标,而不是数组的值。
void treeUpIfy(int[] array, int[] tree, int[] index){
int treeIndex = n + index;
while( treeIndex > 1 ){
int parent = treeIndex /2;
int leftChild = parent*2;
int rightChild = parent*2 +1;
int maxChild;
if( array[tree[leftChild]] > array[tree[rightChild]] ){
maxChild = leftChild;
}else{
maxChild = rightChild;
}
if( tree[parent] == tree[maxChild] &&
tree[maxChild] != index){
break;
}
tree[parent] = tree[maxChild];
treeIndex = parent;
}
}然后在维护赢者树性质时,只需要和它的另外一个孩子作比较就可以了,所以每一层的维护只需一次的比较操作,大幅减少到为堆的一半比较次数,当然,代价是赢者树的树高会比堆高一层。总体来说,很值得,速度更快。
4.2.2 用途
void addData(int data);
int getMax();
void setMax(int data);
void delMax();对于堆里面的操作,赢者树都可以做。
void setData(int index,int data);另外,由于赢者树的原始数据都是在叶子结点,我们甚至能随意改变数组的任一位置数据,然后再获取最大值。
int getMaxRange(int left, int right)而且,我们能得到任意区间内的最值,因为各个内部结点都缓存了这个区间的最值。任意区间的最值就是将各个子树的最值合并起来就可以了。
4.3 败者树
4.3.1 结构
赢者树在treeUpIfy操作时,需要得到parent结点,然后得到左右两个子结点,最后再作出比较。也就是说这个过程,需要两次对tree数组的访存才能实现。败者树的出发点是,能不能在每一层比较时,对tree数组只需要一次的访存就可以了。
\[ 最大败者树:tree[x]\\ st. data[tree[x]]=min(data[tree[x.left]],data[tree[x.right]])\\ st. tree[x] = tree[x.left] 或 tree[x] =tree[x.right]\\ 且\\ data[tree[0]] = max(data[i]),0<i<n\\ 最小败者树:tree[x]\\ st. data[tree[x]]=max(data[tree[x.left]],data[tree[x.right]])\\ st. tree[x] = tree[x.left] 或 tree[x] =tree[x.right]\\ 且\\ data[tree[0]] = min(data[i]),0<i<n\\ \]
它的改进为,内部结点放的是比较过程中失败的那一方,而最根部结点放的又是最终的胜利者。这样做的原因在于,在setMax操作的treeUpIfy中,它的上一层parent结点原来肯定就是自身的,从parent结点中是肯定得不到兄弟结点内容的,所以,我们每一次都必须要访问兄弟结点。但是在败者树中我们故意存放的是失败者,那么在setMax操作的treeUpIfy中,它的上一层parent结点原来肯定就是兄弟结点,那么我们只需要对parent结点作一次访存操作比较就可以了,不再需要再访问兄弟结点了。当然,在treeUpIfy的过程中我们需要将最终胜利者都一路记录到临时变量中,并最终记录在tree[0]中。
4.3.2 用途
void addData(int data);
int getMax();
void setMax(int data);
void delMax();
void setData(int index,int data);对于败者树来说,以上四个操作都能执行。而setMax操作会能比胜者树少一半的访存操作,setData操作则跟胜者树是一样的访存操作。
int getMaxRange(int left, int right)但是对于getMaxRange它无法做到,因为它的内部结点存的是败者,而不是胜者。当然,你可以实现getMinRange,不过这种场景倒是很少见了。
总的来说,败者树相对胜者树来说,重点优化了setMax性能,但丢掉了区间最大值的能力,所以,只用在setMax操作非常频繁的场景,例如是外部排序中的多路归并。
5 平衡树
5.1 结构
5.1.1 BST树(二叉搜索树)
\[ st. tree[x]>tree[i],\forall i \in x.left\\ st. tree[x]<tree[j],\forall j \in x.right\\ \]
BST树就是满足以上两个性质的树,它的左子树的所有元素都少于自身的节点,它的右子树的所有元素都大于自身的节点。注意是都大于或都少于,而不是只是直接的孩子满足这个性质。
void find(tree,data){
if( tree == null ){
return false;
}else if( tree.data == data){
return true;
}else if( tree.data > data){
return find(tree.left,data);
}else{
return find(tree.right,data);
}
}那么,在BST树上搜索就很简单了,相当于二分查找在树上的实现而已。
添加数据时也很简单,在最后一个找到的节点中添加这个数据就可以了。可能在左子树也可能在右子树,具体要看添加的数据和最后一个找到节点的大小比较。
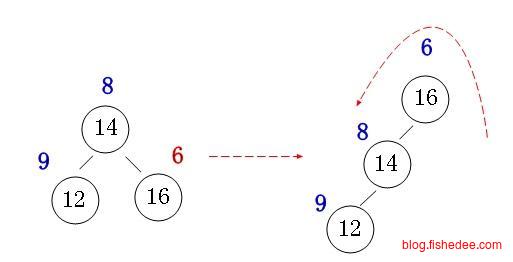
删除数据时麻烦一点,需要分三种情况:
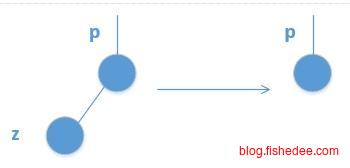
- 要删除的节点z没有孩子节点,那么直接删除节点z就可以了。
- 要删除的节点z只有一个孩子节点,那么删除节点z,并让它的唯一孩子代替节点z的位置就可以了。
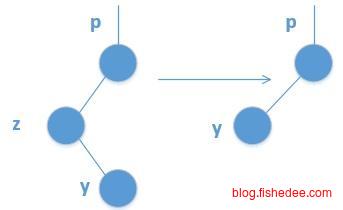
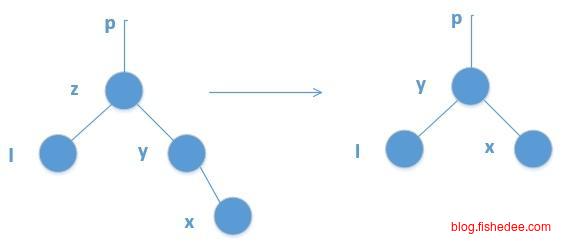
- 要删除的节点z有两个孩子节点,那么有两种方法,一是让节点z的前驱节点y代替节点z,然后删除节点y原来的位置。二是让节点z的后驱节点y代替节点z,然后删除节点y原来的位置。
BST树在随机数据的情况下运行得很好,速度很快,但是在部分最坏的情况下,树的高度会退化到\(O(n)\),导致搜索的速度极慢。
5.1.2 AVL树(高度平衡树)
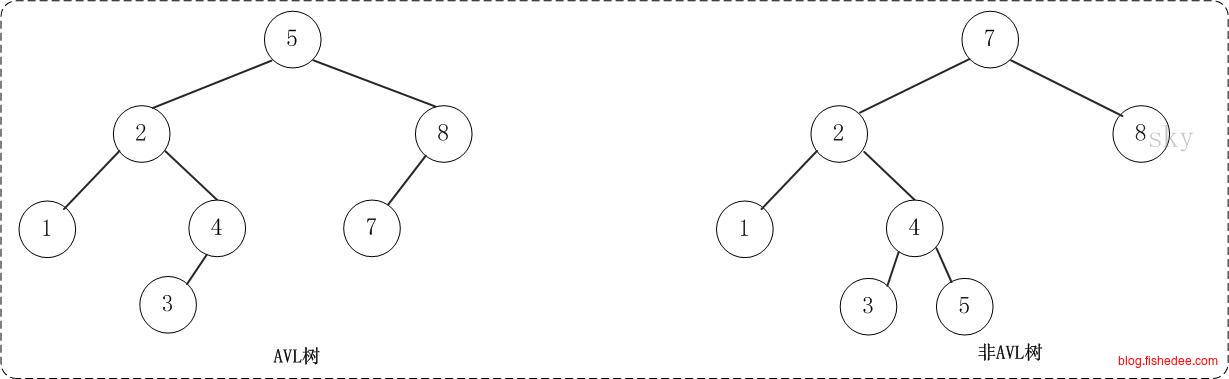
AVL树的想法很简单,就是在每个子树中加入一个数据,高度,根据子树的高度来约束BST树的总高度,使得AVL树的高度最大不会高于\(O(logn)\),避免最坏情况下退化到线性搜索。
\[ st. tree[x.left].height-tree[x.right].height <= 1\\ st. tree[x.right].height-tree[x.left].height <= 1\\ \]
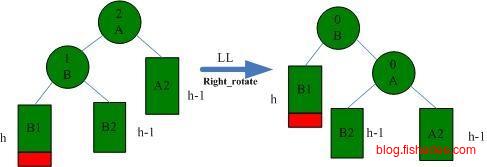
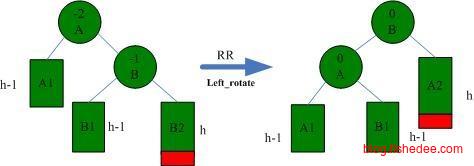
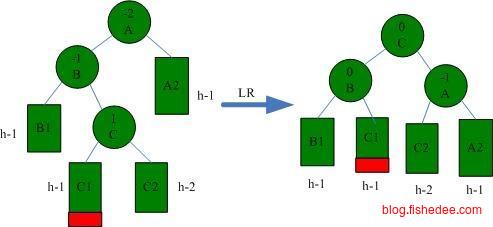
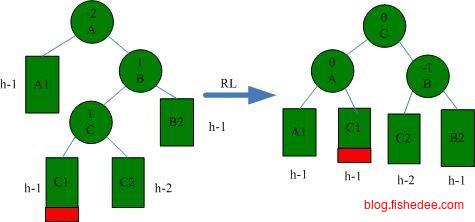
AVL树的约束为,左子树和右子树高度的差值不超过1。所以,当添加或删除数据后,我们需要从叶子结点开始回溯到根结点,看有没有违反AVL树约束的子树,有的话根据以下的四种情况进行调整。
LL情况下的一次右旋转
RR情况下的一次左旋转
LR情况下的一次左旋转,然后右旋转
RL情况下的一次右旋转,然后左旋转
就这么简单,AVL树算是最简单的平衡树结构了。
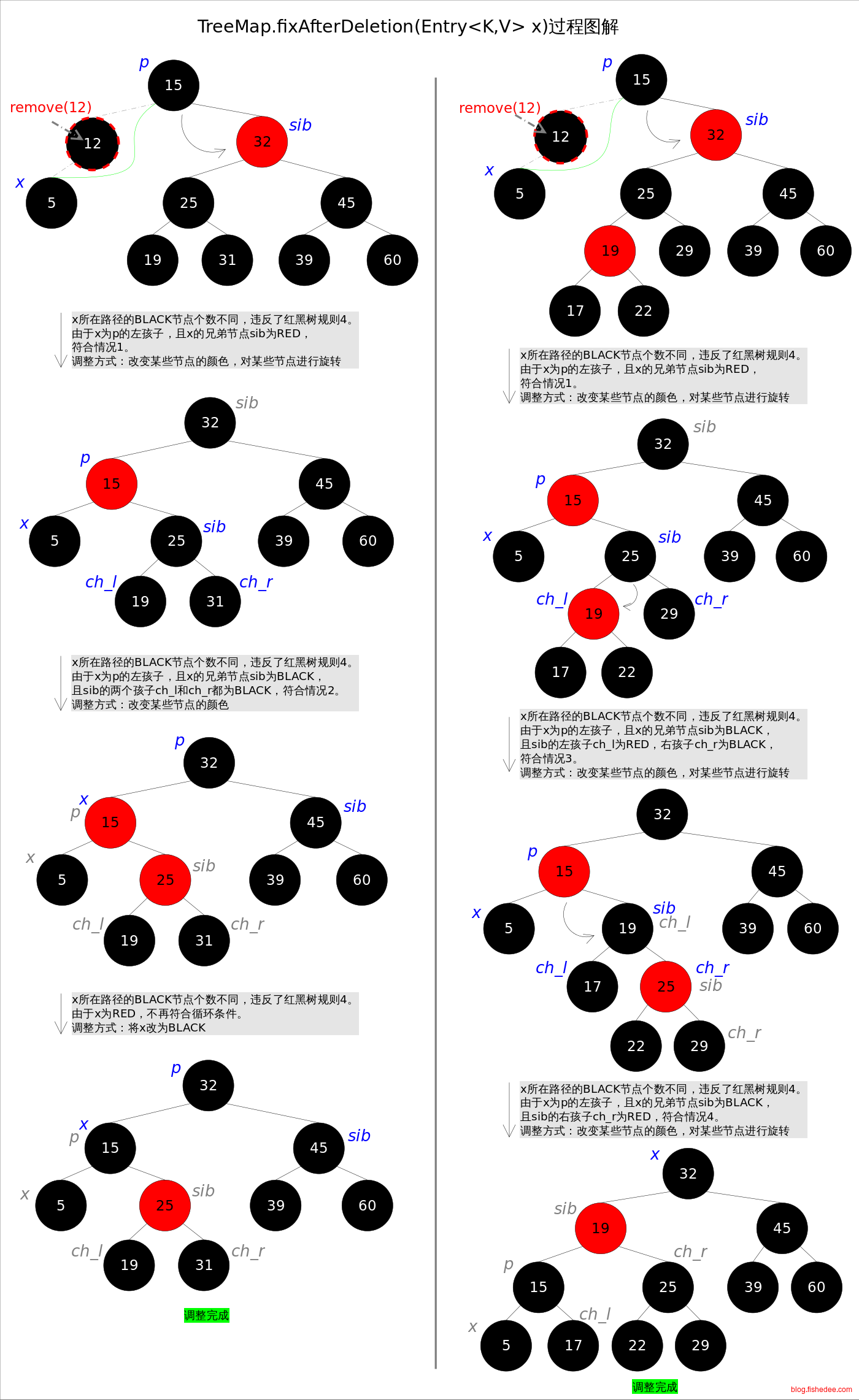
5.1.3 RBT树(红黑树)
1. 每个结点要么是红的,要么是黑的。
2. 根结点是黑的。
3. 每个叶结点,即空结点(NIL)是黑的。
4. 如果一个结点是红的,那么它的俩个儿子都是黑的。
5. 对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。红黑树是另外一种的平衡树,它对BST树的约束为以上5点
1. 根结点和叶子结点都是黑色的
2. 根结点和叶子结点的所有路径都是相同的黑色结点。
3. 一个父子孙关系中,两个相近的黑色结点中只允许最多插入多一个红色结点。5点约束比较难懂,它等价于以上的3点约束,由于两个相近的黑色结点中只允许最多插入多一个红色结点,那么很明显,红黑树的高度最大为\(O(log2n)\)。最坏情况就是所有的两个相近的黑色结点中间都含有一个红色结点,这时候高度大概为AVL树的2倍,但是红黑树的需要调整的情况要少得多,所以常数较小,是目前速度最快的平衡树实现。
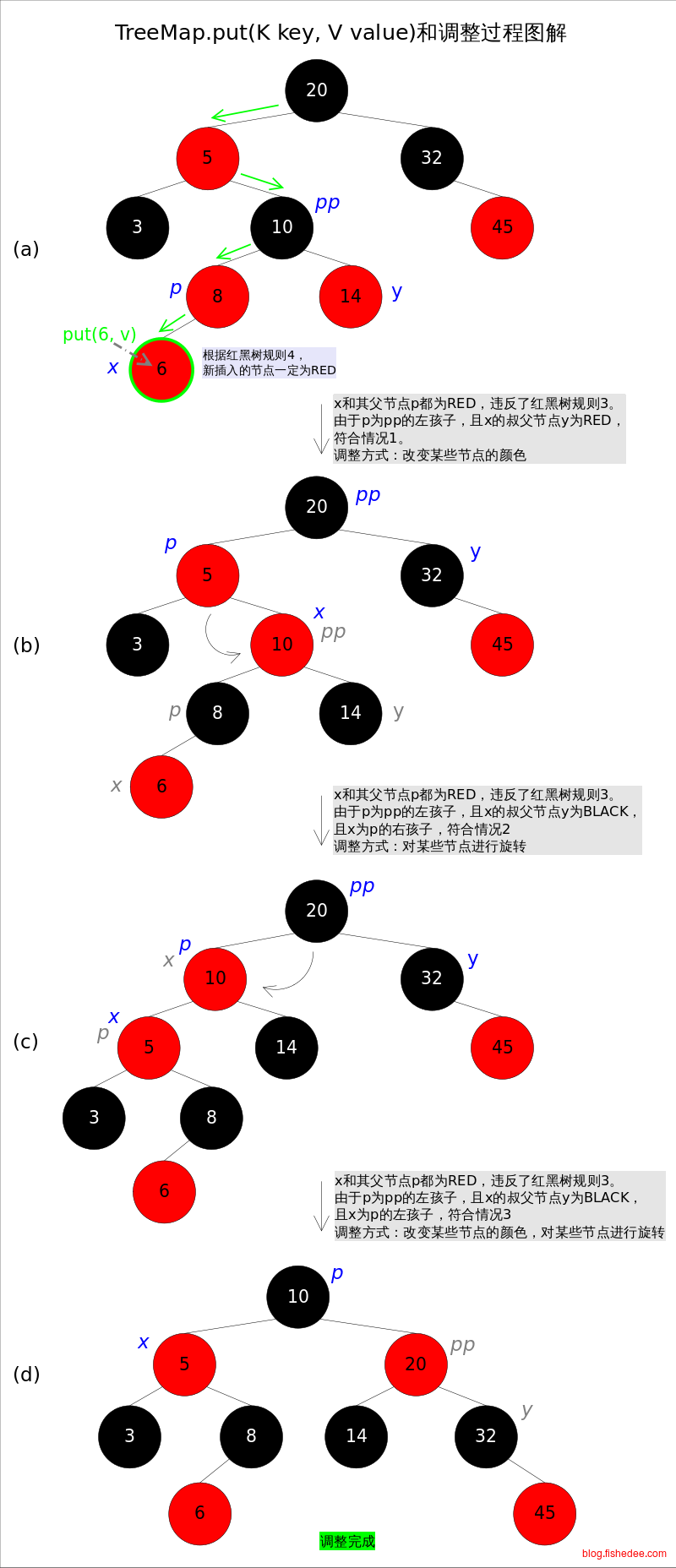
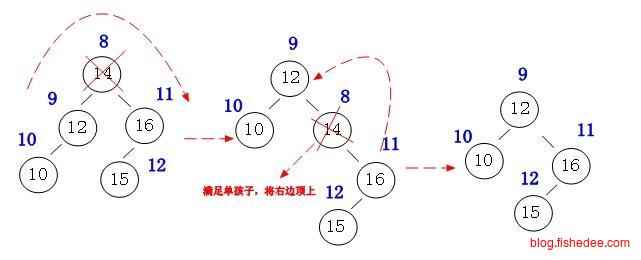
插入时,将新建的节点涂为红色,然后挂在父节点下面,这时候会有以下的四种情况:
- 父节点为黑色。这代表当前的路径有盈余的空间,不需要调整。对应情况d。
- 父节点为红色,且叔父节点也为红色。这代表父节点已经饱满了,而且叔父节点也是饱满的,无法将子节点往叔父节点迁移了,所以将父节点和叔父节点都涂为黑色,然后将祖父节点涂为红色。下一次,将从祖父节点开始调整。对应情况a。
- 父节点为红色,且叔父节点为黑色,且子节点在叔父节点的外侧。这代表,因为父节点为红色,所以子节点的兄弟节点肯定为黑色的,代表着兄弟节点路径是盈余的空间,因此执行一次右旋转将兄弟节点迁移到叔父节点,从而降低父节点的高度,并提高叔父节点的高度。对应情况c。
- 父节点为红色,且叔父节点为黑色,且子节点在叔父节点的内侧。这代表了兄弟节点不能直接移到叔父节点上,但是我们可以通过先执行一次左旋转将本节点高度降一,变为盈余的路径,从而转换到情况c中。下一次,将从原来的父节点开始调整。对应情况b。
总的来说,插入的想法,尽可能将子节点往盈余的叔父节点迁移,如果叔父节点已经饱满了,就将父节点和叔父节点都改为黑色,表示增加一层,然后将这个问题抛给祖父节点。
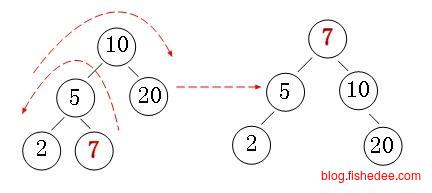
首先,红黑树的删除和BST树删除是一样,最后都是归结于删除一个最多只有一个子节点的节点。所以,红黑树的调整也只需要讨论如何删除一个最多只有一个子节点的结点。然后,删除这个节点时有四种情况。
- 删除节点为红色。这代表本身这条路径就是有盈余的,然后删除了这个盈余的地方也不碍事。所以不调整。
- 删除节点为黑色,它的父节点为黑色,它的兄弟节点为黑色。这代表无法从兄弟节点或父节点来借调节点了,所以将兄弟节点涂为红色。下一次,调整位置从父节点开始。代表将这个问题扔给上一级解决。
- 删除节点为黑色,它的父节点为黑色,它的兄弟节点为红色。这代表兄弟节点是饱满的,这个时候左旋转一下,将兄弟节点拿一个多余的过来。下一次,调整位置依然从本位置开始。对应情况,第一行第一列,和第一行第二列。
- 删除节点为黑色,它的父节点为红色,它的兄弟节点为黑色且其所有子节点都是黑色。这代表兄弟节点是盈余的,那么将父节点和兄弟节点交换一下颜色就可以了。对应情况,第三行第一列。
- 删除节点为黑色,它的父节点为红色,它的兄弟节点为黑色且其左孩子为黑色,右孩子为红色。这代表兄弟节点是左侧饱满的,左旋转一下,将兄弟节点多余的扔过来,然后交换一下和父节点的颜色就可以了。对应情况,第三行第二列。
- 删除节点为黑色,它的父节点为红色,它的兄弟节点为黑色且其左孩子为红色。这代表兄弟节点是左侧盈余的,不能直接左旋转,先右旋转一下,然后转换到上一个情况就可以了。对应情况,第二行第二列。
总的来说,删除的想法是,尽可能将盈余的兄弟节点补过来删除的这一边,如果兄弟节点是饱满的,就尽可能从盈余的父节点补过来,如果父节点都不是盈余的,那么就将父节点所在子树整体高度减一,然后抛给上一层来解决。
5.1.4 SBT树(大小平衡树)
\[ st. tree[x.left].size>tree[x.right.left].size\\ st. tree[x.left].size>tree[x.right.right].size\\ st. tree[x.right].size>tree[x.left.left].size\\ st. tree[x.right].size>tree[x.left.right].size\\ \]
SBT树的想法很简单,就是在每个子树中加入一个数据,节点数量,根据子树的数量来约束SBT树的总高度,使得SBT树的高度最大不会高于\(O(logn)\),避免最坏情况下退化到线性搜索。它的约束为,子树的数量总是大于兄弟子树的数量。
它的调整情况只有四种,非常简单,跟AVL树其实差不多。
\[ tree[x.right].size<tree[x.left.left].size \]
右旋转一次,然后递归调整子树T和子树L
\[ tree[x.right].size<tree[x.left.right].size \]
左旋转一次,然后右旋转一次,然后递归调整子树L和子树T。
其他两种情况和这两种情况,就不啰嗦了。
呃,只能说这个算法相当暴力了,不像AVL树每种情况都是只需要最多旋转两次,然后往上调整。SBT树是每种情况旋转以后,还要往下递归调整,再往上调整,实在坑。所以它的平摊时间复杂度为\(O(logn)\),并没有AVL的快。当然,好处就是多了一个size字段,可以用来做rank的操作。
5.1.5 Treap树
\[ st. tree[x].heap < tree[x.left].heap \\ st. tree[x].heap < tree[x.right].heap \]
Treap树的想法是让二叉树既要满足二叉搜索树的性质,也要满足堆的性质。它加入一个随机的优先级字段,然后在插入和删除时,Treap树必须要按照优先级字段满足堆的性质。在这个例子中,是最小堆的性质。那么优先级字段哪里来,答案是随机给予的,这让我们生成的Treap树是随机的高度,很难会退化到线性的复杂度\(O(n)\)。
插入时相当简单,如果插入数字比父节点还要小,就违反堆的性质,解决办法就是将插入节点旋转到根节点就可以了。
删除时也很简单,将被删除节点往下旋,直到被删除节点没有两个子节点的情况就可以直接删除了。至于往下旋时是左旋还是右旋,那得看左右两个孩子哪个比较小了。当然,你可以用BST的删除方法,只是看起来没有那么优雅了。
Treap树相当有趣,建立了一种heap+tree的数据结构,然后利用随机的优先级来获取期望时间复杂度为\(O(logn)\)的结构。而且编程非常简单,真的很有用。
5.1.6 Splay树
Splay树更加暴力和神奇,它不需要任意的维护字段,每次增加,删除和搜索时就将相应节点旋转到根节点就可以了。
但是,要注意的是,Splay树为了往上旋转到根节点时,不是直接用单左旋转或单右旋转就可以了,因为这样很容易会将树伸展为线性。
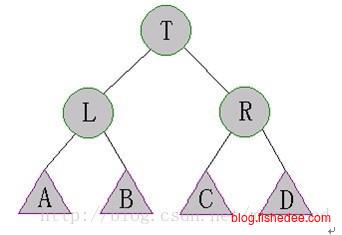
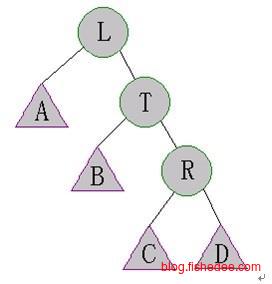
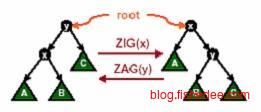
当x节点的父节点y是根节点时,直接用单左旋转或单右旋转。
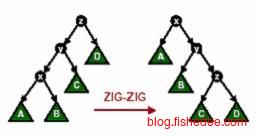
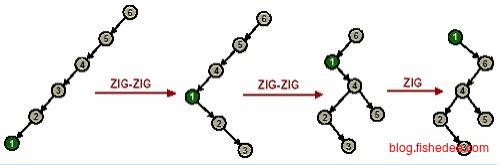
当x节点的父节点y不是根节点时,且都倾向一侧时,从祖父节点z开始两次右旋转,即zig-zig。这种旋转成为一字形旋转。
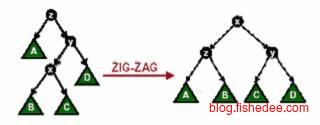
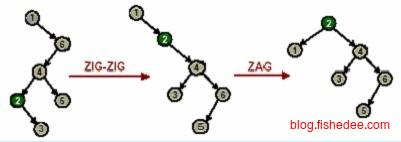
当x节点的父节点y不是根节点时,且不都倾向一侧时,从父节点y开始两次混合旋转,即zig-zag。这种旋转成为之字形旋转。
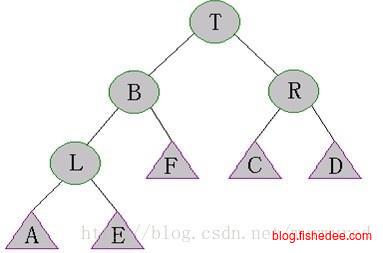
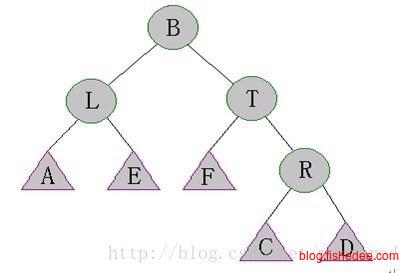
这两个例子说明了使用Splay的伸展方式,注意第一个例子中如果只使用单旋转就会退化到线性链表。
那么,有了伸展操作后,其他就很简单了
- 按照BST插入节点,然后用伸展操作将新插入的节点旋转到根部
- 按照BST删除节点,然后用伸展操作将删除节点的父节点旋转到根部
- 按照BST搜索节点,然后用伸展操作将搜索得到的节点旋转到根部,如果节点不存在,就将最近节点的父节点旋转到根部。
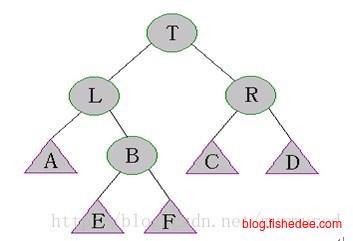
另外,伸展操作的神奇在于,它能很容易实现区间信息维护。例如,我们要查询[a,b]区间的统计信息,可以先将a旋转到根部,然后将b旋转到根部的右子树中。那么(a,b)的信息就是图中的*子树了。而且,相比较线段树而言,Splay树还能支持中间插入和中间删除节点。
5.1.7 替罪羊树
\[ st. tree[x].size*\alpha >= tree[x.left].size\\ st. tree[x].size*\alpha >= tree[x.right].size \]
好了,在见识到SBT树和Treap树的暴力后,我们最后来介绍终极暴力树——替罪羊树。它的约束条件是任意定义的,当约束条件不成立时,它的方法就是将树拍扁,重新建树就可以了,不需要任何的旋转操作。所以被称为终极暴力的平衡树,而且这种思想也被用在了四叉树,k-d树重建上。它的时间复杂度期望为\(O(logn)\),我们定义的约束为,任一子树的数量不大于总树的$\(\alpha\),也就是避免单一子树过于偏斜了。当然,你也就不要将\(\alpha\)设置为0.5,这几乎是每插入一次都要重平衡,大概将\(\alpha\)设置为0.75就可以了。
void Travel(Scapegoat_Tree *p, vector<Scapegoat_Tree *> &v) {//构建一个序列,维护
if(p == NULL)
return;
Travel(p -> l, v);
if(p -> flag == true)
v.push_back(p);
Travel(p -> r, v);
}
Scapegoat_Tree *Divide(vector<Scapegoat_Tree *> &v, int l, int r) {//插入后维护,要不要重构
if(l >= r)
return NULL;
int mid = (l + r) >> 1;
Scapegoat_Tree *p = v[mid];
p -> l = Divide(v, l, mid);
p -> r = Divide(v, mid + 1, r);
p -> PushUp();
return p;
}
void NewBuild(Scapegoat_Tree *&p) {//重构
static vector<Scapegoat_Tree *> v;
v.clear();
Travel(p, v);
p = Divide(v, 0, v.size());
}怎样拍扁重建,首先按照先序遍历将数据放入数组,这时候数组中的数据就是有序的,然后用每次建树都用中位数来建树,达到最优建树效率。
5.2 用途
平衡树大家族是数据结构中最为重要的结构
5.2.1 搜索
Data get(int key);
void set(int key,Data value);
void add(int key,Data value);
void del(int key);
bool exist(int key);最直接的用法就是当成一个搜索的容器,增删改查都没有问题。
[]Data getRange(int key1,int key2);而且,跟哈希搜索不同的是,它支持范围搜索。
5.2.2 数量维护
int getCount();
int getCountInRange(int key1,int key2);在平衡树上加入一个size的字段,我们就能很容易得到一个范围的数据(Splay树)。
int getKeyByRank(int rank);
int getRankByKey(int key);
int getKeyByRankInRange(int rank,int key1,int key2);
int getRankByKeyInRange(int key,int key1,int key2);有了size字段后,我们能进一步排名的信息,根据排名获取key,以及根据key获取排名都没问题,以及范围下的结果(Splay树)
5.2.3 最值维护
Data getMax();
Data getMaxInRange(int key1,int key2);获取整个平衡树的最值,或者是区间的最值都可以(Splay树)
5.2.4 和值维护
Data getSum();
Data getSumInRange(int key1,int key2);跟最值维护是类似的,就不多说了。
5.2.5 众数
int getMode();
int getModeInRange(int key1,int key2);获取在key上的众数,或者是区间上的众树(Splay树),其实就是key上加入一个count字段,然后每次都取count的max的key而已。
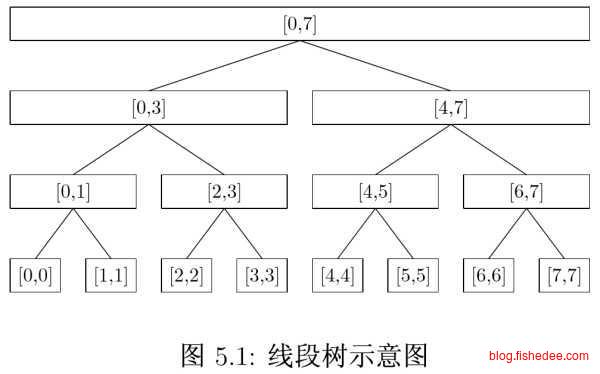
6 线段树
6.1 结构
6.1.1 普通线段树
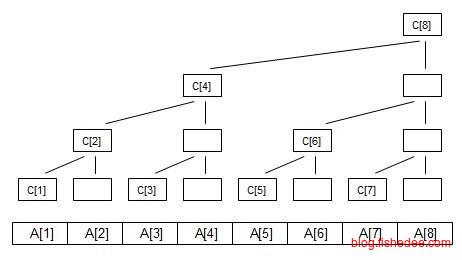
线段树就像我们之间说过的赢者树一样,叶子节点存放原始数据,内部节点存放聚合信息而已。每次修改数据以后,就从底部开始往根部调整聚合信息就可以了。
只是赢者树只是保存最值信息,而线段树扩展开来,在节点上可以加入数量,和值信息的维护。另外,普通的线段树用链表来实现,每个节点上都有自己的一个区间的left和right的信息。令人窒息的操作来了,当某个操作需要批量更新一个区间内的数据时,我们可以通过直接更新内部结点的数据来实现,而不需要回溯到叶子结点逐个更新,这就是线段树的惰性操作技巧。
如果我们有了一个标记标记这个线段的性质,那么为什么我们不在线段上加入一个是否有孩子的标记,这样我们就能动态开节点了,甚至是批量删除数据了,这就是动态线段树的技巧。但是,一旦允许动态开节点后,线段树就需要考虑到平衡的问题了,但它又不能像平衡树一样旋转。解决办法是引入替罪羊树的方法,加入约束条件,一旦不平衡就将树打平重建。
最后,线段树跟Splay树在区间操作的不同在于,它有批量操作,而且没有动态开点和删点操作时,代码会简单很多。
6.1.2 树状数组
树状数组,是简化版的线段树,可以代替线段树的数量和和值维护操作,具有空间更少,常数更少的优势。
假设,我们要维护一个能查询区间和值的线段树。那么,线段树的叶子结点就是原始数据数组,然后从内部结点开始到根结点开始聚合数据的和值。原来的数据长度为n时,就需要结点为2n的线段树。
\[ tree[x].sum = tree[x.left].sum+tree[x.right].sum \]
树状数组的想法是,在和值信息中,信息是没有丢失的,我们保存了左右子树的和值,就能知道该树的和值。反过来,我们保存了左子树和该树和值信息,就可以反向推导出右子树的信息。
那么,像线段树那样保存所有的左右子树,和该树的和值信息,就会造成空间冗余。我们完全可以只保留部分左子树的信息,以及该树的和值信息,至于右子树的信息,我们可以需要时再把它推导出来就可以了。所以,树状数组只保留了上述图中的C数据,没有A数据,也没有白色框的数据,空间复杂度降低到n。
void add(int x,int num){
for(;x<=n;x+=x&-x)
tree[x]+=num;
}那么,我们要在数据A[2]增加数值3时,不仅需要在C[2]增加3,也要在C[4]也增加3,C[8]也增加3,以此类推。
int sum(int x){
int answer =0;
for(;x>0;x-=x&-x)
answer+=tree[x];
return answer;
} 当我们需要统计前缀和的信息时,例如获取A[1…7]的信息时,我们需要叠加C[7],C[6]和C[4]的信息就可以了。
int get(int x){
return sum(x)-sum(x-1);
}
void set(int x,int num){
int inc = num - get(x);
add(x,inc);
}那么get和set的数据怎么做,按照sum反向推导出x数据,将set推导出inc再调用add就可以了。
要注意的是,树状数组无法维护最值信息,因为最值信息的聚合操作是信息丢失的,只维护根信息和左子树信息是无法反向推导出右子树信息的。而且,树状数组的区间操作是通过前缀信息聚合推导出来的,最值操作并不支持前缀信息聚合推导区间信息的。
6.1.3 ZKW线段树
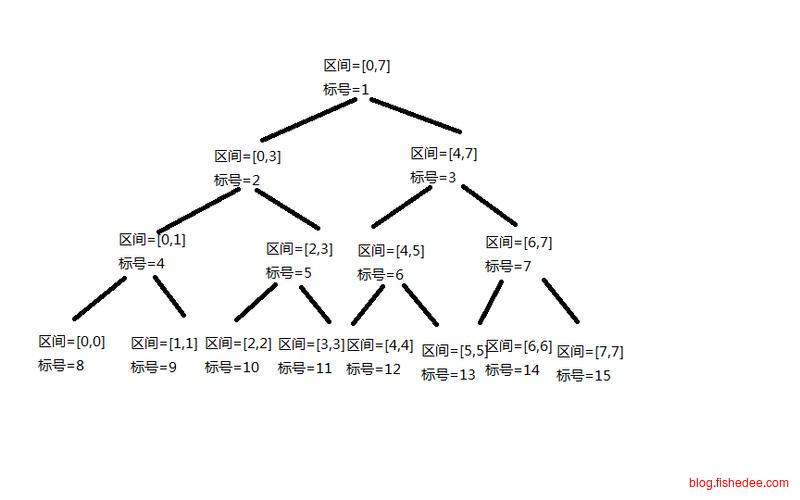
由于线段树的默认实现方式为链表,使用时常数比较大,大家就在考虑能不能用数组的方式来实现线段树。想法很简单,将数组开为2n的大小,然后原始数据放在[n…2n]的下标范围内,然后从底部开始往上的每个节点,通过[i/2]和[i/2+1]寻找到它的两个左右孩子,然后聚合数据就可以了(有一种借鉴了堆排序的完全二叉树的性质)。这样就能避免普通线段树的常数太大,又能像树状数组一样简单快速,实在牛逼,不过要注意,这样会失去动态开点和删点的能力了。
这个数据结构是由清华大学张昆玮发明的,他的统计的力量PPT很好地将平衡树,线段树,树状数组,分块哈希等联系起来,很有意思。
6.2 用途
线段树的使用方法有两种
6.2.1 下标
int get(int index);
void set(int index,int data);
void setRange(int index1,int index2,int data);
int getSum();
int getSumInRange(int index1,int index2);
int getMax();
int getMaxInRange(int index1,int index2);key为数组下标,统计数组区间内的最值,和和值。
6.2.2 值域
int get(int key);
void set(int key,int data);
void setRange(int key1,int key2,int data);
void add(int key,int data);
void del(int key);
void delRange(int key1,int key2);
int getSum();
int getSumInRange(int key1,int key2);
int getMax();
int getMaxInRange(int key1,int key2);
int getCount();
int getCountInRange(int key1,int key2);
int getKeyByRank(int rank);
int getRankByKey(int key);
int getKeyByRankInRange(int rank,int key1,int key2);
int getRankByKeyInRange(int key,int key1,int key2);
int getMode();
int getModeInRange(int key1,int key2);key为数据值域,统计数组区间内的值域信息,包括数量,最值和和值。要注意的是,这个时候叶子节点都有一个count字段,代表这个叶子节点的值域含有多少个这样的数据。这个时候就能实现删除数据了,就是在叶子节点将count字段设置为0就可以了。
这种方法也被称为权值线段树。
另外,当值域是静态浮点数或者范围很大时,你可以使用离散化的方式将值域转换为一个较小的整数范围内。如果数据是动态的浮点数时,就不能用离散化了,这个时候你可以上终极大招,用基数桶转换到一个整数范围就可以了。
- 本文作者: fishedee
- 版权声明: 本博客所有文章均采用 CC BY-NC-SA 3.0 CN 许可协议,转载必须注明出处!