1 概述
函数优化概览
最近像开了挂,机器学习中有很多以前看不懂的数学问题突然间都看明白了,当然,对于这些之前看不懂的问题,都是本科里面的基础问题了=,=,看懂了也不是什么牛逼的事。不得不说的是,当你看懂里面的推导的时候,你会发现,用数学来建模这个世界实在是太美妙了。
我之前看不懂这些数学推导,我总结了一下,其中的坎主要是:
- 基础知识不扎实,数学分析,概率论和线性代数一定都要懂,例如,要能清楚地知道\(P(X,Z;\theta)和P(X;Z,\theta)\)的区别,特征向量,正定矩阵等等这些一大堆的名词。
- 数学建模,要看懂机器学习的推导,关键是两点,理解如何用数学来表达这个问题,以及如何推导来解决这个问题。我之前一直都想不明白概率模型与分类之间究竟是怎么联系上的,混合高斯模型跟寻找图像中气球又他妈的是怎么勾搭上的。对我来说,怎么建模比怎么推导要难理解得多。千万不要直接跳过建模看算法,然后用直觉来理解算法,这样开始很好理解,但遇到后面就会卡壳,因为数学符号才是建模这个世界的最自然的语言,不理解数学符号要吃大亏。
- 一大堆的数学符号,不像普通理科书的推导,机器学习的数学推导,符号很多,很容易混乱,有些是参数,有些是常数,有些是标注数据,分清楚它们之间的区别很重要。另外,符号中遍及了很多的\(\sum \prod \mathop {argmax}_{x} f(x)\),它们是啥意思也要细心留意。
- 自变量不是x,机器学习大多数最后会将问题转化为求解模型的待定参数\(\theta\)的问题,这个时候\(\theta\)是自变量,Loss是因变量,我们要求的是Loss最小值问题。这跟一直以来都认为x是自变量,y是因变量的规范不太一样,这个傻逼的问题我曾困惑了很久。
2 建模
2.1 基础
2.1.1 分析
了解单元与多元积分与微分,偏微分方程
2.1.2 矩阵
了解矩阵运算(和,乘,逆),特征向量与特征矩阵,奇异矩阵与非奇异矩阵,实对称矩阵等等,矩阵结合导数和积分的计算。矩阵一般为竖立的写法。
2.1.3 概率
\[ P(Y) = \sum_{Z}P(Y,Z)\\ P(Y) = \sum_{Z}P(Y|Z)P(Z)\\ P(Y_1,Y_2,Y_3)=P(Y_1)P(Y_2|Y_1)P(Y_3|Y_1,Y_2)\\ P(Y|X) = \frac {P(Y,X)}{P(X)}\\ \]
了解随机变量的意义(不仅有值,还有概率分布),基础的概率公式,常见的概率分布,随机过程(随机过程实际就是输出为多个数值的随机变量),概率参数估计。
2.2 模型
2.2.1 形式化
这一步是最关键的一步,将问题用数学形式化地表达出来。问题的形式化分两步,一步是确定条件,另外一步就是确定目标。将问题数学形式化以后,然后用数学工具将条件推导到目标就可以了。
2.2.2 确定条件
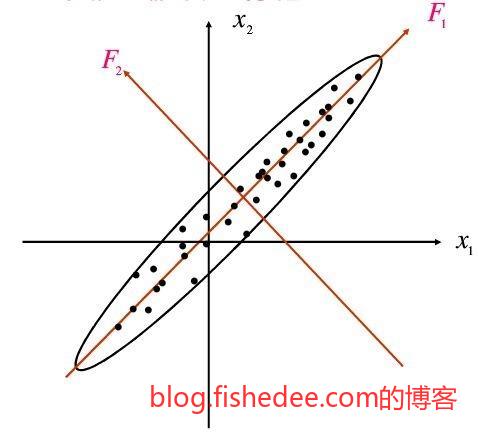
PCA主成分分析中,我们建模就是寻找一个线性变换使得重建误差最小。但是满足这样条件的线性变换很多,输出不唯一,PCA的简化在于,它要求线性变换后的基必须是单位正交的,这样大大简化了模型的复杂度,而且保证了输出结果的唯一性。
2.2.3 确定目标
不同的建模目标,会有不同的结果和计算量。
例如,我们手上有\((x_1,y_1),(x_2,y_2),...\)这么多的数据,我们需要找出一个\((x-a)^2+(y-b)^2=r^2\)的圆能最大限度地拟合它。
\[ Loss = \sum_{i=1}^{n}(\hat{y}_i-y_i)^2\\ =\sum_{i=1}^{n}(\sqrt{r^2-(x_i-a)^2}+b-y_i)^2 \]
我们可以以预计的y和实际的y之间作为差值作为损失,注意这个模型中需要求的参数是a,b和r,这三个参数才是自变量。当这样的模型不太漂亮,没有考虑到y值可能在圆的上方或下方的问题。
\[ 令g(x)=(x-a)^2+(y-b)^2-r^2\\ Loss = \sum_{i=1}^{n}(\hat{g}_i-g_i)^2\\ =\sum_{i=1}^{n}(\hat{g}_i)^2\\ =\sum_{i=1}^{n}[(x_i-a)^2+(y_i-b)^2-r^2]^2 \]
建立一个g(x),让g(x)的损失函数最小就是我们要求的那个圆了,这样建模后不再需要考虑在圆的上方或下方的问题,但是计算比较复杂。
\[ 令g(x)=x^2+y^2+cx+dy+e\\ Loss = \sum_{i=1}^{n}(\hat{g}_i-g_i)^2\\ =\sum_{i=1}^{n}(\hat{g}_i)^2\\ =\sum_{i=1}^{n}[x_i^2+y_i^2+cx_i+dy_i+e]^2 \]
我们将建模目标设置为一般方程后,既不再需要考虑在圆的上方或下方的问题,而且计算量要少很多。
2.3 目标
2.3.1 最小绝对损失法
\[ Loss = \lvert y-\hat{y} \rvert \]
通过最小化绝对误差来建模,但这个函数连续但是不可导,一般不会这么用。
2.3.2 最小二乘法
\[ Loss = (y-\hat{y})^2 \]
最小二乘损失,目标函数连续可导,是最常用的目标函数了。
2.3.3 极大似然估计
\[ P(X;\theta) = \frac {1} {1+e^{\theta^TX}} \]
极大似然估计,就是在已知概率模型的情况下,通过最大化已经发生事件的概率来估计参数。也就是
\[ \hat{\theta} = \mathop {argmax}_{\theta}P(X;\theta) \]
然后将已经观察到的\(P(y|X)\)代进去就可以了
2.3.4 最大后验估计
\[ P(\theta|x) = \frac {P(x|\theta)P(\theta)} {P(x)} \]
最大后验估计,就是在极大似然估计的基础上,考虑了参数\(\theta\)的先验分布
\[ \hat{\theta} = \mathop {argmax}_{\theta}P(x|\theta)P(\theta) \]
3 方程求根
3.1 二分法
\[ f(x)=0 \]
我们在已知f的情况下,求解x。
\[ 如果f是连续,而且f(x_1)f(x_2) <0\\ 那么x_1<x<x_2 \]
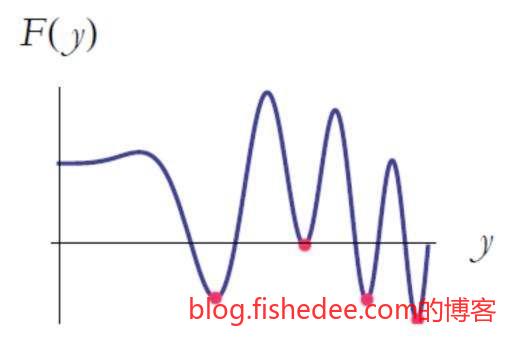
根据连续函数的介值定理,如果两个函数值的符号相反,那么肯定有一个根在其中。
\[ x_m = (x_1+x_2)/2\\ x=\begin{cases} x_1<x<x_m,f(x_1)f(x_m)<0\\ x_m<x<x_2,f(x_m)f(x_2)<0\\ \end{cases} \]
那么,我们可以通过二分的方法不断缩紧这个范围,显然,这个方法收敛的区间是对数式的。
3.2 牛顿法
\[ f(x)=0 \]
我们在已知f的情况下,求解x。
\[ f(x) = f(x_1)+f'(x_1)(x-x_1) \]
根据泰勒公式,在一个较小的\(x_1\)邻域内,我们可以将函数\(f(x)\)表示为一个线性函数。
\[ 0 = f(x_1) + f'(x_1)(x-x_1)\\ x = x_1 - \frac {f(x_1)}{f'(x_1)}\\ x^{n+1}=x^{n}-\frac {f(x^{n})}{f'(x^n)} \]
于是,我们推导出一条越来越接近\(f(x)=0\)的迭代公式,任取一个点\(x\),然后根据上面的迭代公式找到一个更加逼近根的解。这个方法称为牛顿迭代法。
要注意这种方法,要求根的位置导数不能为0,收敛速度是指数式的。而且,这个方法的特别之处在于它不需要步长参数,收敛快得飞起。
4 方程组求根
4.1 幂迭代法
\[ AX = X \]
我们在已知A的情况下,求解X。
\[ X^{n+1} = AX^{n} \]
幂迭代法的方法很简单,首先任意确定解空间,然后使用上面的迭代方法来逼近X,多步迭代以后就能解出X了。要注意的是,要求解的方程组本身要求有非零解才能使用以上的方法。
4.2 雅可比迭代
\[ AX = b \]
我们在已知A和b的情况下,求解X。

首先,我们将矩阵A分解为三个矩阵相加,下三角矩阵L,对角矩阵D,上三角矩阵U。那么\(A=L+D+U\)
\[ AX = b\\ (L+D+U)X = b\\ DX=-(L+U)X+b\\ X = -D^{-1}(L+U)X+D^{-1}b\\ 令B = -D^{-1}(L+U),C = D^{-1}b\\ 则X = BX+C\\ X^{n+1}=BX^{n}+C \]
那么,根据以上的迭代公式,我们就能和幂迭代法一样,先任意确定解空间,然后使用上面的迭代方法来逼近X,多步迭代以后就能解出X了。同样要注意的是,原来的矩阵A必须是非奇异矩阵才能使用。因为D是简单的对角矩阵,所以它的逆矩阵相当容易就能求解出来了。
4.3 高斯赛德尔迭代
\[ AX = b \]
我们在已知A和b的情况下,求解X。
\[ AX = b\\ (L+D+U)X = b\\ X = -D^{-1}(L+U)X+D^{-1}b\\ \]
高斯赛德尔迭代的公式跟雅可比迭代公式是一样的,唯一不同的是,雅可比迭代公式是每次迭代求解X的所有分量,高斯赛德尔迭代是每求解一个\(X^{n+1}\)的分量时,就替代当前\(X^n\)的分量中,来执行当前\(X^{n+1}\)的下一个分量计算,以更快地收敛。
4.4 牛顿法
\[ \begin{cases} f(x,y) = 0\\ g(x,y) = 0\\ \end{cases} \]
我们已知f和g的两个非线性函数,求解x和y。
\[ 令M(x,y) = f(x,y)\\ N(x,y) = g(x,y)\\ 则在某个较小的(x_0,y_0)邻域内,有\\ M(x,y) = M(x_0,y_0)+\begin{bmatrix} \frac {\partial M} {\partial x_0}\\ \frac {\partial M} {\partial y_0}\\ \end{bmatrix}^T\begin{bmatrix} x-x_0\\ y-y_0\\ \end{bmatrix}\\ N(x,y) = N(x_0,y_0)+\begin{bmatrix} \frac {\partial N} {\partial x_0}\\ \frac {\partial N} {\partial y_0}\\ \end{bmatrix}^T\begin{bmatrix} x-x_0\\ y-y_0\\ \end{bmatrix}\\ 合并后有:\\ \begin{bmatrix} M(x,y)\\ N(x,y)\\ \end{bmatrix}=\begin{bmatrix} M(x_0,y_0)\\ N(x_0,y_0)\\ \end{bmatrix}+\begin{bmatrix} \frac {\partial M} {\partial x_0} & \frac {\partial M} {\partial y_0}\\ \frac {\partial N} {\partial x_0} & \frac {\partial N} {\partial y_0}\\ \end{bmatrix}\begin{bmatrix} x-x_0\\ y-y_0\\ \end{bmatrix}\\ 也就是说\\ f(X) = f(X_0)+D(X-X_0) \]
注意,上面的矩阵D就是指雅可比行列式,问题等价于求\(f(X)=0\)时的根。就这样,我们将一个非线性方程组问题转化为一个线性方程组的问题。
\[ 0 = f(X_0)+D(X-X_0)\\ X = X_0-D^{-1}f(X_0)\\ X^{n+1} = X^{n} - (D^{n})^{-1}f(X^{n}) \]
因此,我们推导出了牛顿迭代法在多元线性方程组的迭代方程了,收敛速度依然是指数式的。但要注意的是,这个迭代方程需要求解雅可比行列式的逆,计算量比较大。
5 方程求最值
\[ f = f(x,y,z) \]
我们已知f函数的情况下,求解f最小值的x,y,z。也就是说,这是一个求最值的问题。当然,我们一般默认f的最值不在定义域边缘上,也就说不在[0,0,0]这些地方,而是在极值点上。求最值的问题被转化为一个求极值的问题。
5.1 坐标下降
\[ f(x_0+a,y_0+b,z_0+c)- f(x_0,y_0,z_0) <= A(a,b,c,x_0,y_0,z_0) \]
IIS的方法就是想办法建立一个不等式,\(f(x_0+a,y_0+b,z_0+c)\)是当前点更新后位置的函数值,\(f(x_0,y_0,z_0)\)是当前点位置的函数值,然后找出这两个函数值差值的上界A函数。
我们希望的是每一次迭代后\(f(x_0+a,y_0+b,z_0+c)\)都能尽可能少于\(f(x_0,y_0,z_0)\),也就说我们要求\(A(a,b,c,x_0,y_0,z_0)\)的极小值就可以了。因为\(A(a,b,c,x_0,y_0,z_0)\)取极小值时,\(f(x_0+a,y_0+b,z_0+c)-f(x_0,y_0,z_0)\)就有一个很低的上界,这保证了\(f(x_0+a,y_0+b,z_0+c)<f(x_0,y_0,z_0)\)。问题被转化为给另外一个函数\(A(a,b,c,x_0,y_0,z_0)\)的极小值的问题。
如果A函数比较简单,我们可以用拉格朗日方法一步得出极小值点,如果A函数比较复杂,我们就要进一步使用梯度下降,牛顿迭代等方法来寻找A的极小值点了。
但是,一般来说,很难找到同时让三个坐标都下降的a,b,c。我们会令b和c都是0,然后找到让A达到极小值点时的a值,也就是只让x坐标下降。然后令a和c都是0,然后找到让A达到极小值点时的b值,也就是只让y坐标下降。然后令a和b都是0,然后找到让A达到极小值点时的c值,也就是只让z坐标下降。总而言之,就是轮番着变更x,y,z的坐标,让总的函数值下降,而每次下降只变更一个下标,所以这种方法称为坐标下降法。
IIS方法是一种建立不等式来转化求其他极小值点函数的方法,一般用在原函数比较复杂,难以求解导数时使用。最大熵模型求解时就用到了IIS的思想
5.2 梯度下降
\[ f(x,y,z) = f(x_0,y_0,z_0)+\begin{bmatrix} \frac {\partial f}{\partial x_0}\\ \frac {\partial f}{\partial y_0}\\ \frac {\partial f}{\partial z_0}\\ \end{bmatrix}^{T}\begin{bmatrix} x-x_0\\ y-y_0\\ z-z_0\\ \end{bmatrix}\\ 令A=\begin{bmatrix} \frac {\partial f}{\partial x_0}\\ \frac {\partial f}{\partial y_0}\\ \frac {\partial f}{\partial z_0}\\ \end{bmatrix},X= \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix},X_0=\begin{bmatrix} x_0\\ y_0\\ z_0\\ \end{bmatrix}\\ 则f(x,y,z)=f(x_0,y_0,z_0)+A^{T}(X-X_0) \]
根据泰勒公式,我们推导出在\((x_0,y_0,z_0)\)的邻域附近满足上面的式子,我们希望的是找到一个\((x,y,z)\)使得\(f(x,y,z)<f(x_0,y_0,z_0)\),这相当于
\[ A^{T}(X-X_0)<0\\ X-X_0=-A\\ X=X_0-A \]
所以,我们推导出了梯度下降公式,只需要让X沿着当前梯度的反方向走就可以了。但是,由于这个方程只在\((x_0,y_0,z_0)\)的较小一个邻域满足,我们要求每一步都不能太大,所以需要一个额外的步长参数\(0<\lambda<1\),即
\[ X^{n+1}=X^{n}-\lambda A\\ X^{n+1}=X^{n}-\lambda \nabla f \\ \]
一般来说,\(\lambda\)都设置得比较小,为0.01这种。
为了解决朴素梯度下降收敛较慢的问题,衍生出动量梯度下降,Nestrov梯度下降等算法,在《深度学习入门实现》已经说过了,就不啰嗦了。
当然,梯度下降也不是万能的,如果这个点没有了梯度,它就会滞留在那里一动也不动。或者,它收敛到某一个极小值点时,它也会一动也不动。所以,梯度下降并不能保证收敛到全局的最小值点。但是,总的来说,梯度下降实现简单,每次迭代需要的计算量和空间都很小,收敛条件宽松,所以它仍然是目前大型神经网络的唯一优化算法。
5.3 牛顿法
\[ f(x,y,z) = f(x_0,y_0,z_0)+\begin{bmatrix} \frac {\partial f}{\partial x_0}\\ \frac {\partial f}{\partial y_0}\\ \frac {\partial f}{\partial z_0}\\ \end{bmatrix}^{T}\begin{bmatrix} x-x_0\\ y-y_0\\ z-z_0\\ \end{bmatrix}\\ +\frac {1} {2} \begin{bmatrix} x-x_0\\ y-y_0\\ z-z_0\\ \end{bmatrix}^{T}\begin{bmatrix} \frac {\partial f}{\partial^2 x_0} & \frac {\partial f}{\partial x_0\partial y_0} & \frac {\partial f}{\partial x_0\partial z_0}\\ \frac {\partial f}{\partial y_0\partial x_0} & \frac {\partial f}{\partial^2 y_0} & \frac {\partial f}{\partial y_0\partial z_0}\\ \frac {\partial f}{\partial z_0\partial x_0} & \frac {\partial f}{\partial z_0\partial y_0} & \frac {\partial f}{\partial^2 z_0}\\ \end{bmatrix}\begin{bmatrix} x-x_0\\ y-y_0\\ z-z_0\\ \end{bmatrix}\\ \]
根据泰勒公式的二阶展开式,我们推导出在\((x_0,y_0,z_0)\)的邻域附近满足上面的式子
\[ f(x,y,z)=f(x_0,y_0,z_0)+A^{T}(X-X_0)+\frac{1}{2}(X-X_0)^TB(X-X_0) \]
我们将其转化为矩阵形式,就是上面这个式子,其中B是一个矩阵,代表多元函数的二阶展开,称为Hessian矩阵。可以证明,当Hessian矩阵是正定时,导数为0的点就是极小值点。
\[ f'(x,y,z)=0 \]
也就是说,当我们已知Hessian矩阵是正定时,我们只需要求出导数为0的点就可以了。
\[ f(x,y,z)=f(x_0,y_0,z_0)+A^{T}(X-X_0)+\frac{1}{2}(X-X_0)^TB(X-X_0)\\ f'(x,y,z)=A+B(X-X_0)\\ 又f'(x,y,z)=0\\ 则0=A+B(X-X_0)\\ X=X_0-B^{-1}A\\ X_{n+1}=X_{n}-B_{n}^{-1}A_{n}\\ \]
就这样我们推导得到了牛顿法求极小值的方法,要注意这种方法需要Hessian矩阵是正定的,并且每次都需要求出Hessian矩阵的逆。另外,计算时不需要步长参数\(\lambda\),所以收敛非常快。
从另外一个角度考虑牛顿法求极小值,就是相当于求一阶导数为0的点。由于一阶导数是多个函数,也就是要求方程组的解。我们可以将这个方程组转化为雅可比阁行列式,然后用牛顿法求解这个方程组的根就可以了。而巧妙的是,一阶导数的雅可比阁行列式正好就是Hessian矩阵,所以两个截然不同的方法它们最终都指向到了牛顿法。因此,方程求根,方程组求根,方程求最值,都可以用同一个牛顿法来解决。
- 本文作者: fishedee
- 版权声明: 本博客所有文章均采用 CC BY-NC-SA 3.0 CN 许可协议,转载必须注明出处!