1 概览
组合优化概览
在机器学习中,处理序列问题上,HMM和CTC Loss都不约而同地用上了动态规划等等的组合优化技巧。于是,我顺道也把组合优化的问题都巩固了一遍。令人惊讶的是,组合优化的问题基本上都离不开四个套路。
- 搜索路径,是DFS,还是BFS,还是分治,不同的搜索路径有不同的剪枝策略。
- 记忆化,将局部状态保存下来,下次就不用再搜索一遍了。典型是动态规划,数据结构。
- 剪枝,在计算时利用关系特性,将没用的状态扔掉,达到减少搜索空间的效果。典型是动态规划求解LCS问题中引入单调队列,MinMax算法中\(\alpha-\beta\)剪枝,排序算法引用全序关系的传递性来剪枝,归并排序求逆序对问题也是引用全序关系的传递性来剪枝。
- 启发式,没有有效的最优化剪枝和记忆化策略时,我们引入近似算法,让搜索时尽量优先走更有可能的道路。典型是0-1背包的贪心算法,马跳棋盘的优先边缘算法,迷宫的A-Star算法。
2 搜索路径
2.1 DFS
走迷宫问题中,从出发点开始递归到走向终点。
2.2 反向DFS
走迷宫问题中,从终点开始递归到走向出发点。为什么要反向走,因为反向走的过程我们所需的递归过程很多。绝大部份的迷宫都是在出发点附近生成很多分支,而在终点附近的分支则很很少,反过来执行DFS,我们就能避免在开始时走到一些冤枉路去。例如,在海盗分金的问题上,从最后一个人开始考虑这个问题,比从开始第一个人考虑这个问题要简单得多。
2.3 BFS
在走迷宫的问题上,假设在每个分支点都分派多个老鼠来同时尝试这个通路,我们就能同时走向多个分支。很显然,这样的做法会让我们很容易找到最短路径是哪个。因为老鼠是同时派出的,最先到达的老鼠肯定就是最短路径导致的。
BFS的主要问题是它的剪枝策略比较麻烦,而且由于每个分支都分散老鼠,所以内存占有较大。
2.4 双向BFS
双向BFS重点解决的是单向BFS的内存占有太大的问题,在开始点和终点同时放出老鼠来搜索,当两个老鼠相遇时我们就找到了一条最短路径。可是,这个办法对于BFS来说依然是杯水车薪,减少的内存量不是特别明显。
2.5 分治法
无论DFS还是BFS,它们都是在开始点或者结束点开始搜索的,分治的想法是,为什么不从中间开始搜索。例如,在迷宫的问题上,如果我们找到一个必经点T,那么从A到B的搜索路径的问题就可以转化为:
- 从A到T
- 从T到B
不过,分治法处理迷宫问题效果不太明显,因为你很难一眼就知道迷宫的哪个点是必经点T。但是,在像排序,逆序对,最近点对的问题上,这个必经点T却是容易找出来的。
分治的一般步骤为:
- 拆解子任务,可以通过必经状态T来拆解,也可以通过规模来直接拆解。
- 解决子任务,这个就是递归本身,并没有什么好说的。
- 合并子任务的解,这一步可能有,可能没有,要看怎么分治。
另外,要注意的是,分治方法本身并没有一定能提高搜索效率,它关键在于:
- 拆解子任务,必经点拆解时必经点T是不是能有效率地完成,规模拆解时拆解的过程的是不是能有效率地完成。
- 合并子任务的解是不是能有效率地完成的
- 合并子任务的解时有没有使用相应的剪枝策略
2.5.1 按照规模拆解子任务
将规模n的问题固定划分为k个规模n/k的问题,从规模的角度来将问题缩减。
排序问题中,归并排序使用的是就是这种典型的想法,如果一个规模为n的序列,分为2个规模n/2的序列,如果这两个规模为n/2的序列都排好序后,我们就能用一个O(n)的算法将两个有序序列合并起来为一个规模为n的大序列。
另外,排序网路的问题中,双调排序使用的也是一样的想法,如果一个规模为n双调排序,我们进行前半与后半的一对一对应比较,那么前半部分和后半部分的位置就定下来了,而且这时的前半部分和后半部分都是双调序列。
注意,归并排序和双调排序都是按照规模拆解子任务,但归并排序是从下往上的,而双调排序是从上往下的。所以,并没有说按照规模拆解子任务就一定是从下往上进行的。
2.5.2 按照必经状态拆解子任务
将规模n的问题找出一个必经状态T,那么问题就能被划分为1…T,和T…N的两个问题。
排序问题中,快速排序就是这样的典型想法,随意找一个数字,然后将少于这个数字的放在左边,大于这个数字的放在右边,然后我们就能这个数字的最终确定位置了,而这个数字的位置就是必经状态T。
按照必经状态拆解子任务的主要问题是,必经点T可能导致分治的两个子问题并不均衡,运气不好的话会退化为原始DFS的效果。
2.5.3 合并子任务的剪枝
很多时候,分治本身并没有提高搜索的效率,但合并子任务的这个过程比较特别,我们可以引入剪枝来大幅优化。
给定一个序列包含n个数据{a1, a2, …, an},当i < j且ai > aj时,这两个元素构成一个逆序对,我们的问题是要求逆序对的数量。
count = 0;
for( i = 0 ; i < len ;i ++ ){
for( j = i+ 1 ; j < len ; j++ ){
if(a[i] >a[j]){
count++;
}
}
}简单的方法,就是dfs暴力搜索,所有状态搜索一遍。时间复杂度是\(O(n^2)\)
getResult(begin,end){
middle = (begin+end)/2;
count1 = getResult(begin,middle);
count2 = getResult(middle+1,end);
count3 = 0;
for( i = begin ; i <= middle ; i++ ){
for( j = middle + 1 ; j <= end ; j++ ){
if( a[i] > a[j] ){
count3 ++;
}
}
}
return count1+count2+count3;
}使用普通的分治后,逆序对的数量就是三部分,前半部,后半部,和前后部交叉。时间复杂度依然是\(O(n^2)\),没有任何改进。
getResult(begin,end){
middle = (begin+end)/2;
count1 = getResult(begin,middle);
count2 = getResult(middle+1,end);
sort(middle+1,end);
count3 = 0;
for( i = begin ; i <= middle ; i++ ){
j = binarysearch(a[i],middle+1,end);
count3 += end - j + 1;
}
return count1+count2+count3;
}但是,当分治引入剪枝策略就不一样了。因为逆序对需要满足两个条件,i < j和a[i] > a[j]。我们在合并子问题时,i<j的条件是肯定能满足的,我们要找的就只有a[i]>a[j]这一个条件而已。所以,我们可以将右半部分[middle+1,end]序列先从大到小排序,然后用二分搜索找出第一个比a[i]小的数字,我们就知道右半部分一共有多少个数字是少于a[i]的了。时间复杂度降低为\(O(n*log^2n)\)。如果我们进一步使用归并排序来加快右边的排序速度,时间复杂度能降低到\(O(n*logn)\)了。
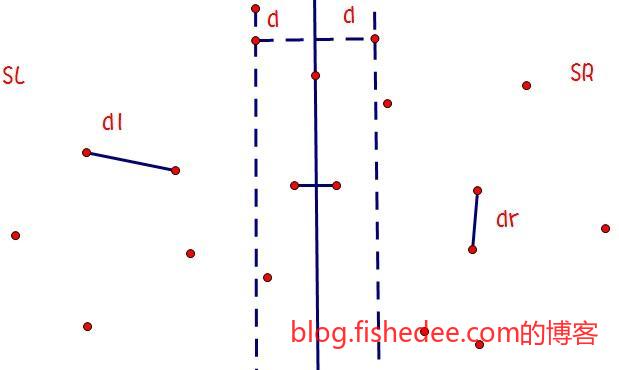
同样的道理,寻找平面中的最近点对也是一样的剪枝策略。我们要求的是\(min\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)。
getResult(begin,end){
middle = (begin+end)/2;
dis1 = getResult(begin,middle);
dis2 = getResult(middle+1,end);
dis3 = MAX;
for( i = begin ; i <= middle ; i++ ){
for( j = middle + 1 ; j <= end ; j++ ){
if( distance(a[i],a[j]) < dis3 ){
dis3 = distance(a[i],a[j]);
}
}
}
return min(dis1,dis2,dis3);
}简单的分治没有降低时间复杂度,依然为\(O(n^2)\)
getResult(begin,end){
middle = (begin+end)/2;
dis1 = getResult(begin,middle);
dis2 = getResult(middle+1,end);
minDis = min(dis1,dis2);
middlex = (a[middle].x+a[middle+1].x)/2;
for( i = begin ; i <= middle ; i++ ){
if( a[i] < middlex - minDis ){
continue;
}
for( j = middle + 1 ; j <= end ; j++ ){
if( a[j] > middlex + minDis ){
continue;
}
if( distance(a[i],a[j]) < minDis ){
minDis = distance(a[i],a[j]);
}
}
}
return minDis;
}
sort(a);
getResult(0,size(a));如果我们加入剪枝的策略,在合并的过程中,筛选掉那些,\[\lvert x_1-middle.x \rvert>minDis\]的点。因为这些点离中间点在横坐标上都太远了,距离肯定更远,不可能属于参与到最近点匹配中的。这样进行剪枝后期望的时间复杂度为\(O(n*logn)\)。但是,要注意变态的输入情况下,所有的点都是相同的横坐标,而纵坐标不同,这样会退化到没有剪枝的情况。解决方法是做空间四划分,同时在x轴和y轴上进行剪枝就可以了。
这两个例子都可以很有效的说明,分治本身并没有加快效率,我们还需要考虑加入剪枝策略。
3 记忆化搜索
3.1 状态记忆
状态记忆,就是在搜索的过程中将重复搜索子问题记忆下来,下一次在搜索时直接返回就可以了。
3.1.1 一维
getFib(n){
if(n == 1 || n == 2){
return 1;
}else{
return getFib(n-1)+getFib(n-2);
}
} 这是朴素的斐波拉契数列的解法,算法复杂度是指数式的,主要问题是不断搜索已经解决过的子问题,造成非常低效
getFib(n){
if( n == 1 || n == 2){
return 1;
}
if( cache[n] == -1 ){
cache[n] = getFib(n-1)+getFib(n-2);
}
return cache[n];
}使用cache作为缓存中间结果的数组后,时间复杂度下降到线性\(O(n)\)了
经典的LIS问题:求一个一维数组arr[i]中的最长递增子序列的长度,如在序列1,-1,2,-3,4,-5,6,-7中,最长递增子序列长度为4,可以是1,2,4,6,也可以是-1,2,4,6。注意,子序列的元素不需要是连续的。
result = -1
Lis(n,step){
result = max(result,step);
for( i = n -1 ; i >= 0 ; i++ ){
if( data[n] > data[i] ){
Lis(i,step+1)
}
}
}
for( i = 0 ; i != n ;i++){
Lis(i,1)
}最直接的方法是,使用dfs遍历所有可能的递增子序列,然后在最深层的循环中判断最大的长度,Lis(n)代表的是以第n元素结尾的最长递增子序列,时间复杂度为\(O(2^n)\)
Lis(n){
if(n==0){
return 1;
}
maxLen = 1;
for( i = n -1 ; i >= 0 ; i++ ){
if( data[n] > data[i] ){
maxLen = max(maxLen,Lis(i)+1)
}
}
return maxLen
}
result = -1
for( i = 0 ; i != n ;i++){
result = max(result,Lis(i))
}使用动态规划的想法,整体最优问题是不是包含着局部最优问题。在本题中,如果已知规模为n-1的LIS,我们就能轻易地知道规模为n的LIS,递推关系式为,\(dp[n]=max(dp[i]+1,1),if(data[i]<data[n])\)
Lis(n){
if(n==0){
return 1;
}
if( cache[n] != -1 ){
return cache[n];
}
maxLen = 1;
for( i = n -1 ; i >= 0 ; i++ ){
if( data[n] > data[i] ){
maxLen = max(maxLen,Lis(i)+1)
}
}
cache[n] = maxLen;
return maxLen
}
result = -1
for( i = 0 ; i != n ;i++){
result = max(result,Lis(i))
}看到这里,我们十分熟悉地看到类似Fib的问题,状态被不断重复的计算,这时候我们继续加入cache作为状态记忆后,时间复杂度下降到了\(O(n^2)\)。
使用状态记忆和动态规划的方法,它需要两个条件:
- 子问题重叠,搜索时不断重复同样的搜索路径,而这些路径是可以缓存起来给下一次使用的
- 最优子结构,整体最优结果是由各个局部最优结果组合起来的,我们不需要搜索所有的状态,我们只需要搜索所有局部最优的状态就可以了。
3.1.2 二维
平面上有N*M个格子,每个格子中放着一定数量的苹果。你从左上角的格子开始, 每一步只能向下走或是向右走,每次走到一个格子上就把格子里的苹果收集起来, 这样下去,你最多能收集到多少个苹果
getApple(n,m){
if( n == 0 && m == 0 ){
return data[n][m]
}
maxApple = -1
if(n-1>= 0){
maxApple = max(data[n][m]+getApple(n-1,m))
}
if(m-1>=0){
maxApple = max(data[n][m]+getApple(n,m-1))
}
return maxApple
}这个问题实际上要寻找的是最长权重的路径,而这条路径只能向下或者向右,递推公式也是很容易得到的。
getApple(n,m){
if( n == 0 && m == 0 ){
return data[n][m]
}
if( cache[n][m] != -1){
return cache[n][m]
}
maxApple = -1
if(n-1>= 0){
maxApple = max(data[n][m]+getApple(n-1,m))
}
if(m-1>=0){
maxApple = max(data[n][m]+getApple(n,m-1))
}
cache[n][m] = maxApple
return maxApple
}状态记忆的方法依然很简单,加个cache记录一下每一步能达到最大权重就可以了。
3.1.3 树
树形dp的问题一般是给定一棵树形关系给你,问如何删除或者增加树的节点,使得新的树在满足一定条件下值最大。例如,HDU1520,在一个有根树上每个节点有一个权值,每相邻的父亲和孩子只能选择一个。就是求如何删除树的节点,使得新树的总权值最大。
void dfs(int cur){
dp[cur][0]=0
dp[cur][1]=weight[cur];
for(int son=cur.first,son != cur.last ; son++){
dfs(son);
dp[cur][0] += max(dp[son][1],dp[son][0]);
dp[cur][1] += dp[son][0];
}
}
dfs(root)
result = max(dp[root][0],dp[root][1])这一道题是需要注意新树条件的,本节点如果选择的话,子节点就是不能选择的。本节点如果是没有选择的话,子节点是可以选择,也可以不选择的。
3.1.4 图
单源最短路径问题,给定一个带权有向图G=(V,E),其中每条边的权是一个实数。另外,还给定V中的一个顶点,称为源。现在要计算从源到目标的最短路径长度。
getShortDistance(cur,hasVisit){
if( cur == begin ){
return 0;
}
if( cache[cur][hasVisit] != -1 ){
return cache[cur][hasVisit];
}
hasVisit[cur] = true
distance = INT_MAX
for( v = cur.begin(); v != cur.end(); v++ ){
if( hasVisit[v.target] == true ){
continue;
}
distance = min(distance,getShortDistance(v.target,hasVisit)+v.weight)
}
hasVisit[cur] = false
cache[cur][hasVisit] = distance;
return distance
}
result = getShortDistance(end,{})在图的搜索中,经常出现的一个条件是每个点最多只能遍历过一次,所以,我们需要将hasVisit放入搜索的输入中,同时将hasVisit也放在cache中。注意,这个方法的时间复杂度依然为\(O(2^n)\)
3.2 条件记忆
我们有n种物品,物品j的重量为\(w_j\),价格为\(p_j\)。背包所能承受的最大重量为W。如果限定每种物品只能选择0个或1个,求如何选择使得背包的价格最大。
\[ max \sum_{j=1}^{n}p_jx_j\\ st. \sum_{j=1}^{n}w_jx_j \leq w\\ x_j \in \{0,1\} \]
用数学语言表示就是求以上的表达式
getMaxPackage(n,weight){
if( n == -1 || weight == 0 ){
return 0
}
if( cache[n][weight] != -1 ){
return cache[n][weight]
}
if( weight-w[n] >= 0 ){
choose = p[n]+getMaxPackage(n-1,weight-w[n])
}else{
choose = 0;
}
noChoose = getMaxPackage(n-1,weight)
cache[n][weight] = max(choose,noChoose)
return cache[n][weight];
}
result = getMaxPackage(n,W)在做状态记忆时,我们不能从只含规模n-1的问题就能推断到只含规模n的问题。因为,选择时的条件需要去考虑背包是否超重了,所以每个规模为n-1的问题中包含了多个当前剩余背包重量的不同分类。因此,我们也将剩余背包重量作为cache的一部分记忆起来了,这样才能有效地使用动态规划的方法。
3.3 状态压缩
3.3.1 集合状态
状态记忆时,像背包重量,规模数量都是一个整数,很容易就能作为一个索引保存在cache中。但是,像最短路径,旅行商问题中,会出现一个hasVisit的结构作为状态的一部分。
这个hasVisit的结构本身需要支持set的查找操作,同时也需要作为一个索引,放进cache里面,所以,它需要能被一对一地转化为一个整数。
解决方法就是状态压缩,将集合用一个数字表示,每个位置是否存在用对应的位是0还是1来决定就可以了。这样每个集合占用的空间少,而且存取的速度也很快。
3.3.2 大数状态
有时候状态是一个很大的整数,例如是31212312423,超过一个int32所能保存的空间,放在cache里面会很耗位置。但是,我们会注意到这个大数的最大数字只有4,那我们可以将这个数字转换为4进制就可以了,这样就能大大压缩状态的空间。
3.3.3 排列状态
状态是一个排列,例如87654321,和78654321等等,如果用大数保存,转换为8进制仍然需要一个int才能保存下来。但是8个数字的全排列总数量只有40320种,明显只需要一个short就能保存下来的。
这个特殊的状态可以用生成排列的思路来解决,将数字转换为特殊的进位制
\[ x_7*7!+x_6*6!+x_5*5!+x_4*4!+x_3*3!+x_2*2!+x_1*1!\\ x_7 \in \{0,1,2,3,4,5,6,7\}\\ x_6 \in \{0,1,2,3,4,5,6\}\\ ...\\ x_1 \in \{0,1\} \]
至于每个x的取值,则刚好就是这一位置第几大的数。例如\(x_7\)就是最高位第几大的数,例如,最高位是8,那么这个数就是第1大,所以为0,最高位是0,那这个数是第8大,所以为7。
4 搜索剪枝
搜索中的剪枝是一项化腐朽为神奇的工作,没有固定的套路,有时候时间复杂度没有变,有时候却下降到对数甚至线性上。
4.1 状态之间的关系
利用状态之间的关系,加快状态的搜索速度
4.1.1 逆序数对
getResult(begin,end){
middle = (begin+end)/2;
count1 = getResult(begin,middle);
count2 = getResult(middle+1,end);
sort(middle+1,end);
count3 = 0;
for( i = begin ; i <= middle ; i++ ){
j = binarysearch(a[i],middle+1,end);
count3 += end - j + 1;
}
return count1+count2+count3;
}原始的逆序数对中,采用了分治策略后时间复杂度依然为\(O(n^2)\),但是只要对右边的数组进行排序,然后用二分法找到对应的第一个比它大的数字,就能在\(log(n)\)的时间里找到这个数的所有逆向数对。那是因为
\[ 如果data[left]>data[right]且data[right]>data[k](k \in right)\\ 则data[left] > data[k]且left < k\\ 即left与k构成逆序数对 \]
排序后的剪枝策略将逆序数对的时间复杂度降低为\(O(n*log(n))\)
4.1.2 最短路径
getShortDistance(cur,hasVisit){
if( cur == begin ){
return 0;
}
if( cache[cur][hasVisit] != -1 ){
return cache[cur][hasVisit];
}
hasVisit[cur] = true
distance = INT_MAX
for( v = cur.begin(); v != cur.end(); v++ ){
if( hasVisit[v.target] == true ){
continue;
}
distance = min(distance,getShortDistance(v.target,hasVisit)+v.weight)
}
hasVisit[cur] = false
cache[cur][hasVisit] = distance;
return distance
}
result = getShortDistance(end,{})在我们刚才的最短路径问题中,我们使用了状态记忆的办法,将穷搜的时间复杂度\(O(n!)\)降低为\(O(2^n)\),但时间复杂度依然很高
\[ 如果v \in 已知最短路径的节点集,u \in 未知最短路径的节点集\\ 且distance[u_i]=min(edge[u_i][v_j]+distance[v_j]),v_j \in 已知最短路径的节点集v\\ 则i = \mathop argmin_{i}(distance[u_i])节点的最短路径就确定了 \]
剪枝的想法是这样的,u节点要么通过v节点集抵达起点,要么通过其他u节点集中的节点抵达到起点。对于前者,我们可以直接套用递推公式计算得到,对于后者,我们只能通过记忆化搜索得到。但是,剪枝策略告诉我们,只要某个节点\(u_j\)是所有节点u中最近能通过v节点集到达起点的,那么\(u_j\)肯定是不需要通过其他u节点集中的节点抵达到起点的。也就是说,通过这个操作后,我们每次能在O(n)时间内选择到一个最近的节点v。因此整个时间复杂度降低到了\(O(n^2)\)。要注意的是,这种剪枝策略要求节点间的权重是非负的。
4.1.3 双数和
一个很经典的题目,求指定在一个数组中,指定和为target的两个数字。
bool hasTwoSum(vector<int> data,int target){
for(int i = 0 ;i != data.size() ; i ++){
for(int j = i+1 ; j < data[i].size();j++){
if( data[i] + data[j] == target ){
return true;
}
}
}
return false;
}很显然,暴力的方法就是两层搜索,时间复杂度为\(O(n^2)\)
\[ data[i]+data[j]=target\\ st. 0<i<size\\ st. i<j<size\\ \]
在做优化之前,我们先将这个问题用数学的形式表达出来。
\[ \because data[i]+data[j]<target\\ data[k]<data[j]\\ \therefore data[i]+data[k]<data[i]+data[j]<target\\ \]
那么根据数学表达式,我们很容易找到一个关键。在内层循环中,如果某个j与i合并后少于target,那么比j少的数都不需要搜索了。反过来某个j与i合并后大于target,那么比j大的数都不需要搜索了。这样大大减少了我们需要查找数字数量。
int binary_search(vector<int> data,int begin, int end,first,target){
while( begin <= end){
int mid = (begin+end)/2;
if( data[mid]+first == target ){
return mid;
}else if( data[mid]+first < target ){
begin = mid+1;
}else{
end = mid-1;
}
}
return -1;
}
bool hasTwoSum(vector<int> data,int target){
sort(data.begin(),data.end());
for(int i = 0 ;i != data.size() ; i ++){
int j = binary_search(data,i+1,size()-1,data[i],target);
if( j != -1 ){
return true;
}
}
return false;
}那么,我们很直观地可以考虑先将数据排序,然后内层循环用二分法查找是否存在这个j不就可以了,时间复杂度为\(O(n*log(n))\)。注意,对于已经排序好的数组,这个方法的时间复杂度依然为\(O(n*log(n))\)
\[ \because data[i] + data[j] < target \\ data[i] <= data[k],\forall k\\ data[j] >= data[k],\forall k\\ \therefore data[i]+data[k]< data[i]+data[j]<target \]
我们在之前的方法时都是固定一个i,然后去寻找另外一个j。可是,如果我们在开始时就搜索i和j,情况就不一样了。我们选择i和j时尽可能选择剪枝效率最高的,让i指向当前数组的最小值,j指向当前数组的最大值。那么如果\(data[i]+data[j]<target\),我们就能推导出对于数组中任意的k,它和data[i]结合时都是必然少于target的。那么,我们直接从数组中剔除掉i就可以了。当然,情况反过来时,就剔除j。那么我们就能在剩余的数组继续套用这样的方法,不断取最小值和最大值。
bool hasTwoSum(vector<int> data,int target){
sort(data.begin(),data.end());
int i = 0;
int j = data.size()-1;
while(i < j ){
if( data[i]+ data[j]==target){
return true;
}else if( data[i] + data[j] < target){
i++;
}else{
j--;
}
}
return false;
}很显然,这样做的话,我们需要先将数组排序,然后取剩余数组的最小值和最大值时就能飞快地进行,总的时间复杂度为\(O(n*log(n))\)。注意,对于已经排序好的数组,这样做的时间复杂度为\(O(n)\)。
第一个方法就是暴力,第二个方法考虑到了状态之间的关系产生的剪枝,第三个方法则考虑到了如何选择搜索路径使得剪枝效率最高(也称为Two-Pointer方法),非常有趣!
4.2 状态与结果的关系
另外一种剪枝就是通过仔细检查状态,找出哪些对后续结果没有作用的最优子结构,那么后续进行递推时就能避免搜索如此多的最优子结构了。
result = -1
for( i = 0 ; i < n ; i++ ){
maxLen = 1
for( j = 0 ; j < i ; j ++ ){
if( data[i] > data[j] ){
maxLen = max(maxLen,dp[j]+1)
}
}
dp[i] = maxLen
result = max(result,maxLen)
}我们之前实现的LIS代码时间复杂度为\(O(n^2)\),我们先把它改为正序的形式。
\[ dp[i] = max(1,dp[j]+1)\\ st. j < i \\ st. data[j] < data[i] \]
从递推公式我们知道,我们每次的递推都是在寻找满足两个条件下的最大值。
\[ 如果data[k] > data[j]且dp[k] < dp[j]\\ 那么k就是一个无用状态\\ 因为如果k是组成LIS的一部分,那么选择j会是一个比该LIS更长的序列\\ 所以k不可能是组成LIS的一部分 \]
根据递推公式,我们可以逐步推导出以上的剪枝策略,寻找到一些无用状态。那么,我们可以用一个队列来只维护那些有效的状态。
\[ 如果i<j\\ 则data[i]<data[j]且dp[i]<dp[j] \]
一旦只维护有效状态后,这个队列就会满足以上这个关系式,也就是这个队列是单调的。既然如此,我们就能用二分法来查找到每一步的最佳选择,而不需要遍历所有可能。
result = -1
for( i = 0 ; i < n ; i++ ){
j = binearysearch(data[i],queue)
if( j == -1 ){
dp[i] = 1;
}else{
dp[i] = dp[j]+1
}
result = max(result,dp[i])
for( k = j ; k < n ; k++ ){
if( dp[queue[k]] > dp[queue[j]] ){
break;
}
}
if( k == j ){
queue[j] = i;
}else{
queue[j] = i;
for( o = j+1,l = k ; l < n ; l++ ,o++){
queue[o] = queue[l]
}
}
}就这样,经过剪枝后,LIS的时间复杂度降低到\(O(n*log(n))\)了。
result = -1
for( i = 0 ; i < n ; i++ ){
j = binearysearch(data[i],queue)
if( j == -1 ){
dp[i] = 1;
}else{
dp[i] = dp[j]+1
}
result = max(result,dp[i])
for( k = j ; k < n ; k++ ){
if( dp[queue[k]] > dp[queue[j]] ){
break;
}
}
queue[j] = i;
}在这个问题中,其实还可以进一步剪枝,因为队列中的dp每次都是新增一的,所以肯定比插入位置的dp值相同,比前一个位置少一。所以不需要对后面的数据进行遍历的。
4.3 数据结构
在搜索的过程中,我们总是需要做一个取计数或者最值的过程
4.2.1 查找
\[ data[j] = target-data[i]\\ st. i < j < size\\ \]
双数和的内层循环中,我们可以考虑其实是一个查找数据的问题。很显然,我们可以用能快速查找数据的数据结构来加速这个过程,但有一个\(i<j\)的条件,我们需要注意动态地维护这个数据结构。
bool hasTwoSum(vector<int> data,int target){
unordered_set<int> hash;
for( int i = 0 ;i != data.size();i++){
hash.insert(data[i]);
}
for( int i = 0 ; i != data.size();j++){
hash.erase(data[i]);
bool isExist = hash.exist(target-data[i]);
if( isExist ){
return true;
}
}
return false;
}能做查找的数据结构,有二叉树,有哈希表,有基数树等等,我们这里用哈希表,因为它的期望时间复杂度最优,快到为\(O(1)\),所以整个过程的时间复杂度为\(O(n)\),是这个问题的理论最优时间复杂度。当然,对于已经排序好的数组而言,TwoPointer方法才是最优的,常数最小,最坏情况下时间复杂度依然为\(O(n)\)。
4.3.2 计数
result = 0;
for( i = 0 ; i < n ; i++ ){
count = 0;
for( j = 0 ; j < i ; j ++ ){
if( data[i] > data[j]){
count++;
}
}
result += count;
}在朴素的逆序数对中,时间复杂度为\(O(n^2)\)
\[ count(j)\\ st. j < i \\ st. data[j] > data[i] \]
因为在二层循环中,我们需要不断进行上述的操作来计数满足条件的j。如果我们能找到一个数据结构能快速完成以上的操作来能更快地完成整个计数
\[ count(j)\\ st. data[j] > data[i] \]
对于平衡树,我们加上size的统计字段后,我们就能在\(log(n)\)时间内执行以上操作,但逆序对是两个条件,不是一个条件的呀,怎么办。解决办法是让平衡树的数据是动态插入进去不就可以了。
result = 0;
for( i = 0 ; i < n ; i++ ){
count = tree.count(data[i])
result += count;
tree.add(data[i]);
}就这样,通过数据结构,我们完成了逆序对的\(O(n*log(n))\)时间复杂度下加速。要注意的是,通过动态插入数据来实现其中一个条件是一个常见而且重要的技巧。
4.3.3 最值
result = -1
for( i = 0 ; i < n ; i++ ){
maxLen = 1
for( j = 0 ; j < i ; j ++ ){
if( data[i] > data[j] ){
maxLen = max(maxLen,dp[j]+1)
}
}
dp[i] = maxLen
result = max(result,maxLen)
}原始的Lis算法时间复杂度也是\(O(n^2)\)的
\[ max(dp[j])\\ st. j < i \\ st. data[j] < data[i] \]
原因还是在在第二层循环中,求解最大值的时间复杂度为\(O(n^2)\)
\[ max(dp[j])\\ st. data[j] < data[i] \]
对于以上这个式子来说,我们可以用平衡树或者线段树来优化使得时间复杂度降低到\(O(log(n))\),但Lis中还需要一个\(j<i\)的条件,解决办法跟上一节一样,让数据是动态输入就可以了
result = -1
for( i = 0 ; i < n ; i++ ){
maxLen = segtree.get(data[i])
dp[i] = max(1,maxLen+1)
result = max(result,maxLen)
segtree.set(data[i],dp[i])
}上面使用的是线段树的方法,一般会将数据离散化再放进去,这样能大幅减少线段树所需的空间。
5 启发式搜索
5.1 贪心
设有n个正整数,将它们连做成一排,组成一个最大的多位整数。例如n=3时,3个整数123,312,343,连成的最大整数为34331213。又如:n=4时,4个整数7,13,4,246,连成的最大整数为7424613.
很显然,这个方法可以用dfs来解决。不过这样的时间复杂度也太高了\(O(n!)\)。即使用上了动态规划,时间也在\(O(2^n)\)。
但是,我们直观地能感受到以343为开头的数字,肯定比123为开头的数字要更好,也就是说,如果每一步中我们只需看剩余数字中最佳选择的单个选择就可以了,不需要全局地看最佳选择是什么。
for( i = 0 ; i < n ; i++ ){
int max = i;
for( j = i + 1 ; j < n ; j++ ){
if( int(data[j]) > int(data[max])){
max = j;
}
}
swap(data[max],data[i])
}所以,我们直观地选择数值最大的优先。但是这样做并不能保证是全局最优的。例如,12,121的组成数字中,按照这样的算法得出结果是121,12,但正确答案应该是12,121。按照这样的贪心策略,我们能得出一个接近全局最优的结果,也是一种启发式策略了。时间复杂度为\(O(n^2)\)
for( i = 0 ; i < n ; i++ ){
int max = i;
for( j = i + 1 ; j < n ; j++ ){
if( data[j]+data[max] > data[max]+data[j]){
max = j;
}
}
swap(data[max],data[i])
}如果换个角度来考虑,我们可以用剪枝策略,我们在每一层选择时就能剪枝了,不需要递归到最深时才去剪枝,这样我们就能在\(O(n^2)\)时间复杂度上得到全局最优的结果。
5.2 A-Star
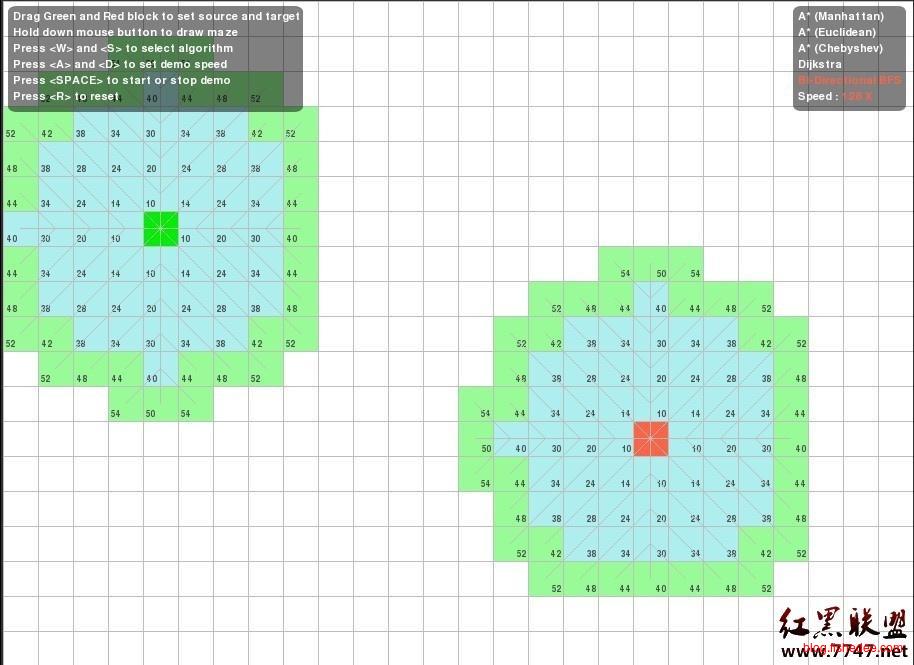
我们的目标是找到一条从狗到骨头的最短路径,显然,我们可以用BFS来解决这个问题,但是BFS的宽度优先方式太占用内存里,找到目标时几乎已经遍历了整张地图。
所以,我们希望能在较小内存的情况下,找到一条接近最短的路径。
我们在探索路径时,需要在队列中找到下一个可行的方块,在BFS和DFS中这个选择都是很随意的,BFS是当前深度最小的方块,DFS是当前深度最大的方块。一个直观的想法是,我们希望优先选择那些离开始点和终点最近距离的下一个方块。可是,开始点距离在不同路径过来时不一样的,终点距离更扯,没到达终点时终点距离更是无法算出来的。
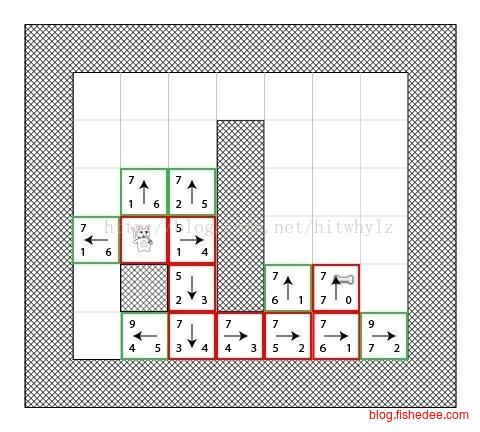
A*算法的想法是,我们用一个启发式的想法来逼近开始点距离G和终点距离H。开始点距离就选目前所走过路径中能最快到达该方块的距离,终点距离就选当前方块到终点的曼哈顿距离(也就是在忽略所有障碍物时的终点距离)。
将方块添加到open列表中,该列表有最小的和值。且将这个方块称为S吧。
将S从open列表移除,然后添加S到closed列表中。
对于与S相邻的每一块可通行的方块T:
如果T在closed列表中:不管它。
如果T不在open列表中:添加它然后计算出它的和值G+H。
如果T已经在open列表中:当我们使用当前生成的路径到达那里时,检查G+H和值是否更小。如果是,更新它的和值和它的前继。由于有启发式的选择下一个方块的策略,A*算法能在比BFS更小内存速度更快的情况下,找到一个接近最短路径的逻辑方法。这种使用优先队列的启发式策略,我们可以套在马走日,八皇后的问题上。
6 总结
组合优化看起来就像是一种智力题,但是套上了数学模型后,就变得有套路可循了,很是有意思。1
- 本文作者: fishedee
- 版权声明: 本博客所有文章均采用 CC BY-NC-SA 3.0 CN 许可协议,转载必须注明出处!