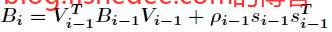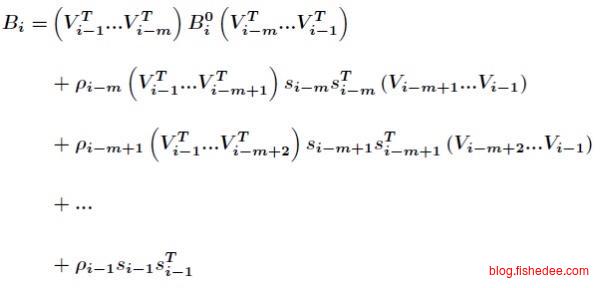6 梯度下降变种
\[ X^{n+1}=X^{n}-\lambda \nabla f^{n} \]
这是朴素的梯度下降实现,\(f^{n}\)是第n次迭代时的梯度,\(X^{n}\)是第n次的变量,\(X^{n+1}\)是第n+1次的变量,\(\lambda\)是学习率。
由于朴素的梯度下降算法严重依赖于\(\lambda\)的设置,设置得太大收敛会很快,但是容易造成震荡不收敛。设置得太小收敛会很慢,但不容易造成震荡。所以,提出了多种的梯度下降的变种来解决这个问题。
6.1 衰减梯度下降
\[ \lambda^{n}=\frac {\lambda}{1+n\cdot decay}\\ X^{n+1}=X^{n}-\lambda^{n} \nabla f^{n} \]
所以,衰减梯度下降的想法是,让学习率随着迭代次数增加而下降,方法随着迭代次数增加而增大分母,从而减少\(\lambda^{n}\),这个方法称为倒数衰减梯度下降。
\[ \lambda^{n}=\begin{cases} \lambda,n<=100\\ decay \cdot \lambda,n>100\\ \end{cases}\\ X^{n+1}=X^{n}-\lambda^{n} \nabla f^{n} \]
另外一些更加简单暴力的做法,就是设定在多少次以后直接降低学习率,这个方法称为逐步衰减梯度下降。实践表明,这个方法简单暴力的方法相当有效。
6.2 动量梯度下降
\[ \nabla g^{n} = \nabla g^{n-1} \times discount +\nabla f^{n}\\ X^{n+1}=X^{n}-\lambda \nabla g^{n} \]
动量梯度下降从另外一个角度解决收敛的问题,就是下降梯度。朴素的梯度下降使用的是该位置的一阶导数方向,当我们设置\(\lambda\)过低时,收敛就会过慢,但是就能避免震荡。
\[ \because \nabla g^{n} = \nabla g^{n-1} \times discount +\nabla f^{n}\\ \nabla g^{n-1} = \nabla g^{n-2} \times discount +\nabla f^{n-1}\\ ...\\ \nabla g^{2} = \nabla g^{1} \times discount +\nabla f^{1}\\ \therefore \nabla g^{n} = \nabla g^{n-1} \times discount +\nabla f^{n}\\ = (\nabla g^{n-2} \times discount +\nabla f^{n-1}) \times discount +\nabla f^{n}\\ = ((\nabla g^{n-3} \times discount +\nabla f^{n-3}) \times discount +\nabla f^{n-2}) \times discount +\nabla f^{n}\\ ...\\ = \nabla f^{1} \times discount^{n}+\nabla f^{2} \times discount^{2}+...+\nabla f^{n-1} \times discount^{1}+\nabla f^{n} \]
动量梯度下降,它本质上就是将多个一阶导数进行指数叠加,来生成当前的梯度方向。越靠近当前位置的导数权重越大,越远离当前位置的导数权重越小。这造成了当最近的多次一阶导数方向一致时,那么当前的梯度方向就会下降得比较快,如果最近的多次一阶导数方向不一致时,那么当前的梯度方向就会下降得比较慢。这样,只需要将\(\lambda\)设置为一个较小的数值,也能达到快速收敛而且不震荡的效果。
6.3 Nestrov梯度下降
\[ \nabla f^{n+1} = \nabla f(X^{n}-\lambda \times \nabla g^{n-1} \times discount)\\ \nabla g^{n} = \nabla g^{n-1} \times discount +\nabla f^{n+1}\\ X^{n+1}=X^{n}-\lambda \nabla g^{n} \]
动量梯度下降中不仅考虑了当前的一阶导数,还考虑了最近位置的一阶导数。但是,在拐点的位置,也就是最低点附近,由于动量的存在,会造成过度动量超过折返动量,所以在最低点附近收敛过慢。
Nestrov梯度下降的想法,使用未来位置的一阶导数来考虑当前的梯度,而不是现在这个位置的一阶导数来考虑当前的梯度。那么,在下一步到达拐点时,由于看到了未来的一步会造成折返动量,所以,当前位置就会提前减速,避免过分越过最低点的问题。
所以Nestrov梯度下降比动量梯度下降在最低点附近收敛得更快。
7 牛顿法变种
\[ X_{n+1}=X_{n}-H_{n}^{-1}g_{n}\\ \]
朴素牛顿法求解最值问题时,需要将函数的二阶导数,也就是Hessian矩阵算出来,然后求Hessian矩阵的逆矩阵。它的优点在于不需要考虑步长,而且收敛非常快,缺点是计算量太大,求Hessian矩阵的逆实在太慢了。所以,提出了多种牛顿法变种来解决这个问题。
注意,牛顿法的使用前提是Hessian矩阵是正定的。
7.1 DEP法
\[ f_{n+1}=f_{n}+g_n^{T}(X_{n+1}-X_n)+\frac{1}{2}(X_{n+1}-X_n)^TH_{n}(X_{n+1}-X_n)\\ \nabla f_{n+1} = g_n+H_{n}(X_{n+1}-X_n)\\ g_{n+1}=g_n+H_{n}(X_{n+1}-X_n)\\ g_{n+1}-g_n=H_{n}(X_{n+1}-X_n)\\ \Delta Y_{n} = H_{n} \Delta X_n \]
从上面这个推导方程我们可以得知,Hessian矩阵就是一阶导数差值和自变量差值的比值,也就是导数的导数,即二阶导数。
那么,我们在用牛顿法时,关键在于需要每次都要按照函数本身求二阶导数,即Hessian矩阵,同时也要算出它的逆。为什么,我们不从导数的导数定义本身来求出Hessian矩阵呢。也就是算出这两个位置的导数,以及位置的变化值,反过来推导出Hessian矩阵呢。这样就能避免需要从函数本身求二阶导数的复杂性。
7.1.1 相邻位置代替
可是,我们用牛顿法的本身,就是为了从Hessian矩阵中求解出一阶导数为0的点呀。如果我已经知道了一阶导数为0的点,为什么还需要求解Hessian矩阵呢。这进入了一个鸡生蛋,蛋生鸡的死循环中。
\[ \Delta Y_{n} = H_{n} \Delta X_n\\ \Delta Y_{n} = B_{n+1} \Delta X_n \]
打破这个循环的关键在于,我们使用第n个位置的Hessian矩阵作为第n+1个位置的Hessian矩阵的估计值。因为相邻的两个位置,它们的二阶导数都是差不多的呀,那就直接近似使用吧。那么,我们可以先从\(X_n\)和\(Y_{n}\)作为下一个点的近似二阶导数\(B_{n+1}\),然后从\(X_{n+1}\)和\(B_{n+1}\)算出\(Y_{n+1}\),然后从\(X_{n+1}\)和\(Y_{n+1}\)作为下一个点的近似二阶导数\(B_{n+2}\),直到\(Y_{n+k}\)的一阶导数为0为止。
7.1.2 求逆近似
好了,现在我们解决了减少计算Hessian矩阵的问题,但是,Hessian矩阵的求逆的计算量依然在那里,我们依然少不了。
\[ H_{n}^{-1} \Delta Y_{n} = \Delta X_n\\ G_{n+1} \Delta Y_{n} = \Delta X_n \]
解决办法就是,我们直接一步近似计算出Hessian矩阵的逆就好了,不要迂回计算Hessian矩阵的逆。要从\(Y_{n}\)和\(X_n\)近似计算出Hessian矩阵的逆,我们的\(G_{n+1}\)要满足两个条件:
- 满足\(G_{n+1} \Delta Y_{n} = \Delta X_n\)
- 满足正定性
推导如下:
\[ G_{n+1} \Delta Y_{n} = \Delta X_n\\ 令G_{n+1} = G_{n}+P_{n}+Q_{n}\\ G_{n+1}\Delta Y_{n} = G_{n}\Delta Y_{n}+P_{n}\Delta Y_{n}+Q_{n}\Delta Y_{n}\\ 要让G_{n+1} \Delta Y_{n} = \Delta X_n\\ 则可以让P_{n}\Delta Y_{n}=\Delta X_n且Q_{n}\Delta Y_{n} =-G_{n}\Delta Y_{n}\\ 那么让P_{n} = \frac {\Delta X_n \Delta X_n^{T}}{\Delta X_n^{T}\Delta Y_{n}}\\ Q_{n} = -\frac {G_{n}\Delta Y_{n}\Delta Y_{n}^{T}G_{n}}{\Delta Y_{n}^{T}G_{n}\Delta Y_{n}}\\ 即可 \]
那么
\[ G_{n+1} = G_n + \frac {\Delta X_n \Delta X_n^{T}}{\Delta X_n^{T}\Delta Y_{n}} -\frac {G_{n}\Delta Y_{n}\Delta Y_{n}^{T}G_{n}}{\Delta Y_{n}^{T}G_{n}\Delta Y_{n}} \]
就能既满足等式,又能满足正定性了。那么,我们只要开始时随便设定一个正定的矩阵\(G_n\),之后的Hessian矩阵的逆\(G_{n+1}\)就能从这个等式中计算出来了。不需要求逆,也不需要计算二阶导数。
说实话,刚看到这个推导时,我是懵逼的,为什么这样都能行,看着好像可以,但就是好像哪里说不通。那是因为,这简单的几个等式中充满了函数优化中常见的trick!
7.1.3 奇技淫巧
\[ G_{n+1} \Delta Y_{n} = \Delta X_n\\ \]
首先,我们要让\(G_{n+1}\)满足上面这个等式
\[ G_{n+1} = \frac {\Delta X_n \Delta X_n^{T}}{\Delta X_n^{T}\Delta Y_{n}} \]
我们发现只需要这么构造\(G_{n+1}\)就好了,注意这里的构造过程是分子是一个矩阵,分母是一个数字。当我们将这个\(G_{n+1}\)放入\(Y_{n}\)时,刚好分子可以用矩阵的乘法结合律,使得分子的后面可以和分母相约掉,达到等于等式右边的能力。
但是,只有这个等式是不行的,因为\(Y_{n}\)和\(X_n\)都是一个向量,满足这个等式的\(G_{n+1}\)的矩阵有无限多个。我们希望从中选出一个不仅满足这个等式,而且是正定的。
\[ G_{n+1} = G_{n}+P_{n}+Q_{n} \]
我们的想法是将\(G_{n+1}\)从\(G_{n}\)和我们刚才的一起构造出来,这样既能满足等式,又能被正定的\(G_{n}\)传染使得是正定的。
\[ P_{n}\Delta Y_{n}=\Delta X_n\\ Q_{n}\Delta Y_{n} =-G_{n}\Delta Y_{n} \]
注意这样的构造法,第二项是为了构造出满足等式,第三项是为了和第一项抵消。这里可能会有疑问,既然\(Q_{n}\Delta Y_{n} =-G_{n}\Delta Y_{n}\),那么\(Q_{n}=-G_{n}\)了么,然后\(G_{n+1} = G_{n}+P_{n}+Q_{n}=G_{n}+P_{n}-G_{n}=P_{n}\),不就是和之前的构造法一样的么。
这里的关键在于当\(Q_{n}\Delta Y_{n} =-G_{n}\Delta Y_{n}\)时,\(Q_{n}\neq-G_{n}\),因为\(Q_{n}\)的构造方法并不只一种,只和单变量计算时是不一样的!
所以,经过这样构造出来后
\[ G_{n+1} = G_{n}+P_{n}+Q_{n}\\ = G_n + \frac {\Delta X_n \Delta X_n^{T}}{\Delta X_n^{T}\Delta Y_{n}} -\frac {G_{n}\Delta Y_{n}\Delta Y_{n}^{T}G_{n}}{\Delta Y_{n}^{T}G_{n}\Delta Y_{n}} \]
\(G_{n+1}\)就能满足两个条件了,但是这种构造依然是近似性的,因为这两个条件只是Hessian矩阵的必要条件,而不是充分条件。在多元空间中,你是无法只根据一阶导数和自变量就能推导出二阶导数出来的。
\[ G_{n+1} = G_{0}+P_{n}+Q_{n}\\ = G_0 + \frac {\Delta X_n \Delta X_n^{T}}{\Delta X_n^{T}\Delta Y_{n}} -\frac {G_{n}\Delta Y_{n}\Delta Y_{n}^{T}G_{0}}{\Delta Y_{n}^{T}G_{0}\Delta Y_{n}} \]
其实,即使\(G_{n+1}\)这样构造也是能满足两个条件的,只是近似得不太准确而已。
7.2 BFGS法
\[ H_{n}^{-1} \Delta Y_{n} = \Delta X_n\\ G_{n+1} \Delta Y_{n} = \Delta X_n \]
我们知道DEP法是使用\(G_{n+1}\)近似\(H_{n}^{-1}\)的,这样就能实现近似计算,和避免求逆。
\[ \Delta Y_{n} = H_{n}\Delta X_n\\ \Delta Y_{n} = B_{n+1} \Delta X_n \]
那么,BFGS的方法就是用\(B_{n+1}\)来近似\(H_{n}\)的,无可避免的在我们求出\(B_{n+1}\)后仍然需要求逆,但BFGS找到了一个神奇的办法解决了这个问题。
\[ B_{n+1} \Delta X_{n} = \Delta Y_n\\ 令B_{n+1} = B_{n}+P_{n}+Q_{n}\\ B_{n+1}\Delta X_{n} = B_{n}\Delta X_{n}+P_{n}\Delta X_{n}+Q_{n}\Delta X_{n}\\ 要让B_{n+1} \Delta X_{n} = \Delta Y_n\\ 则可以让P_{n}\Delta X_{n}=\Delta Y_n且Q_{n}\Delta X_{n} =-B_{n}\Delta X_{n}\\ 那么让P_{n} = \frac {\Delta Y_n \Delta Y_n^{T}}{\Delta Y_n^{T}\Delta X_{n}}\\ Q_{n} = -\frac {B_{n}\Delta X_{n}\Delta X_{n}^{T}B_{n}}{\Delta X_{n}^{T}B_{n}\Delta X_{n}}\\ 即可 \]
首先,我们推导出\(B_{n+1}\),和DEP法就是差不多的技巧而已。
\[ B_{n+1}=B_{n}+\frac {\Delta Y_n \Delta Y_n^{T}}{\Delta Y_n^{T}\Delta X_{n}}-\frac {B_{n}\Delta X_{n}\Delta X_{n}^{T}B_{n}}{\Delta X_{n}^{T}B_{n}\Delta X_{n}} \]
好了,我们现在有了\(B_{n+1}\)了
\[ (A+uv^T)^{-1}=A^{-1}-\frac {A^{-1}uv^TA^{-1}}{1+v^TA^{-1}u} \]
求\(B_{n+1}\)的逆时,使用的是Sherman-Morrison公式,它可以将矩阵和的逆分解为两个矩阵的逆。那么,我们可以将\(B_{n+1}\)矩阵看成是三个矩阵的和,然后应用两次Sherman-Morrison公式,就能得到
\[ B_{n+1}^{-1}=(I-\frac{\Delta X_n\Delta Y_n^T }{\Delta X_n^T\Delta Y_n})B_{n}^{-1}(I-\frac{\Delta X_n\Delta Y_n^T }{\Delta X_n^T\Delta Y_n})^{T}+\frac {\Delta X_n\Delta X_n^T}{\Delta X_n^T\Delta Y_n} \]
好了,我们现在就得到了\(B_{n+1}^{-1}\)的迭代公式了,那么,我们在迭代时就能使用这个BFGS公式直接迭代就可以,不需要先求\(B_{n}\),再求它的逆了。实践证明,这个方法的迭代精确度比DEP法要好很多。
7.3 Broyden法
\[ G_{n+1}^{DEP}=G_{n+1} = G_0 + \frac {\Delta X_n \Delta X_n^{T}}{\Delta X_n^{T}\Delta Y_{n}} -\frac {G_{n}\Delta Y_{n}\Delta Y_{n}^{T}G_{0}}{\Delta Y_{n}^{T}G_{0}\Delta Y_{n}}\\ G_{n+1}^{BFGS}=B_{n+1}^{-1}=(I-\frac{\Delta X_n\Delta Y_n^T }{\Delta X_n^T\Delta Y_n})B_{n}^{-1}(I-\frac{\Delta X_n\Delta Y_n^T }{\Delta X_n^T\Delta Y_n})^{T}+\frac {\Delta X_n\Delta X_n^T}{\Delta X_n^T\Delta Y_n}\\ G_{n+1}^{Broyden}=\alpha G_{n+1}^{DEP}+(1-\alpha)G_{n+1}^{BFGS} \]
既然DEP法和BFGS法都是逆牛顿法的对偶形式而已,Broyden就将它们加权组合起来吧,就这么简单,其中\(0<=\alpha<=1\)
7.4 L-BFGS法
无论是DEP法,还是BFGS法,都需要存储\(G_{n}\),一个空间为\(O(n^2)\)的矩阵,LBFGS的想法是让\(G_{n+1}\)进一步做一个近似,同时减少空间占有量。
原始的BFGS公式,注意图中的\(B_{i+1}\)其实近似的是Hessian矩阵的逆,而不是Hessian矩阵本身。
那么,它的前一次迭代就是
将两个公式代入,相当于求得向前两步的迭代公式。
如果,我们不断地套入,就能得到一个往前k步的迭代公式。然后我们将第n-k次的矩阵\(B_{n-k}\)用某一个固定正定矩阵\(B_0\)近似代替就可以了,那么空间中只需要保存k步里面的\(s,t\)就可以了。每个\(s,t\)都是一个n维的向量,共k步,所以空间复杂度为\(O(k*n)\)。
LBFGS是大规模优化问题中的拟牛顿法的基础算法。
8 凸二次规划
\[ f(X) = \frac {1} {2} X^TAX+b^TX\\ g = f'(X) = AX+b\\ H = f''(X) = A \]
我们将求最值的目标局限在一个二次函数\(f(X)\)中,而且它的系数矩阵A是正定的,我们称这个问题为凸二次规划问题。
\[ AX + b = 0 \]
显然,这个函数的导数就是\(AX+b\),它的Hessian矩阵为\(A\)是正定的,那么导数为0的点就是极小值点,刚好就是我们要求的优化目标。而且由于矩阵A是正定的,那么它就是满轶的或者叫非奇异的,这个解X就是唯一的。换句话说,这个凸二次规划的解只有一个,刚好就是在导数为0的极值点上。
为了求解这个方程,我们需要将A矩阵求逆,但这样做的话计算量太大了。或者用方程组求解的方式来近似计算,但是这样做又太慢了,没有有效地利用它的满轶性质。所以,我们希望找到一个方法能更快地解决这个问题,而且又要精确的。
8.1 最速梯度下降
\[ X^{n+1}=X^{n}-\lambda \nabla f \\ \lambda = \mathop {argmin}_{\lambda}f(x^{n}-\lambda \nabla f) \]
最速下降法的想法是在朴素梯度下降的基础上,将\(\lambda\)设置为当前梯度方向上函数值最小的点。
\[ g_t = AX_t+b\\ g_t^Tg_{t+1}=0 \]
从最速梯度下降的定义中,我们可以进一步推导出,相邻两轮迭代的梯度肯定相互正交。因为如果不正交,那么\(g_{t+1}\)就可以分解一部分分量到\(g^{t}\)的方向,使得\(g^{t}\)不是\(\mathop {argmin}_{\lambda}f(x^{n}-\lambda \Delta f)\)了。要注意的是,这个性质只是说相邻梯度相互正交,没有说所有梯度相互正交,这个定义是存在多轮下降中梯度会重叠方向的,因为最速梯度下降只是当前梯度方向的最小值而已。
\[ g_t^Tg_{t+1}=0\\ g_t^T(AX_{t+1}+b)=0\\ g_t^T(A(X_t-\lambda g_t)+b) = 0\\ g_t^T(AX_t+b) - g_t^TA\lambda g_t = 0\\ g_t^Tg_t - g_t^TA\lambda g_t = 0\\ \lambda = \frac {g_t^Tg_t} {g_t^TAg_t} \]
就这样的,我们将步长推导出来了,相当简单。
呃,至于收敛性嘛,这是一个复杂的问题,可以证明,收敛速度跟A矩阵的特征值有关,矩阵A的最大最小特征值差距越小,收敛越快。
最速梯度下降每次都是选择梯度方向上函数值最小的点,但是有可能多次下降过程中都在同一个方向上反复上升下降,导致总的迭代次数过多。
8.2 共轭梯度下降
8.2.1 向量分解
\[ X^{n+1}=X^{n}-\lambda \nabla f^{n}\\ X^{n}=X^{n-1}-\lambda \nabla f^{n-1}\\ ...\\ X^{2}=X^{1}-\lambda \nabla f^{1}\\ X^{n+1}=X^{n}-\lambda \nabla f^{n}\\ =X^{1}-\lambda \nabla f^{1}-\lambda \nabla f^{2}-...-\lambda \nabla f^{n} \]
我们可以看到\(X^{n+1}\)的迭代其实就是\(X^{1}\)叠加多个梯度合成出来的。
\[ X^* = \alpha_1d_1+\alpha_2d_2+...+\alpha_nd_n=\sum_{i=1}^{n}\alpha_id_i\\ \]
所以,一个很自然的想法是,我们需要求解的\(X^*\)最终也是一个n维向量,所以它肯定可以分解为n个线性无关的向量组叠加。这样分解的原因就是,我们最多只需要求出n个系数\(\alpha_i\)就可以了,不需要像梯度下降一样迭代很多次。求解取函数最小值时的X,被转化为,求解取函数最小值时的\(\alpha_i\),当然,线性无关向量组\(d_i\)是任意取的,只需要线性无关就可以了。
8.2.2 系数求解
\[ f(X) = \frac {1} {2} X^TAX+b^TX\\ =\frac {1} {2}(\sum_{i=1}^{n}\alpha_id_i)^TA(\sum_{i=1}^{n}\alpha_id_i)+b^T(\sum_{i=1}^{n}\alpha_id_i)\\ =\frac {1} {2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jd_i^TAd_j+b^T(\sum_{i=1}^{n}\alpha_id_i) \]
我们发现推导到这里就推导不下去了,因为,这个函数的偏导数我们依然很难求出来,求出来以后也难解。
\[ d_i^TAd_j=0,i\neq j \]
那么,我们就在线性无关的向量组\(d_i\)上动主意,让这个向量组的向量不仅线性无关,而且相互是共轭正交的,也就是满足上面的这个式子。
\[ f(X)=\frac {1} {2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jd_i^TAd_j+b^T(\sum_{i=1}^{n}\alpha_id_i)\\ =\frac {1} {2}\sum_{i=1}^{n}\alpha_i^2d_i^TAd_i+b^T(\sum_{i=1}^{n}\alpha_id_i)\\ \frac {\partial f}{\partial \alpha_i} =\alpha_id_i^TAd_i+b^Td_i\\ \]
这个时候,我们就能很容易地得出偏导数
\[ \alpha_id_i^TAd_i+b^Td_i=0\\ \alpha_i=-\frac {b^Td_i}{d_i^TAd_i} \]
好了,我们现在知道了,当找到一组共轭的线性无关向量组以后,我们就能求出对应的系数\(\alpha_i\)了。那么,这个问题的就剩下最后一个了,如何找到一组共轭的线性无关向量组。
8.2.3 共轭方向求解
\[ 输入:\{u_1,u_2,...,u_n\}\\ 输出:\{d_1,d_2,...,d_n\}\\ \]
我们在线性代数中学习过向量正交化的方法——Gram-Schmidt方法,可以将一组线性无关的向量组转换为一组正交的向量组。那么,我们是否可以用类似的方法,将一组线性无关的向量组转换为转换为一组共轭正交的向量组呢。
\[ d_1 = u_1\\ d_2 = u_2+\beta_{2,1}d_2\\ d_3 = u_3+\beta_{3,1}d_2+\beta_{3,2}d_3\\ ...\\ d_i = u_i+\sum_{j=1}^{i-1}\beta_{i,j}d_j\\ \]
Gram-Schmidt的分解方法
\[ d_k^TAd_i=0,(k<=i)\\ d_k^TA(u_i+\sum_{j=1}^{i-1}\beta_{i,j}d_j)=0\\ d_k^TAu_i+\sum_{j=1}^{i-1}\beta_{i,j}d_k^TAd_j=0\\ d_k^TAu_i+\beta_{i,k}d_k^TAd_k=0\\ \beta_{i,k}=-\frac {d_k^TAu_i}{d_k^TAd_k} \]
好了,我们代入进去后,就能求得共轭方向构造的系数了,相当奇妙。现在,只要给我们一组线性无关的向量组,就能构造出对应的一组共轭方向向量组了。那么,共轭梯度下降至此就能算出来了。
8.2.4 梯度无关向量组
按道理来说,共轭梯度下降这个问题就已经解决完了。但是,我们还不满足,因为在构造共轭方向向量组时,我们需要计算\(O(n^2)\)个\(\beta_{i,k}\)个构造系数,我们希望找一组便利的线性无关的向量组,使得大部分的\(\beta_{i,k}\)都为0,这样我们计算量就能少很多了。
\[ g_{k+1}^Tg_{i}\\ =(AX_{k+1}+b)g_{i}\\ =(A(X_{k}+\alpha_k d_k)+b)g_{i}\\ =(AX_{k}+b+\alpha_k d_k^TA)g_{i}\\ =(g_{k}+\alpha_k d_k^TA)g_{i}\\ =g_{k}g_{i}+\alpha_k d_k^TAg_{i}\\ d_k^TAg_{i} = \frac {1}{\alpha_k}(g_{k+1}^Tg_{i}-g_{k}g_{i})\\ \]
我们得到了一个\(d_k^TAg_{i}\)的公式,刚好就是\(\beta_{i,k}\)的分子。我们发现将梯度作为线性无关向量组,有很特别的性质。
\[ \beta_{i,k}=-\frac {d_k^TAg_i}{d_k^TAd_k}\\ = \frac {1}{\alpha_k}\frac {(g_{k+1}^Tg_{i}-g_{k}g_{i})}{d_k^TAd_k}\\ =\begin{cases} \frac {1}{\alpha_k}\frac {(g_{i}^Tg_{i})}{d_k^TAd_k},k+1=i\\ 0,k+1<i\\ \end{cases} \]
就这样,我们得到一个非常化简的式子,将梯度作为线性无关向量组时,就只有一个\(\beta\)是有值,其他都是0。
就这样,整个共轭梯度优化就完成了,以梯度方向作为基础向量组,然后用类似Gram-Schmidt的方法转换为共轭方向,再乘以对应的\(\alpha\),组合起来就可以了。它可以保证最多只需要n次迭代就能找到最优值,非常牛逼。
10 总结
函数优化的套路:
- 泰勒公式,将函数用泰勒公式近似为线性或二次函数,然后分别用对应的梯度下降或牛顿法来优化。
- lambda优化,针对梯度下降的学习率进行优化,最速下降法,衰减梯度下降都属于这个范畴。
- 梯度优化,针对梯度下降的方向或大小进行优化,动量梯度下降针对大小进行优化,共轭梯度下降针对方向进行优化。
- 牛顿法变种,和共轭梯度下降中都包含有技巧性的trick。
- 本文作者: fishedee
- 版权声明: 本博客所有文章均采用 CC BY-NC-SA 3.0 CN 许可协议,转载必须注明出处!