10 储能元件
10.1 电容
10.1.1 电流与电压关系
\[ q(t)=Cv(t)\\ i(t)=C\frac {dv(t)}{dt}\\ v(t) = \frac {1} {C}\int_{-\infty}^{t}i(t)dt \]
在电容中,电荷量和电压是累积量,电流是瞬间量
10.1.2 能量关系
\[ w_E(t) = \frac {q^2(t)}{2C} = \frac {Cv^2(t)}{2} \]
电容中的能量计算,那肯定是和当前的累积量有关了
10.1.3 串联与并联
\[ \frac {1} {C} = \frac {v(t)}{q(t)} = \frac {v_1(t)+v_2(t)} {q(t)}= \frac {v_1(t)}{q(t)} + \frac {v_2(t)}{q(t)} = \frac {1}{C_1} + \frac {1} {C_2} \]
串联电容的时候,两个电容的电荷量总是相同的。所以,电容值的倒数为分别的电容值的倒数之和。
\[ C = \frac {q(t)} {v(t)} = \frac {q_1(t)+q_2(t)}{v(t)} = \frac {q_1(t)} {v(t)} + \frac {q_2(t)} {v(t)} = C_1 + C_2 \]
并联电容的时候,两个电容的电压总是相同的。所以,电容值为分别的电容值之和。
10.2 电感
10.2.1 电流与电压关系
\[ \lambda = Li(t)\\ v(t) = L\frac {di(t)}{d(t)}\\ i(t) = \frac {1} {L}\int_{-\infty}^{t} v(t)dt \]
在电感中,电感值和电流值都是累积量,电压是瞬间量
10.2.2 能量关系
\[ w_M(t) = \frac {\lambda^2(t)}{2L} = \frac {Li^2(t)}{2} \]
电感中的能量计算,那肯定是和当前的累积量有关了
10.2.3 串联与并联
\[ L = \frac {\lambda(t)} {i(t)} = \frac {\lambda_1(t)+\lambda_2(t)}{i(t)} = \frac {\lambda_1(t)} {i(t)}+\frac {\lambda_2(t)}{i(t)} = L_1+L_2 \]
串联电感的时候,两个电感的电流值总是相同的。所以,电感值为分别的电感值之和。
\[ \frac {1} {L} = \frac {i(t)} {\lambda(t)} = \frac {i_1(t)} {\lambda(t)}+\frac {i_2(t)} {\lambda(t)} = \frac {1} {L_1}+\frac {1}{L_2} \]
并联电感的时候,两个电感的电压相同,所以它们有相同的电感值。所以,电感值的倒数为分别的电感值的倒数之和。
10.3 简单电路
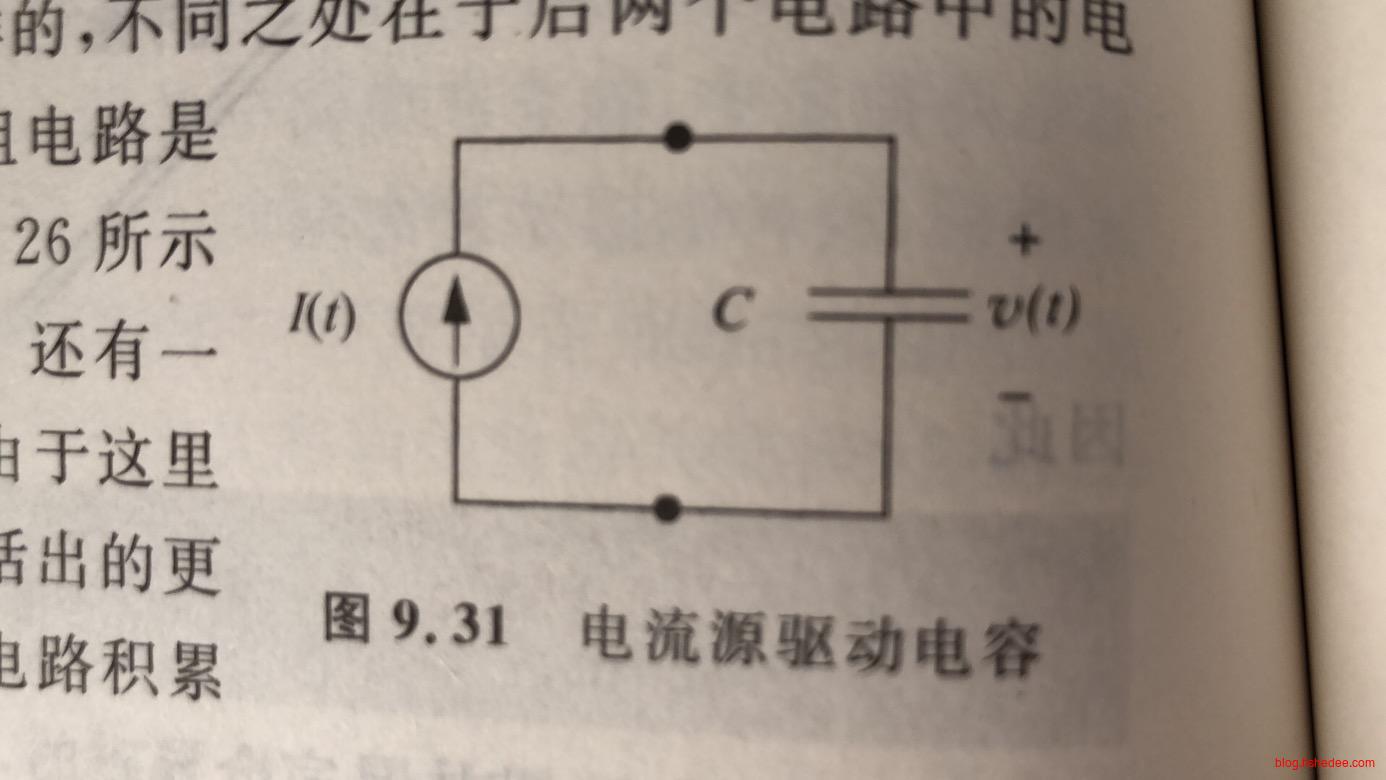
10.3.1 电流源驱动电容
电容电流已经知道了,就是\(I(t)\),我们需要从\(I(t)\)推导出\(v(t)\)。
\[ v(t) =\frac{1}{C}\int_{-\infty}^t I(t)dt \]
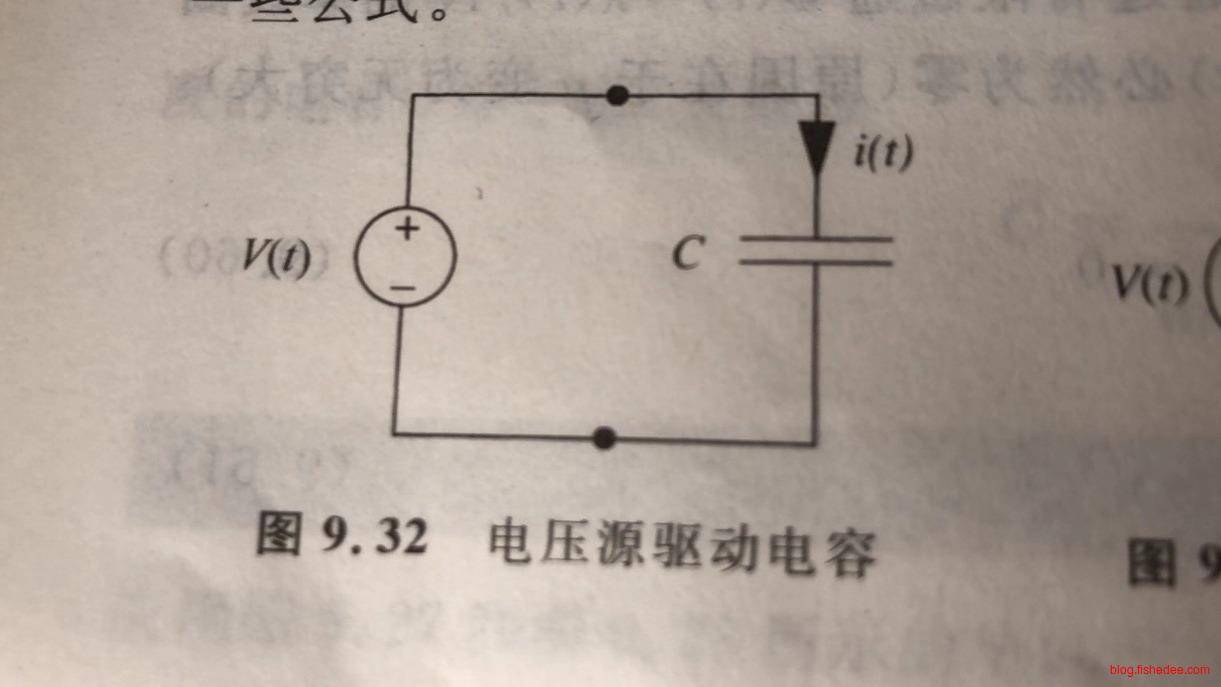
10.3.2 电压源驱动电容
电容电压已经知道了,就是\(V(t)\),我们需要从\(V(t)\)推导出\(i(t)\)。
\[ i(t) = C\frac {dV(t)} {dt} \]
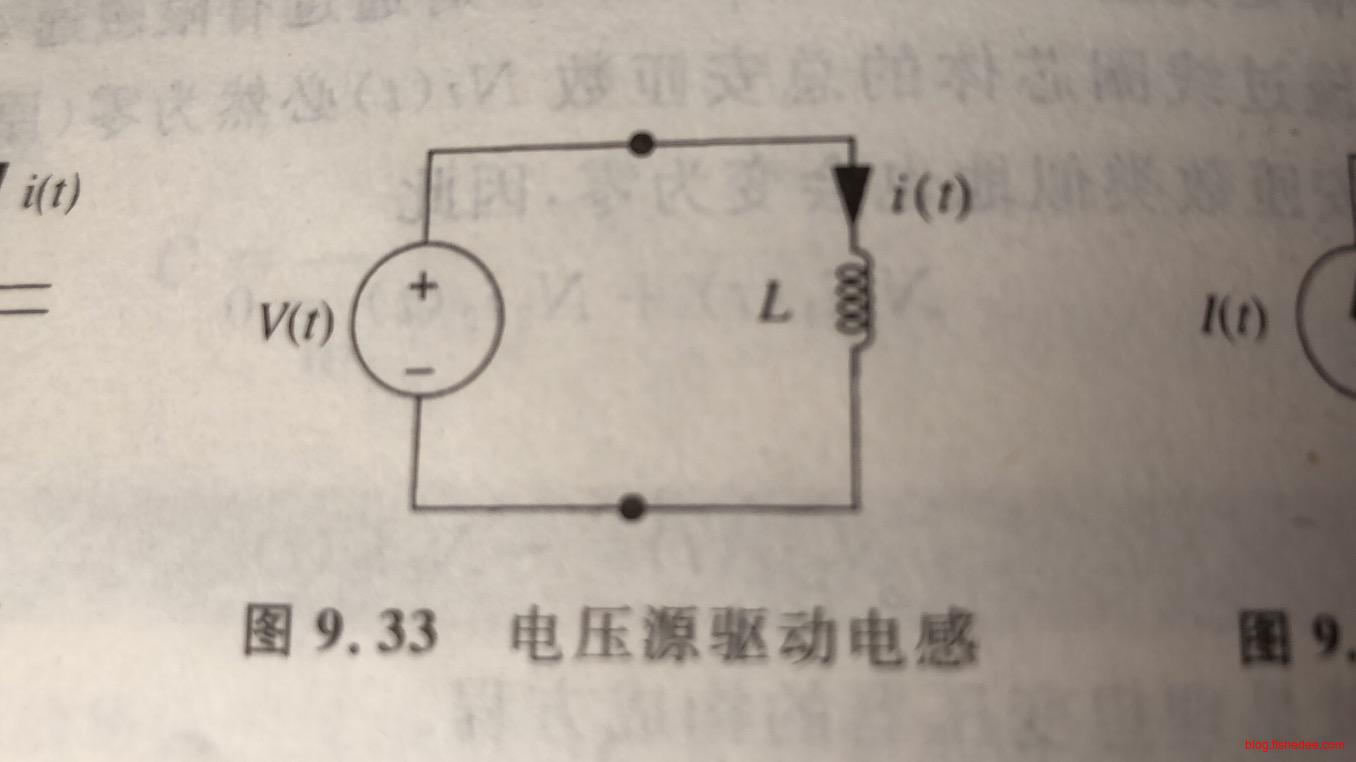
10.3.3 电压源驱动电感
电感电压已经知道了,就是\(V(t)\),我们需要从\(V(t)\)推导出\(i(t)\)。
\[ i(t) = \frac {1} {L} \int_{-\infty}^t V(t)dt \]
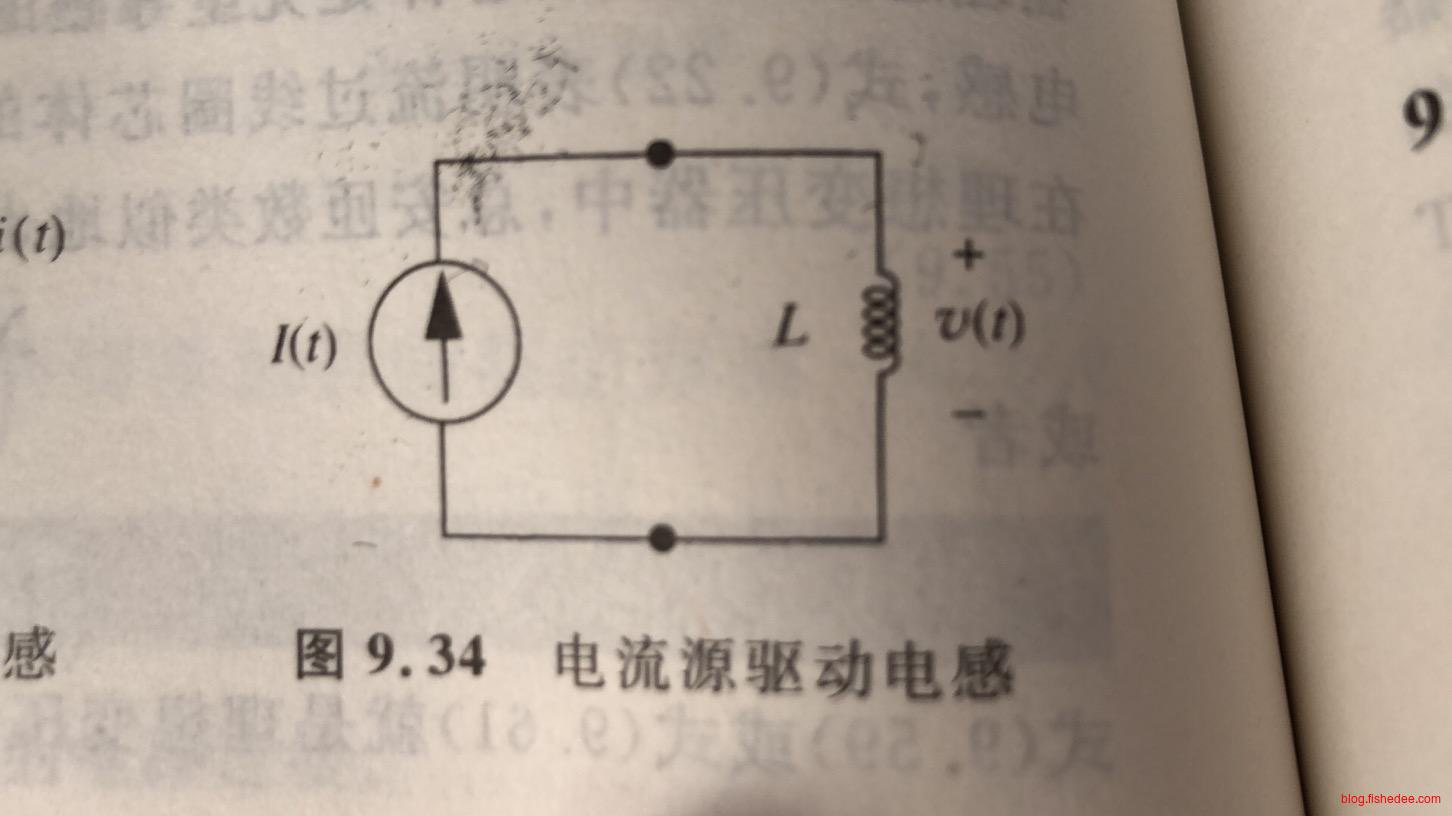
10.3.4 电流源驱动电感
电感电流已经知道了,就是\(I(t)\),我们需要从\(I(t)\)推导出\(v(t)\)。
\[ v(t) = L \frac {dI(t)}{dt} \]
10.4 跃阶输入
10.4.1 电流源驱动电容
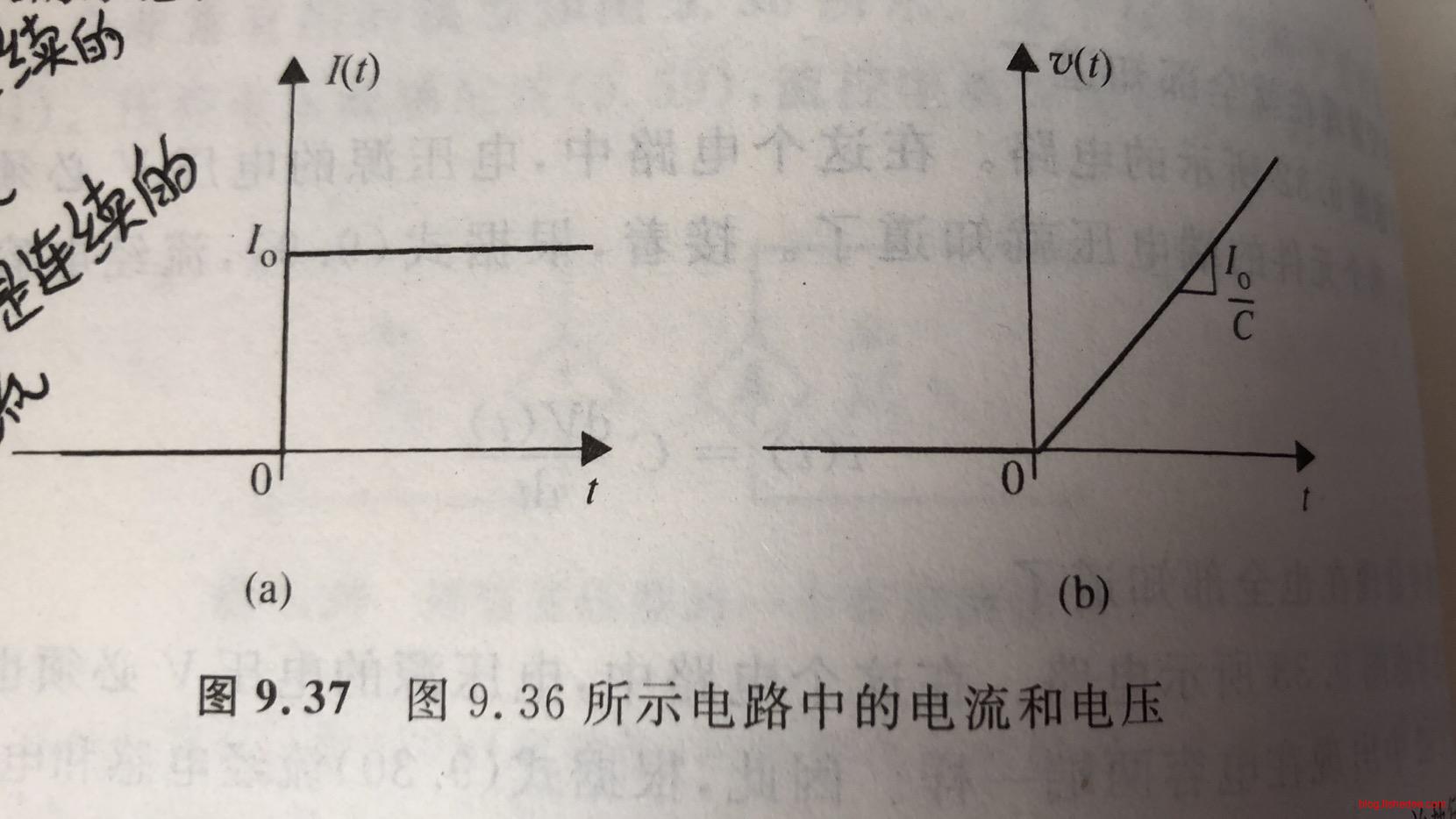
\[ I(t) = \begin{cases} 0,t\leq 0\\ I_0,t\gt 0\\ \end{cases} \]
当电流源是跃阶输入,就是以上方程的时候,根据公式
\[ v(t) =\frac{1}{C}\int_{-\infty}^t I(t)dt\\ v(t) = \begin{cases} 0,t \leq 0\\ \frac {I_0t}{C},t\gt 0\\ \end{cases} \]
得到\(v(t)\)是一个线性函数
10.4.2 电压源驱动电容
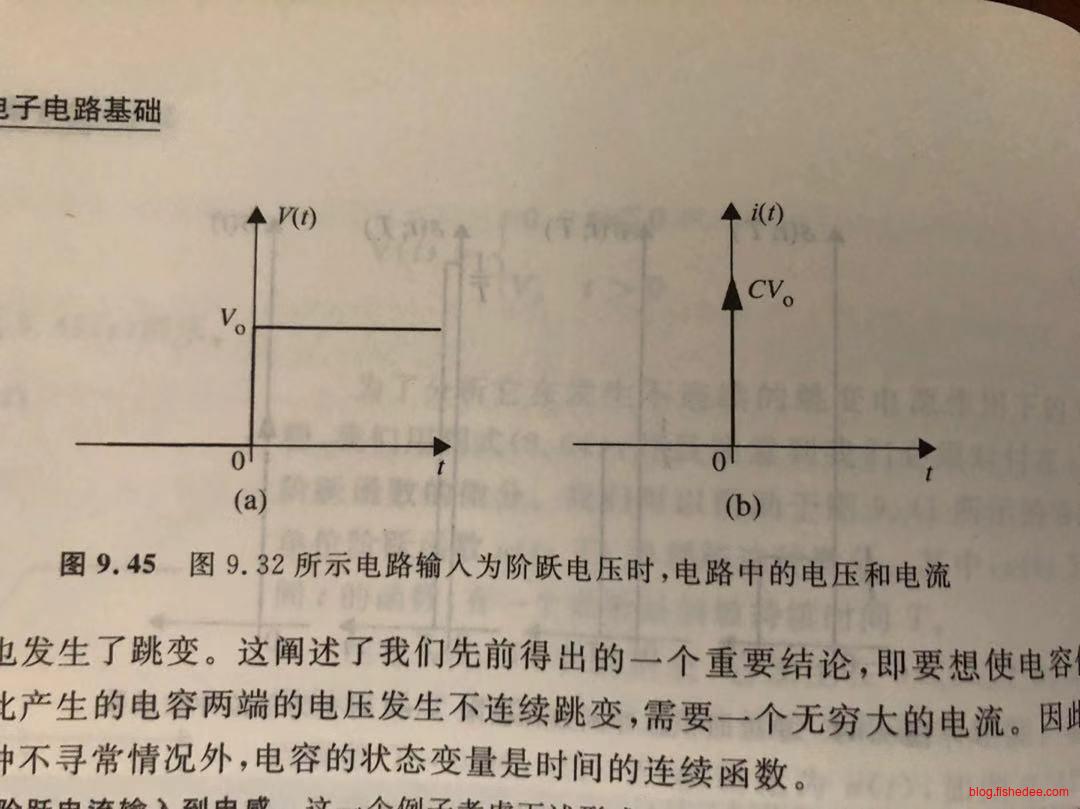
\[ V(t) = \begin{cases} 0,t\leq 0\\ V_0,t\gt 0\\ \end{cases} \]
当电压是跃阶输入,就是以上方程的时候,根据公式
\[ i(t) = C \frac {dV(t)} {dt}\\ i(t) = C V_0 \frac {du(t)}{dt} = CV_0\delta (t) \]
得到\(i(t)\)是一个冲激函数,积分值为\(CV_0\),冲激函数的特点是
\[ \delta (t) = 0 , t\neq 0\\ \int_{-\infty}^{\infty} \delta (t) dt = 1 = u(t)\\ \]
冲激函数的积分刚好就是一个跃阶函数
10.4.3 电压源驱动电感
\[ V(t) = \begin{cases} 0,t\leq 0\\ V_0,t\gt 0\\ \end{cases} \]
同理,输入是电压源时
\[ i(t) =\frac{1}{L}\int_{-\infty}^t V(t)dt\\ i(t) = \begin{cases} 0,t \leq 0\\ \frac {V_0t}{L},t\gt 0\\ \end{cases} \]
得到\(i(t)\)是一个线性函数
10.4.4 电流源驱动电感
\[ I(t) = \begin{cases} 0,t\leq 0\\ I_0,t\gt 0\\ \end{cases} \]
当电压是跃阶输入,就是以上方程的时候,根据公式
\[ v(t) = L \frac {dI(t)} {dt}\\ v(t) = L I_0 \frac {du(t)}{dt} = CI_0\delta (t) \]
得到\(v(t)\)是一个冲激函数,积分值为\(CI_0\)
10.5 冲激输入
10.5.1 电流源驱动电容
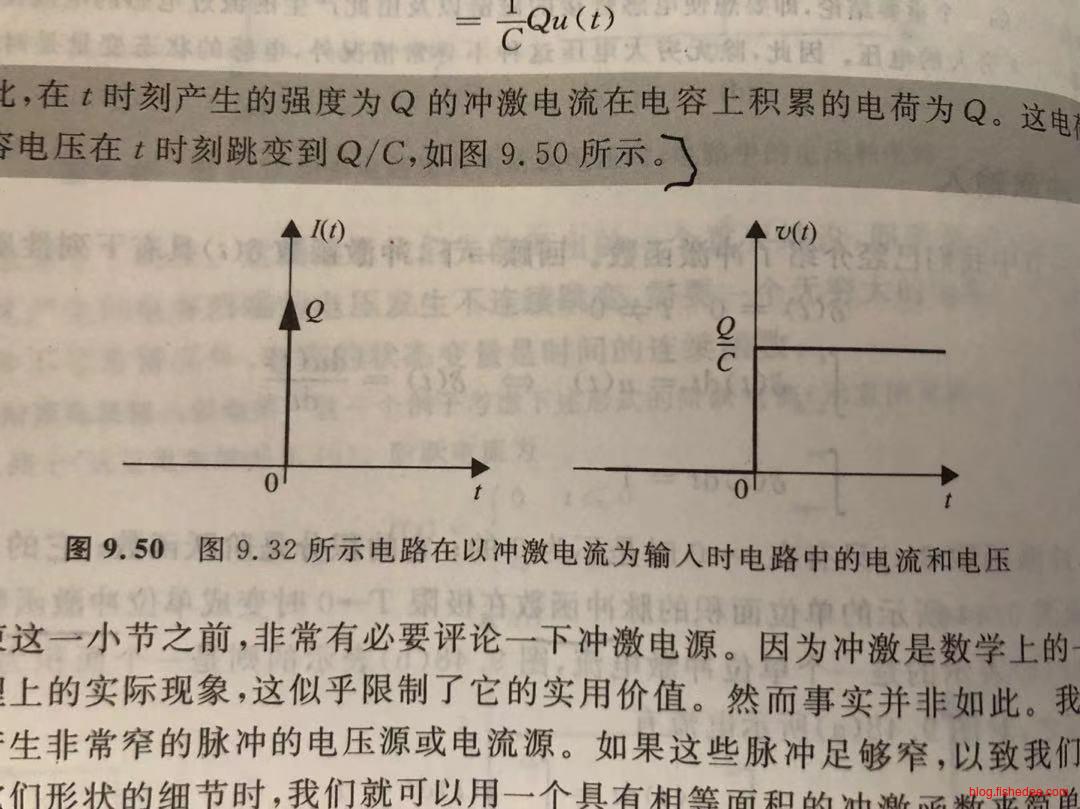
当输入电流为冲激电流,强度为Q,也就是积分为Q的电流
\[ V(t) = \frac {1} {C} \int_{-\infty}^{\infty} I(t)dt\\ = \frac {1} {C} Q \int_{-\infty}^{\infty} \delta(t) dt\\ = \frac {Q} {C} u(t) \]
得到的电压就是一个跃阶电压
10.5.2 电压源驱动电感
当输入电压为冲激电压,强度为Q,也就是积分为Q的电压
\[ i(t) = \frac {1} {L} \int_{-\infty}^{\infty} V(t)dt\\ = \frac {1} {C} Q \int_{-\infty}^{\infty} \delta(t) dt\\ = \frac {Q} {C} u(t) \]
得到的电流就是一个跃阶电压
11 线性电气网络的一阶暂态过程
11.1 RC电路
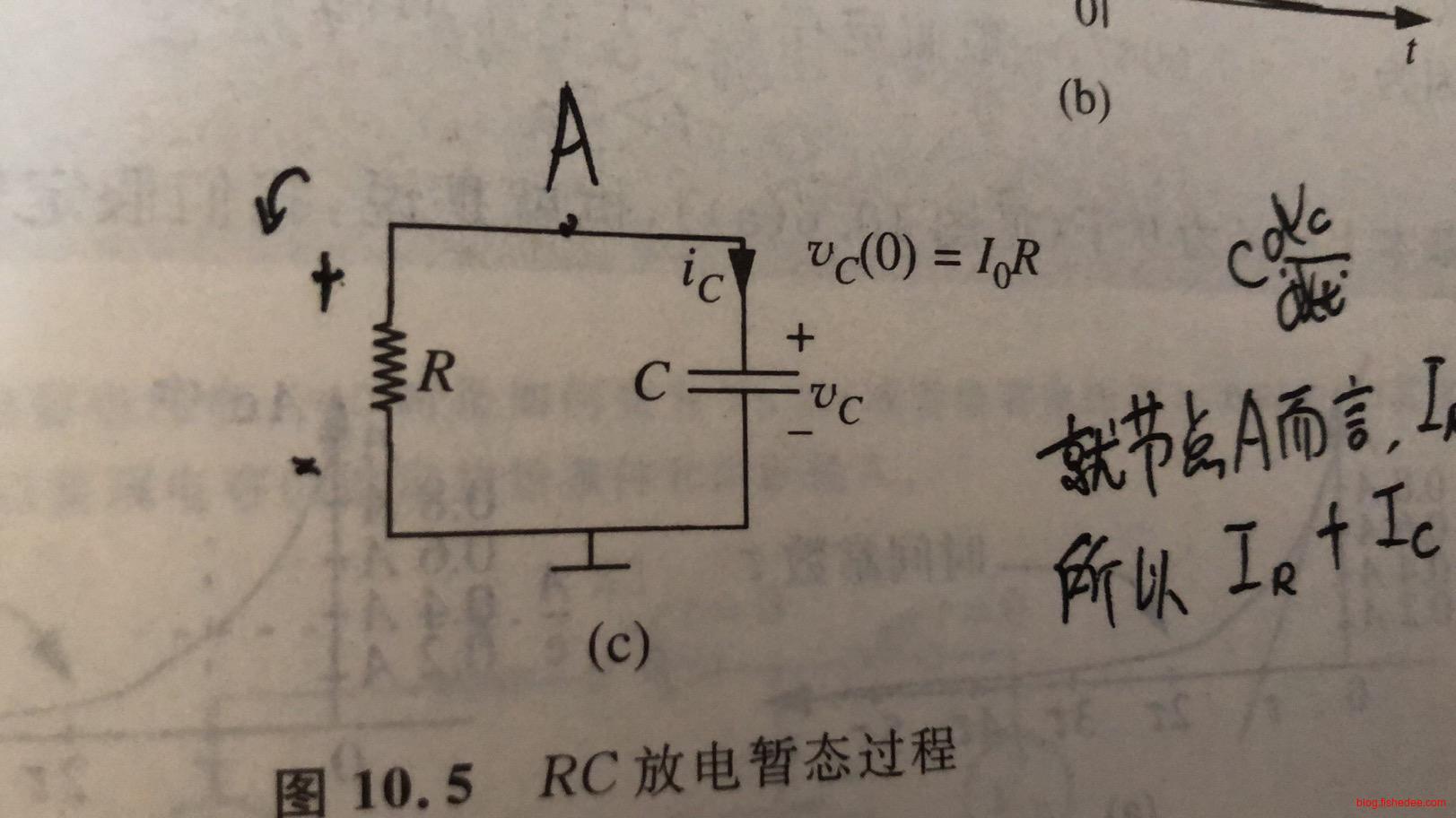
11.1.1 放电电路
这是一个电容,直接连接一个电阻,电容的初始电压非零,为\(v_C(0)\),求\(v_C(t)\),那么我们有:
\[ 0 = \frac {v_C} {R} + C \frac {dv_C} {dt} \]
这是一个齐次微分方程,它的解形式为:
\[ v_C = Ae^{st} \]
我们要求A和s的参数就可以了,代入后得到:
\[ \frac {Ae^{st}}{R} + C sA e^{st} = 0\\ \frac {1} {R}+ sC = 0\\ s = -\frac{1} {RC} \]
现在,我们求出了参数s,然后我们要求的参数A。我们可以通过初始条件来求出:
\[ v_C(0) = v_C(t=0)= Ae^{-\frac{t}{RC}}=A\\ A = v_C(0) \]
因此,我们得到结果为:
\[ v_C(t) = v_C(0)e^{-\frac{t}{RC}} \]
解齐次微分方程的步骤为,先猜测它的解形式,然后通过代入原方程,和初始条件来求出它的参数。
11.1.2 充电电路
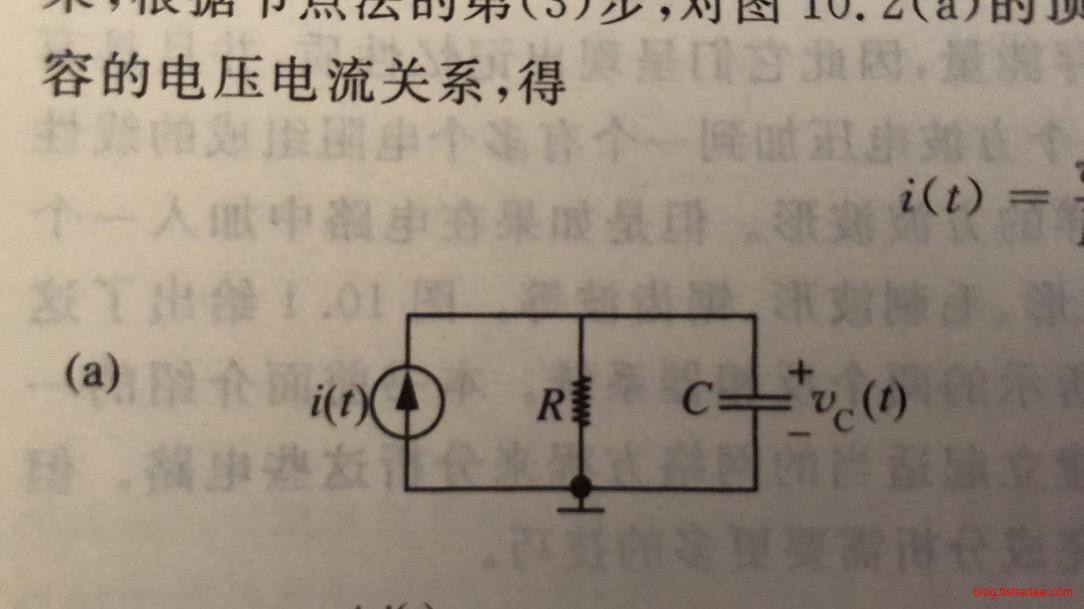
我们要求电容电压,\(I(t)\)为阶跃电流源\(I_0\),电容的初始电压为0,设定电容的电压为\(v_C\),则
\[ i(t) = \frac {v_C} {R} + C \frac {dv_C}{dt} \]
这是一个非齐次微分方程,它的解为齐次微分方程的解,和非齐次微分方程的任意解相加就可以了。
\[ 0 = \frac {v_C} {R} + C \frac {dv_C}{dt} \]
这是非齐次微分方程,对应的齐次微分方程,显然,这个解为:
\[ v_C = Ae^{-\frac{t}{RC}} \]
我们猜测非齐次微分方程的一个解为,常数K,代入得
\[ I_0 = \frac {K} {R}+ 0\\ K = I_0R \]
证明我们猜测的非齐次解的形式是正确的,我们剩下齐次微分方程的A未求得,通过\(v_C(0)=0\),可以得到
\[ Ae^{-\frac{t}{RC}}+I_0R=0\\ A+I_0R=0\\ A=-I_0R\\ \]
因此,最终的结果为:
\[ v_C = -I_0Re^{-\frac{t}{RC}}+I_0R \]
解非齐次微分方程的步骤为,先猜测它的齐次解形式,求出部分齐次解。然后再猜测它的非齐次解形式,并求出全部非齐次解,最后通过初始条件求出所有参数。方程的结果为齐次解与非齐次解的和。
11.1.3 特点
\[ v_C(t) = v_C(0)e^{-\frac{t}{RC}} \]
从放电电路解可以看出,当\(t=RC\)时,结果固定为\(v_C(0)e^{-1}\),这与R与C的具体值无关。所以,我们将RC乘积为衰减的时间常数,而我们一般将5倍的RC时间常数看成是衰减到0的时间。
11.2 RL电路
11.2.1 放电电路
RL放电电路,和RC电路是类似的,假设电感原有电流为\(i_L(0)\),与它串联的电阻后,它的电流变化为:
\[ L\frac{di_L}{dt}+i_LR=0 \]
这是一个齐次方程,最终解为:
\[ i_L(t) = i_L(0)e^{\frac{-t}{L/R}} \]
11.2.2 充电电路
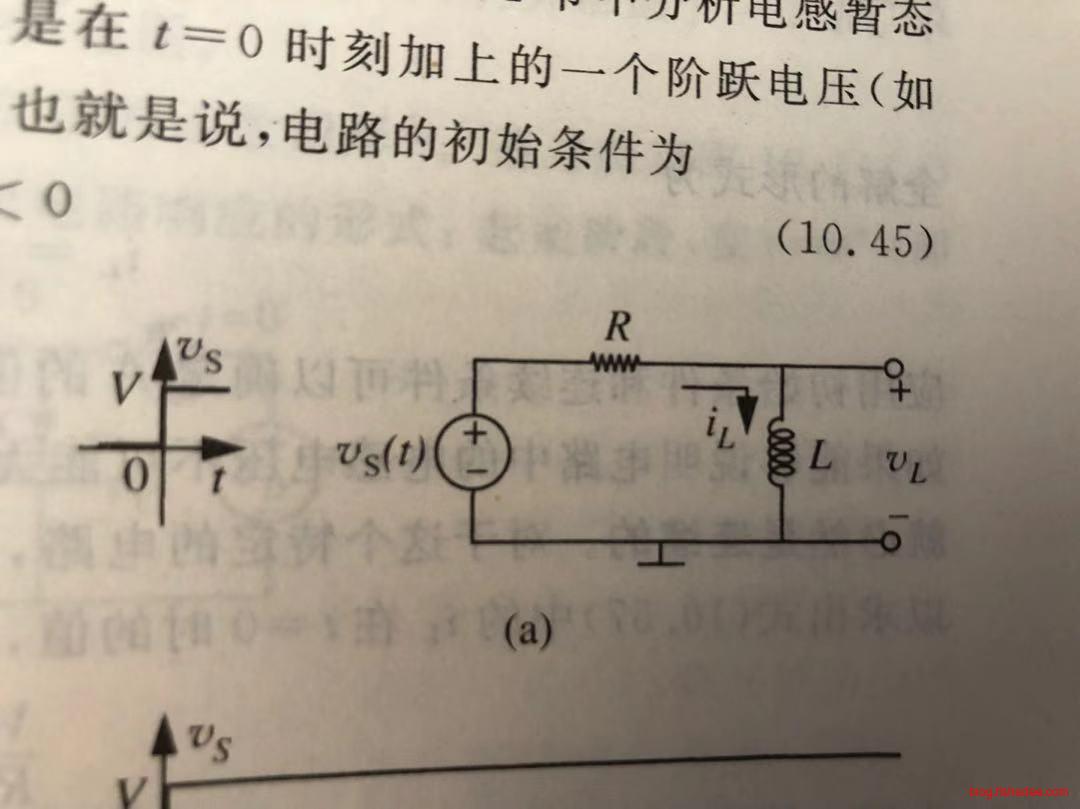
这是一个阶跃电压,加入到初始电流为0的电感上,它的电流变化为:
\[ -v_S+L\frac{di_L}{dt}+i_LR=0 \]
这是一个非齐次方程,最终解为:
\[ i_L(t) = -\frac{V}{R}e^{\frac{-t}{L/R}}+\frac{V}{R} \]
11.2.3 特点
\[ i_L(t) = i_L(0)e^{\frac{-t}{L/R}} \]
解的形式和RC电路非常相似,仅仅是将RC时间常数,改为L/R时间常数而已。
11.3 状态变量
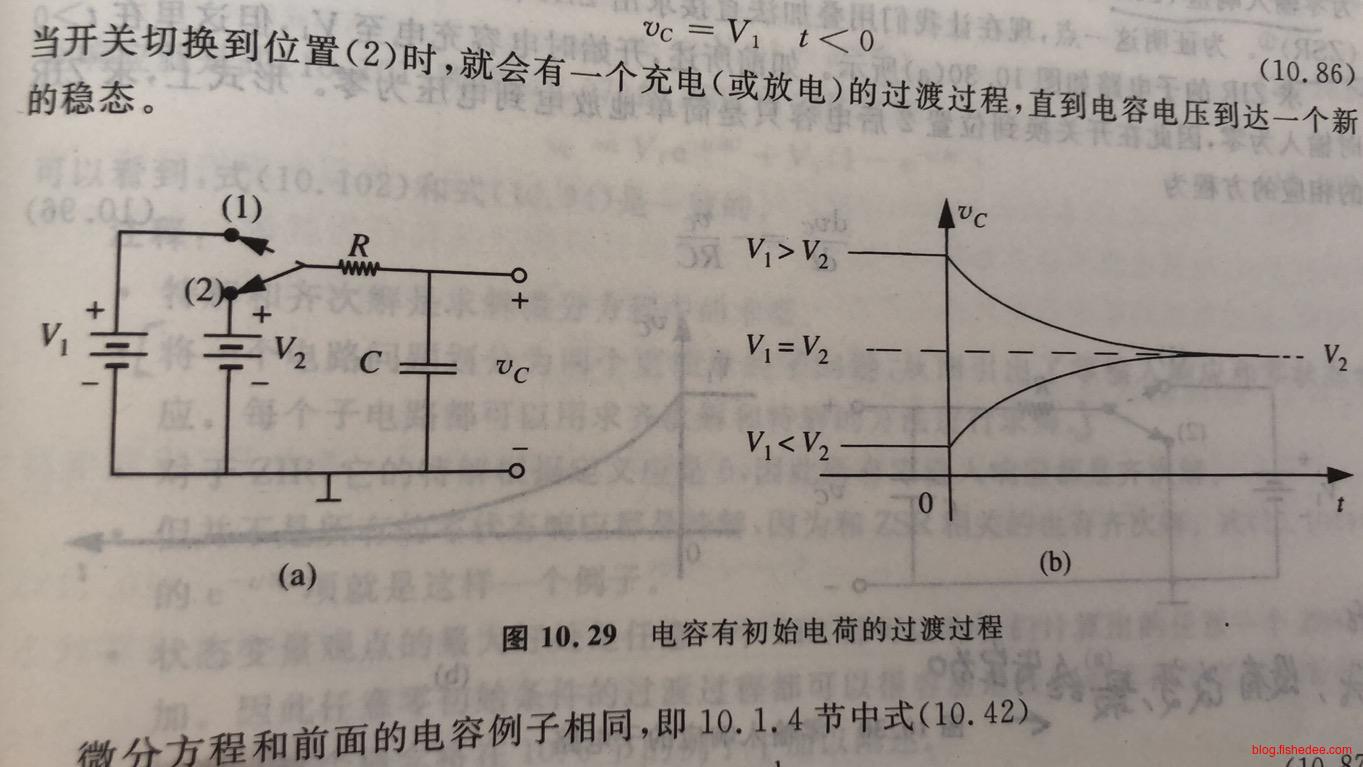
我们之前的讨论,要么是初始电压不为0的放电电路,要么是初始电压为0的充电电路。那么,如果是初始电压不为0的充电电路呢。从微分方程中,我们可以最终推导出来,结果是:
\[ v_C = -V_2e^{-\frac{t}{RC}}+V_2+V_1e^{-\frac{t}{RC}}\\ = V_2(1-e^{-\frac{t}{RC}})+V_1e^{-\frac{t}{RC}} \]
这正好是,初始电压不为0的放电电路的解,与初始电压为0的充电电路的解,的和。因此,我们不加证明地,指出,对于初始状态不为0,初始输入也不为0的RC或者RL电路,它的方程为以下两部分的解:
- ZIR零输入相应,初始状态不为0,初始输入为0的电路,也就是放电电路。对于阶跃输入,其方程总是为\(v_c(1-e^{-\frac{t}{RC}})\)的形式。
- ZSR零状态相应,初始状态为0,初始输入不为0的电路,也就是充电电路。对于阶跃输入,其方程总是为\(v_ce^{-\frac{t}{RC}}\)的形式。
这个定理大大地方便了,我们对RC或者RL电路的解。
11.4 其他输入
我们之前讨论的都是阶跃输入下的结果,那么RC或者RL电路不是阶跃输入如何处理。
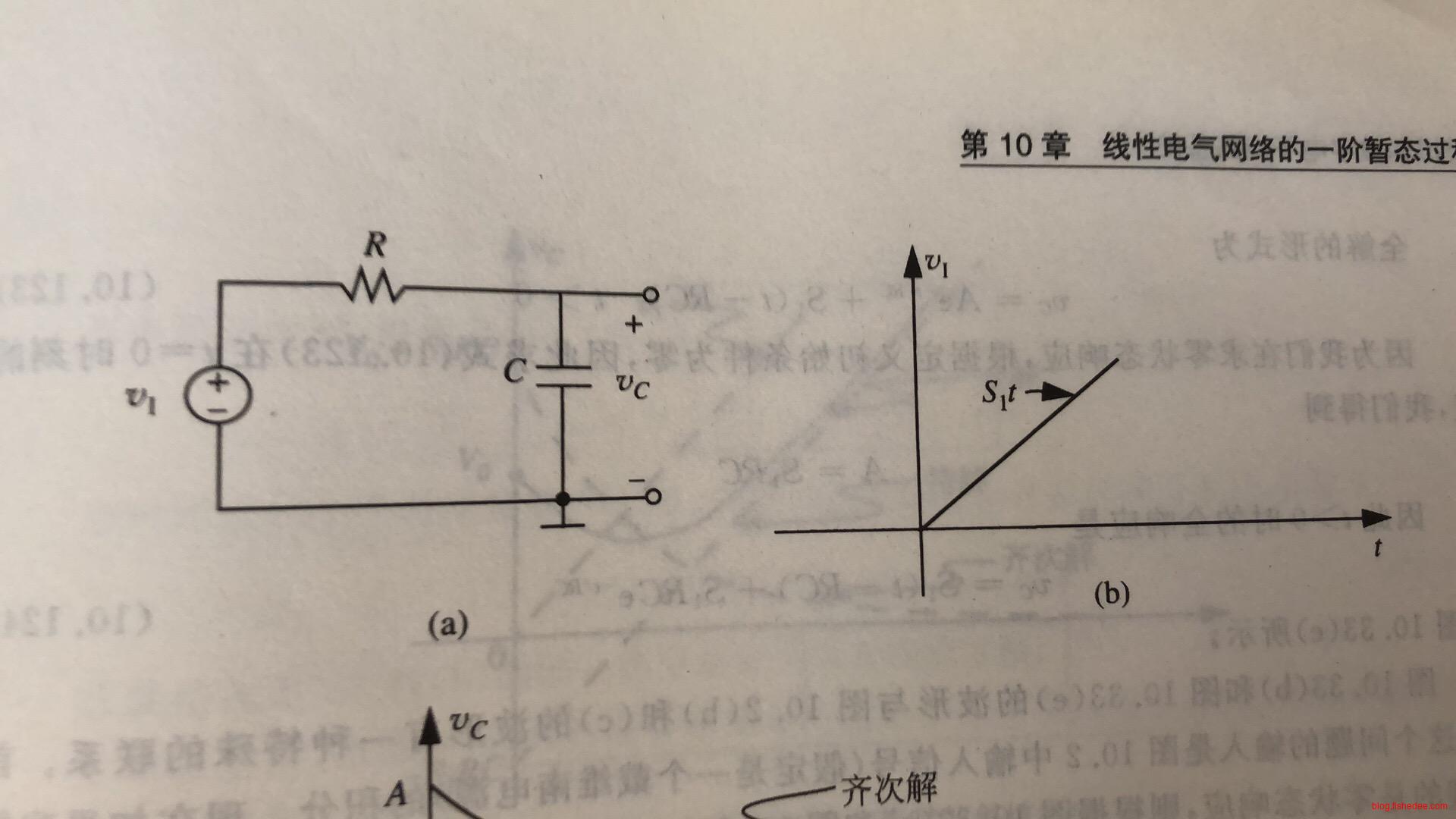
11.4.1 线性输入
对于输入是一个线性电路的时候,我们依然列出方程:
\[ v_{IN} = RC \frac {dv_C} {dt} + v_C\\ v_{IN} = S_1t\\ 得到:S_1t=RC \frac {dv_C} {dt} + v_C\\ \]
这又是一个非齐次微分方程,齐次方程解显然为:
\[ v_C = Ae^{\frac {-t}{RC}} \]
猜测非齐次方程的特解为:\(v_C=K_2t\),代入得到
\[ S_1t=RCK_2+K_2t \]
无法求得自由的\(K_2\)表达式,因此在此猜测非齐次方程的特解为:\(v_C=K_2t+K_3\),代入得到
\[ S_1t=RCK_2+K_2t+K_3\\ 因此K_2=S_1\\ k_3=-S_1RC\\ \]
求得当前总的解为:
\[ v_C =Ae^{\frac {-t}{RC}}+S_1t-S_1RC \]
代入初始条件\(v_C(0)=0\),得到
\[ Ae^{\frac {-t=0}{RC}}+S_1t-S_1RC =0\\ A=S_1RC \]
因此,最终结果为:
\[ v_C =S_1RCe^{\frac {-t}{RC}}+S_1t-S_1RC \]
这个解相当有意思,它的输入是线性电压,刚好是阶跃电压的积分。那么,阶跃电压下的响应为\(v_C=S(1-e^{\frac {-t}{RC}})\),其中S为阶跃的固定电压。有意思的地方是,阶跃电压下的响应的积分,刚好就是线性电压下的响应!这是因为在线性系统中,线性算子可以交换使用,先积分再求响应,或者先求响应后积分,是一样的结果!
另外,如果电容的初始状态不为0,是某个电压\(V_0\)。那么结果就是ZIR+ZSR,就是:
\[ v_C =V_0e^{\frac{-t}{RC}}+S_1RCe^{\frac {-t}{RC}}+S_1t-S_1RC \]
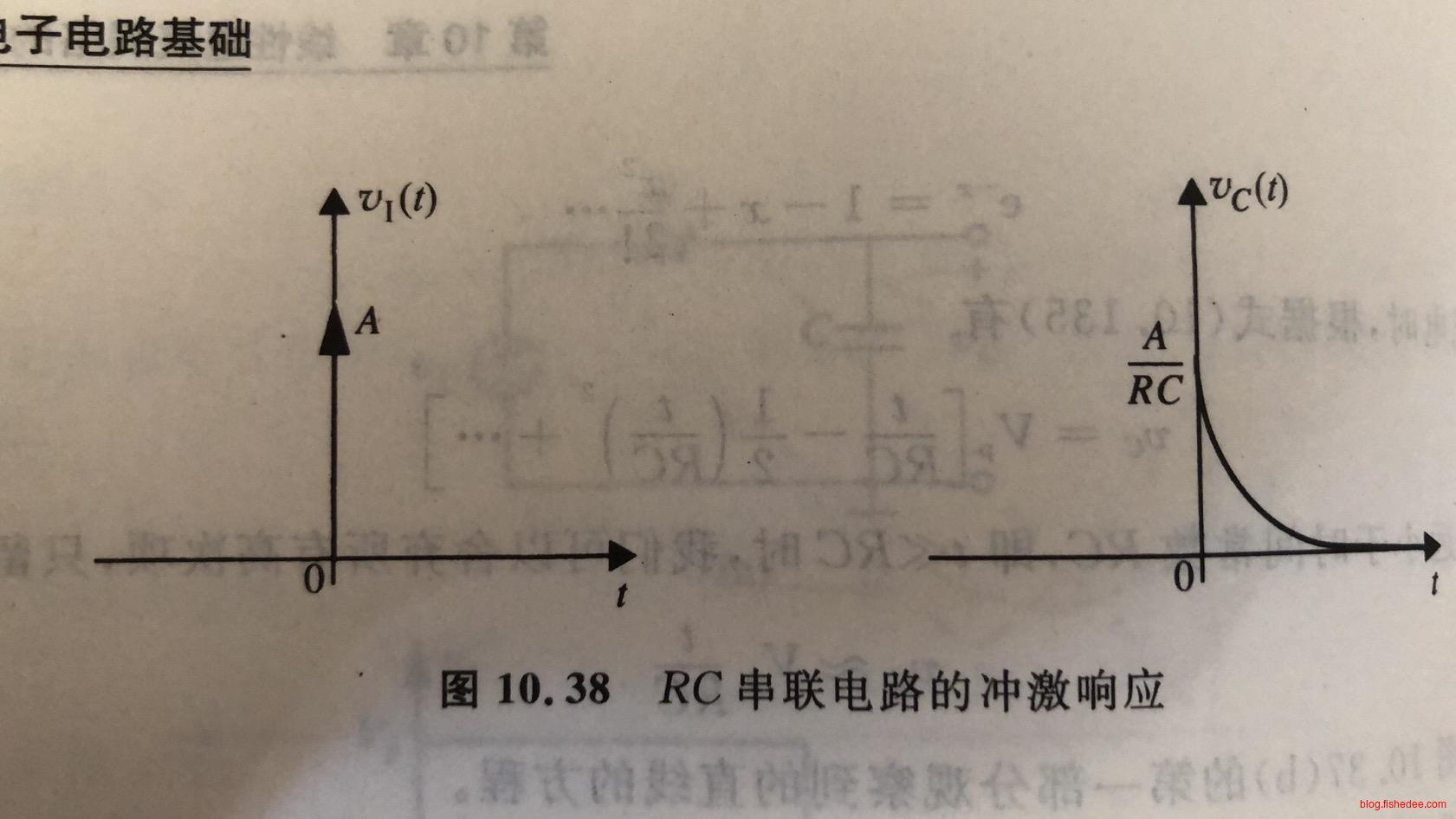
11.4.2 冲激输入
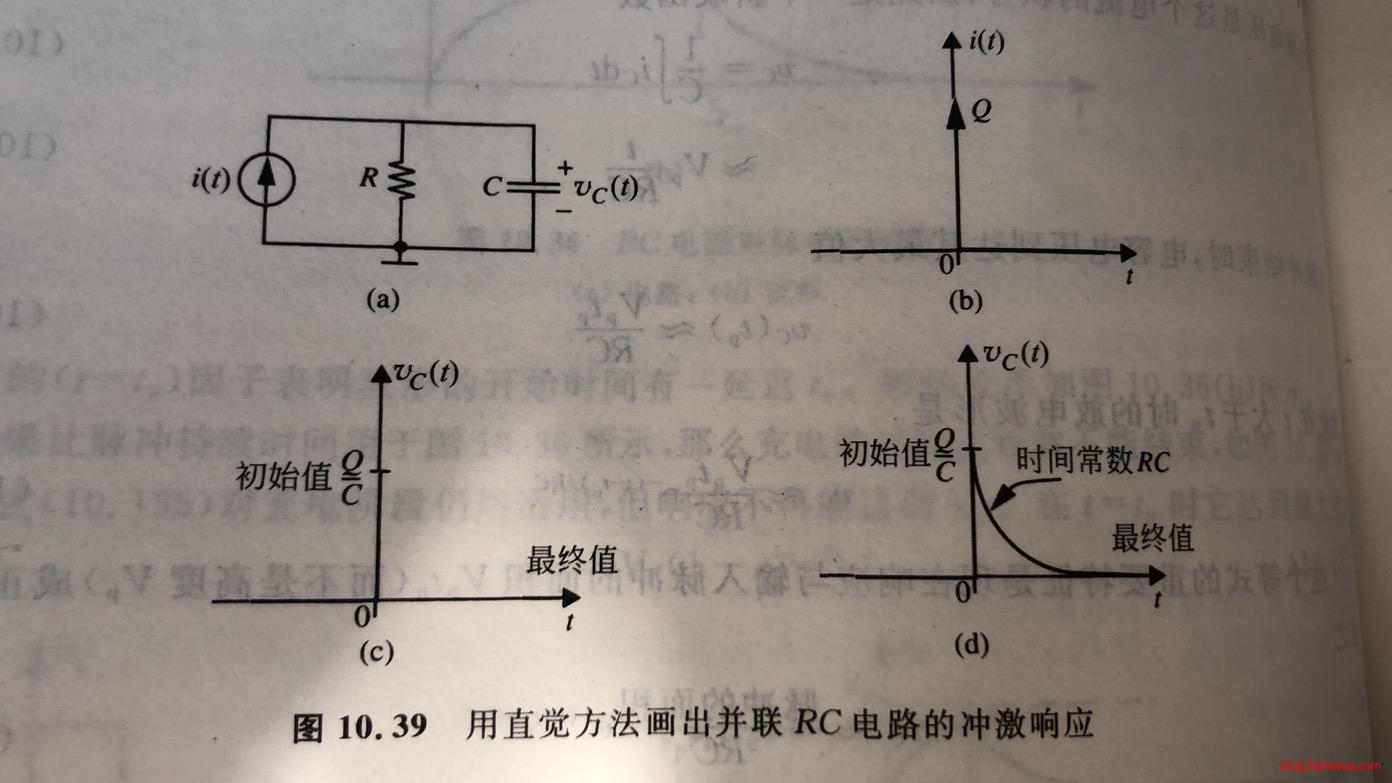
我们不加证明地指出,当冲激电压源加到RC电路中时,相当于初始电压为\(\frac{A}{RC}\)的电容放电
当冲激电流源加到RC电路中时,相当于初始电压为\(\frac{Q}{C}\)的电容放电
11.4.3 正弦输入
对于正弦输入下的RL电路,也是一样的套路,列方程,然后求微分方程就可以了
\[ v_I=i_LR+L\frac {di_L} {dt}\\ v_I=Vsin(\omega t)\\ Vsin(\omega t)=i_LR+L\frac {di_L} {dt} \]
这是一个非齐次微分方程,齐次解为:\(i_L=Ae^{\frac{-t}{L/R}}\)。
我们猜测非齐次的解为:\(i_L=Ksin(\omega t)\),代入后发现不行。
然后猜测非齐次的解为:\(i_L=K_1sin(\omega t)+K_2cos(\omega t)\),代入后得到
\[ Vsin(\omega t) = K_1Rsin(\omega t)+K_2Rcos(\omega t) + L\omega K_1 cos(\omega t)-L\omega K_2 sin(\omega t)\\ V=K_1R-K_2L\omega\\ 0=K_1L\omega +K_2R\\ \]
就这样我们能得到\(K_1\)和\(K_2\),然后加入齐次解,和初始条件,我们得到最终的方程为:
\[ i_L=Ae^{\frac{-t}{L/R}}+V\frac{R}{R^2+\omega ^2L^2}sin(\omega t)-V\frac {\omega L}{R^2+\omega^2 L^2}cos(\omega t)\\ 其中A=\frac {V\omega L} {R^2+\omega^2 L^2} \]
从方程中可以看出,电流是一个衰减和正弦的结合,当t足够大时,第一项就消失了,剩下的就是正弦。当频率较大时,主要是第二项做起作用,电流接近为\(\frac {V}{R}\)。当频率较大时,主要是第三项在起作用,这个时候电流接近为0。
11.5 MOSFET元件
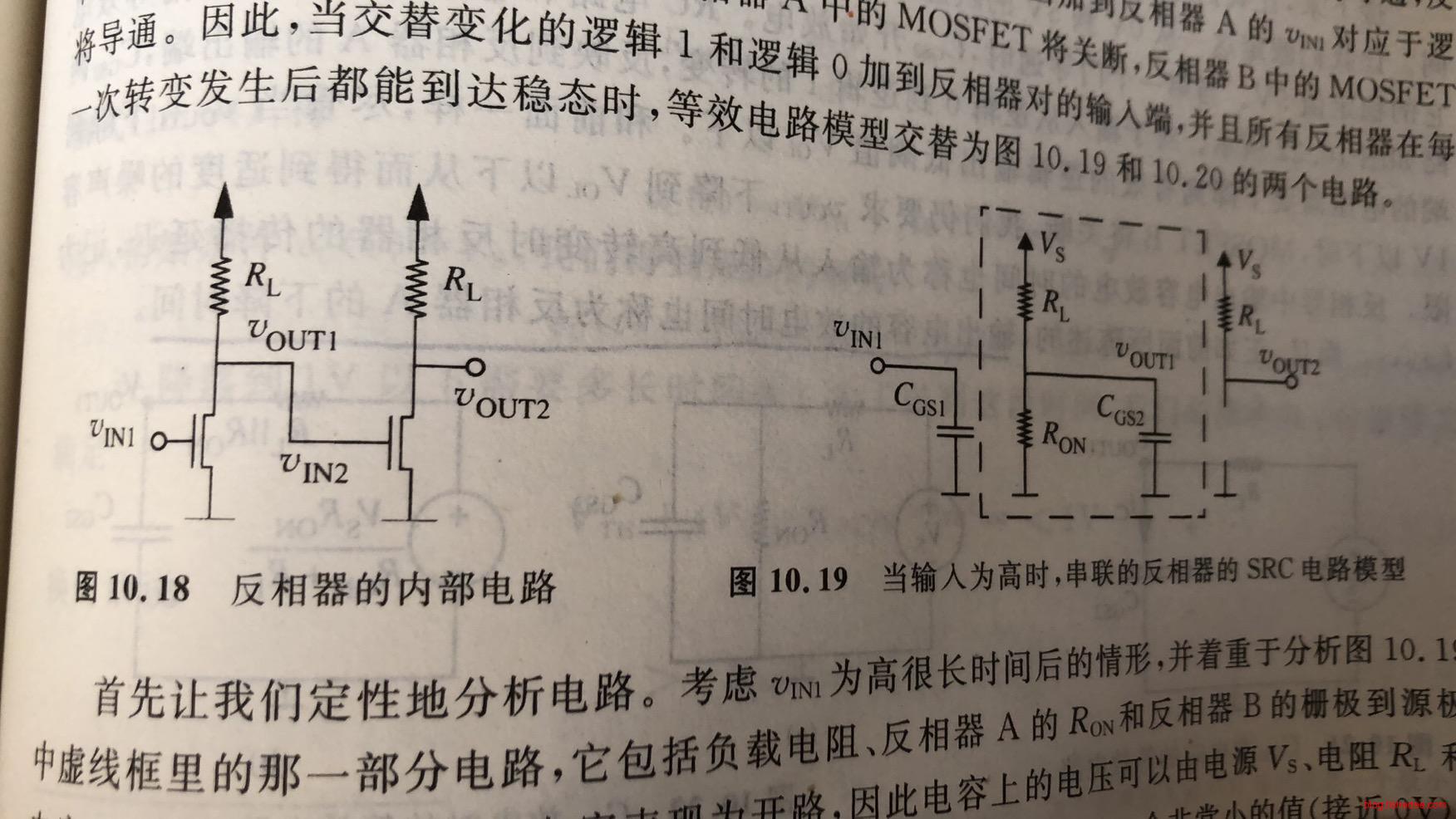
11.5.1 SRC模型
我们之前一直认为MOSFET元件的输出是即时的,但这样是不符合实际的。MOSFET元件的栅极与源极之间包含了一个实际的电容\(C_{GS}\),这个电容会影响输出的电平转变。这个就是从MOSFET的SR模型改进过来的SRC模型。
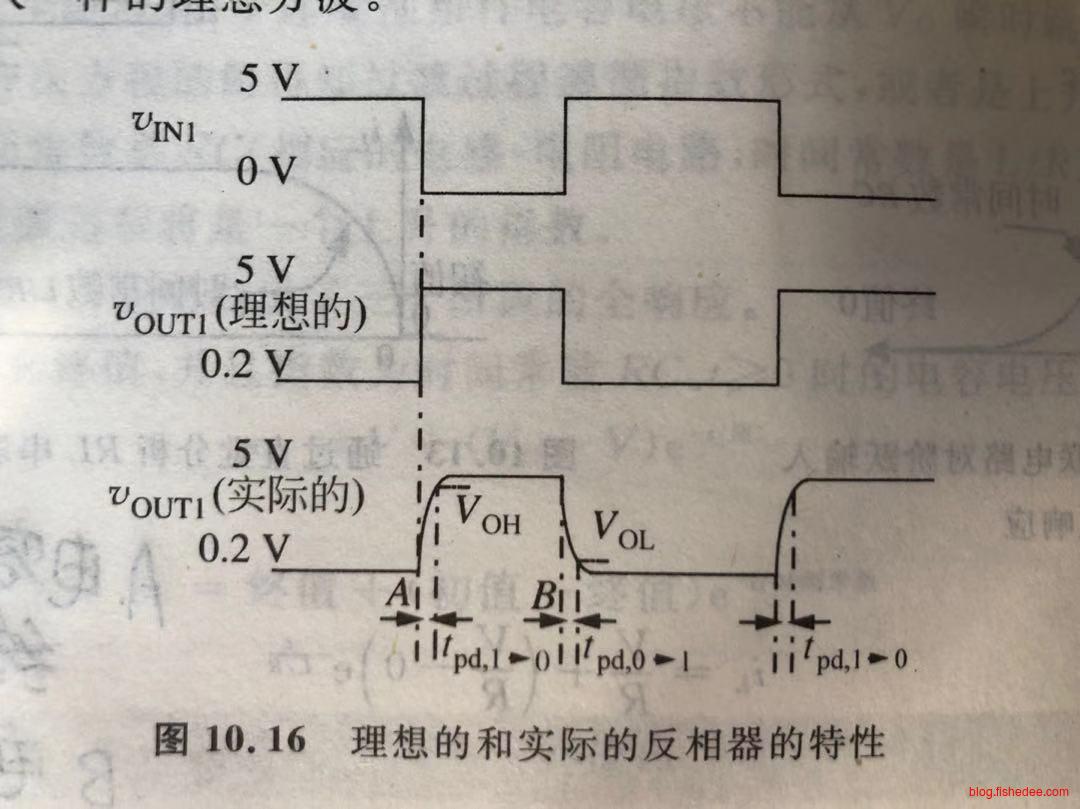
11.5.2 传播延迟
这是反相器实际的输出图形,我们可以看出有两个延迟
- \(t_{pd,1\to 0}\),当输入端发生从高到低的瞬时跃迁信号后,输出到达有效输出电平的时间间隔。对于反相器来说,这个时间是输出从低电平上升\(V_{OH}\)的时间。
- \(t_{pd,0\to 1}\),当输入端发生从低到高的瞬时跃迁信号后,输出到达有效输出电平的时间间隔。对于反相器来说,这个时间是输出从高电平下降升\(V_{OL}\)的时间。 传播延迟
传播延迟就是
\[ t_{pd}=\max(t_{pd,1\to 0},t_{pd,0\to 1}) \]
另外,对于一个包含多个门元件的电路来说,该电路的传播延迟是它的每一级门元件的传播延迟之和。这跟上升时间和下降时间是不同的,上升时间和下降时间,仅仅代表最后一层输出级门元件的速度。
最后,我们从SRC模型中可以看出,定义一个门元件的\(t_{pd}\),不仅与自身有关,还有跟后面接入的元件的\(v_{GS2}\)有关。一般来说,我们定义为驱动一个典型负载的时间——四个最小尺寸的反相器。
11.5.3 下降时间
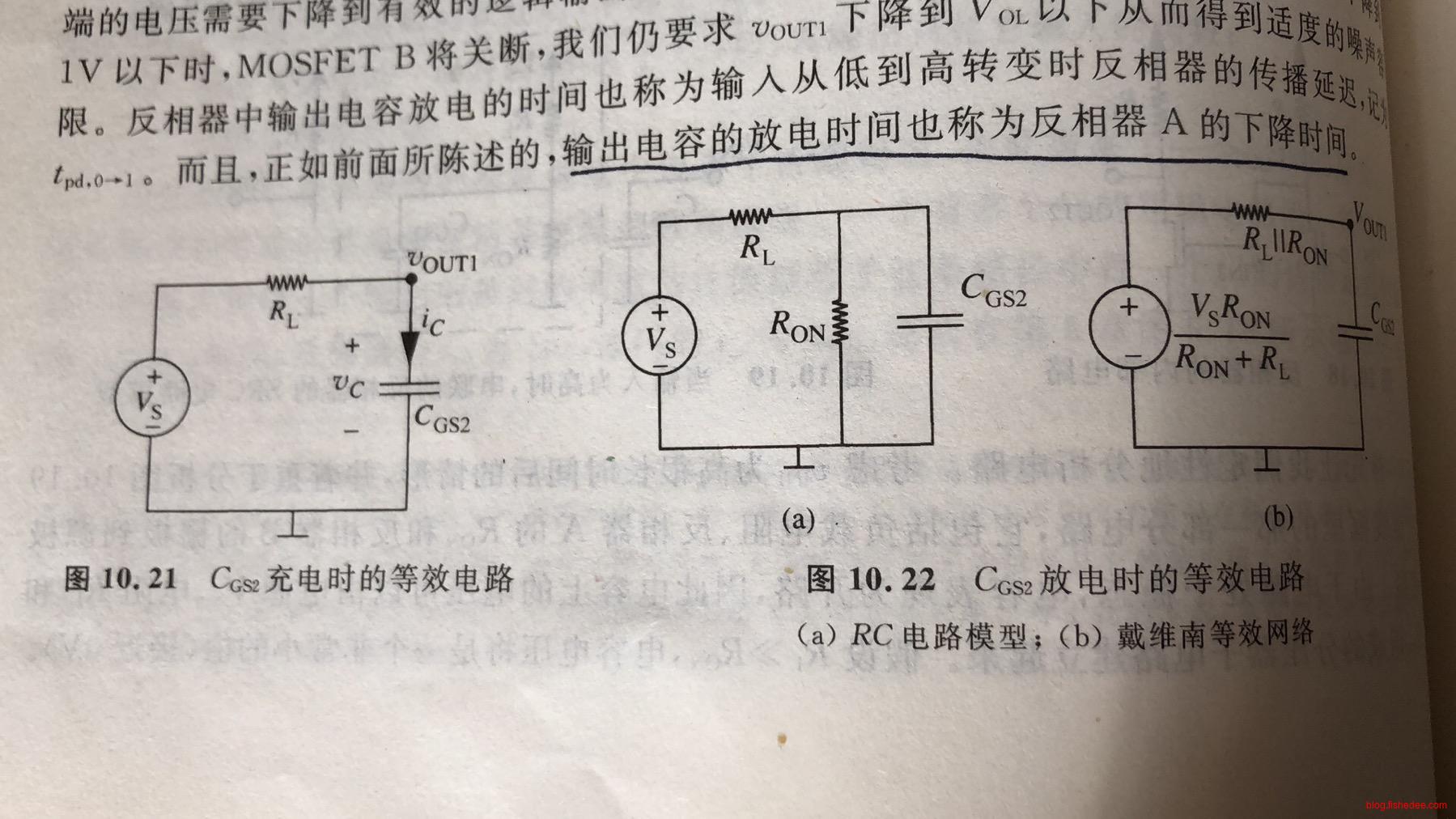
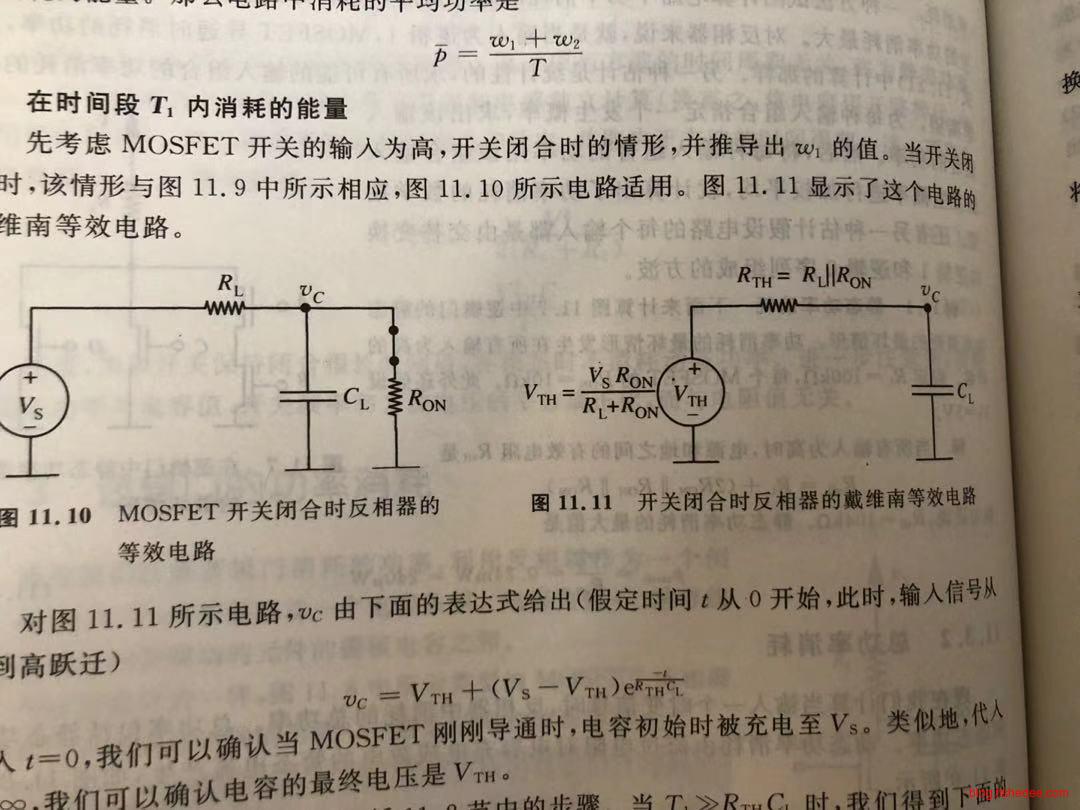
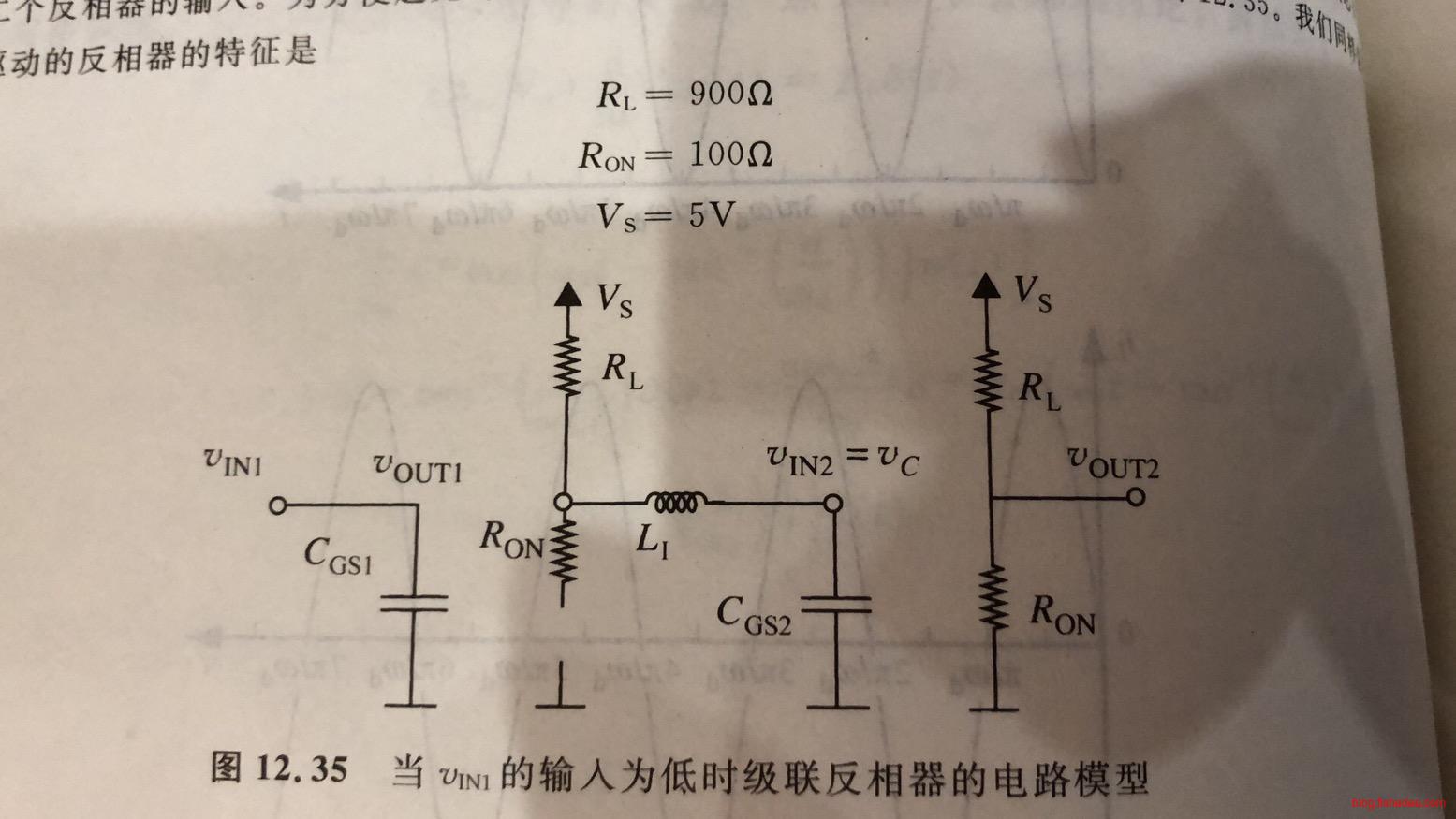
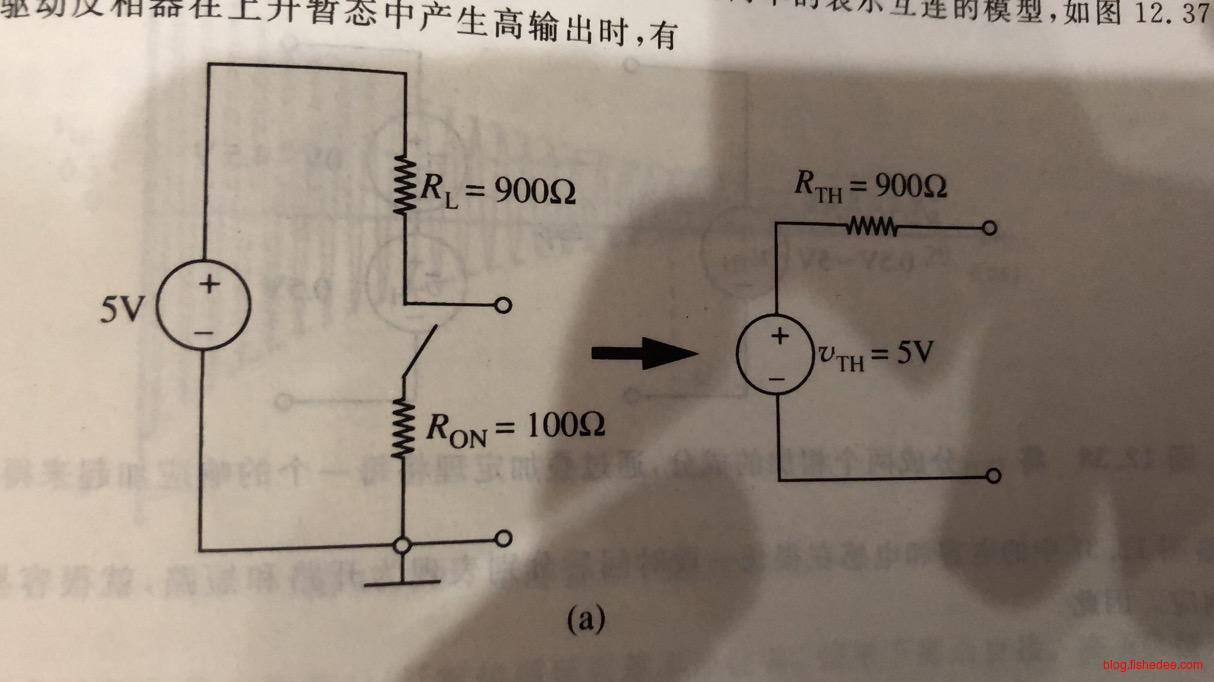
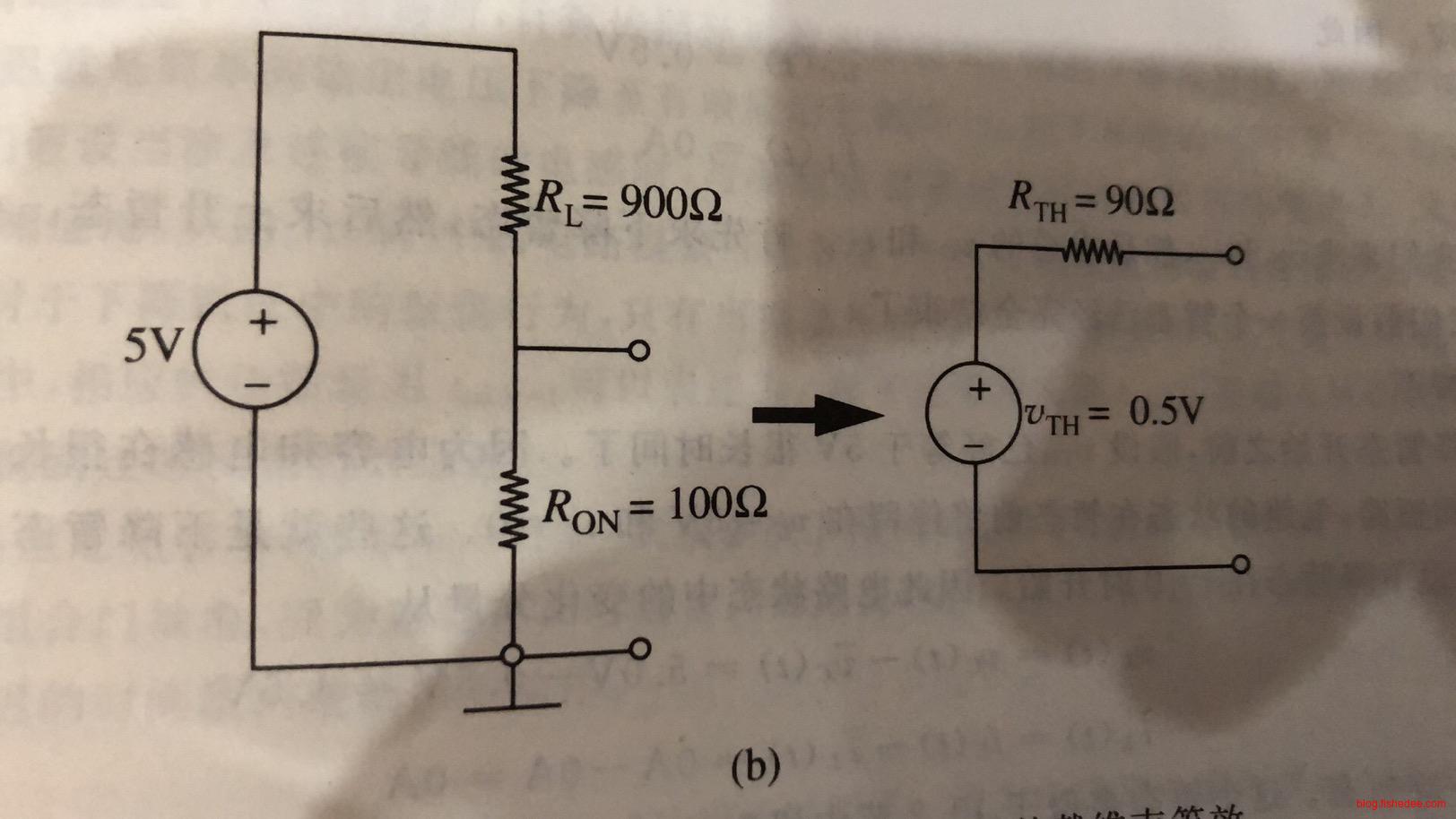
反相器的\(t_{pd,0 \to 1}\),也就是下降时间。电容器从最开始的\(V_s\)下降到\(V_{OL}\)的电路。也就是,从左边的电路,转换到右边的电路。那么,电容的初始状态为:
\[ v_C(0) = V_S \]
电容的初始输入为:
\[ V_{TH} = \frac {V_sR_{ON}} {R_{ON}+R_L}\\ \]
电路的等效电阻为:
\[ R_{TH} = R_L||R_{ON} \]
因此,电容的电压方程为:
\[ v_C=V_se^{\frac {-t}{R_{TH}C_{GS2}}}+V_{TH}(1-e^{\frac {-t}{R_{TH}C_{GS2}}}) \]
这个时间可以估计为\(R_{TH}C_{GS2}\)
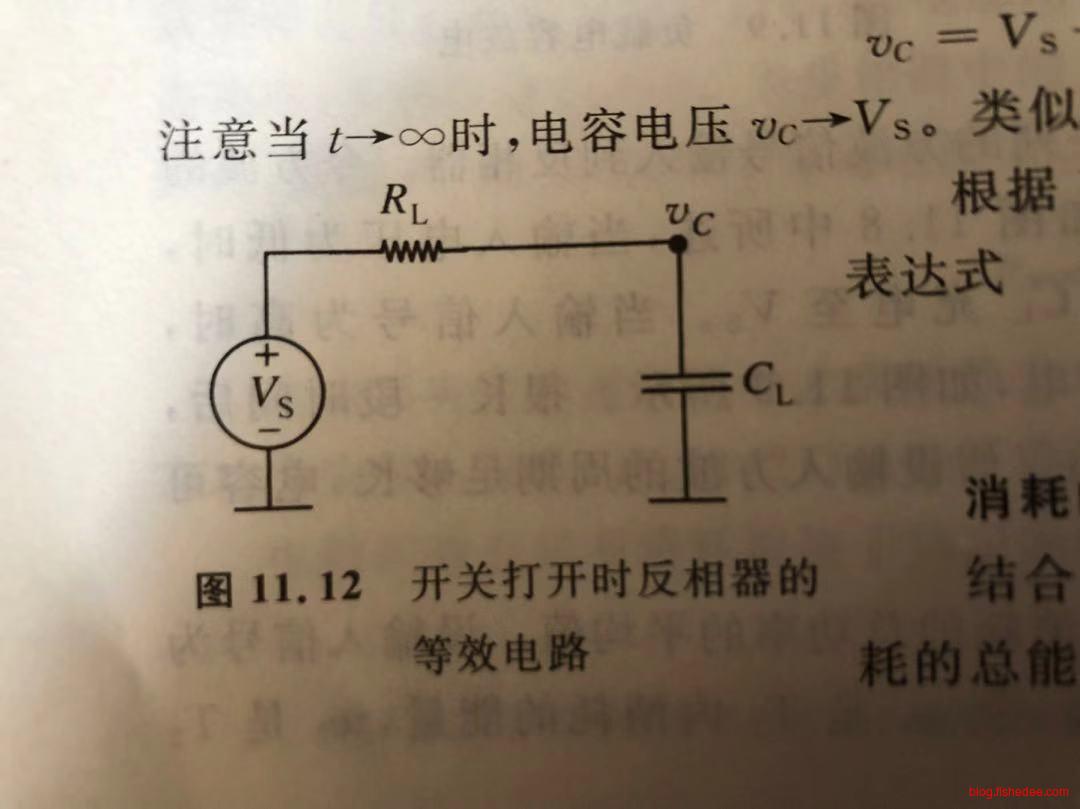
11.5.4 上升时间
反相器的\(t_{pd,1 \to 0}\),也就是上升时间。电容器从最开始的\(V_{TH}\)上升到\(V_{OH}\)的电路。也就是,从右边的电路,转换到左边的电路。那么,电容的初始状态为:
\[ V_{TH} = \frac {V_sR_{ON}} {R_{ON}+R_L}\\ \]
电容的初始输入为\(V_s\),电阻为\(R_L\)。
因此,电容的电压方程为:
\[ v_C=V_{TH}e^{\frac {-t}{R_{L}C_{GS2}}}+V_{s}(1-e^{\frac {-t}{R_{L}C_{GS2}}}) \]
这个时间可以估计为\(R_{L}C_{GS2}\)
11.5.5 总结
从时间估计中可以看出,上升时间一般是大于下降时间的,因为\(R_{L}C_{GS2} \gt R_{TH}C_{GS2}\),量级大概是1.5ns大于0.2ns。
11.6 动态存储元件
11.6.1 电容存储
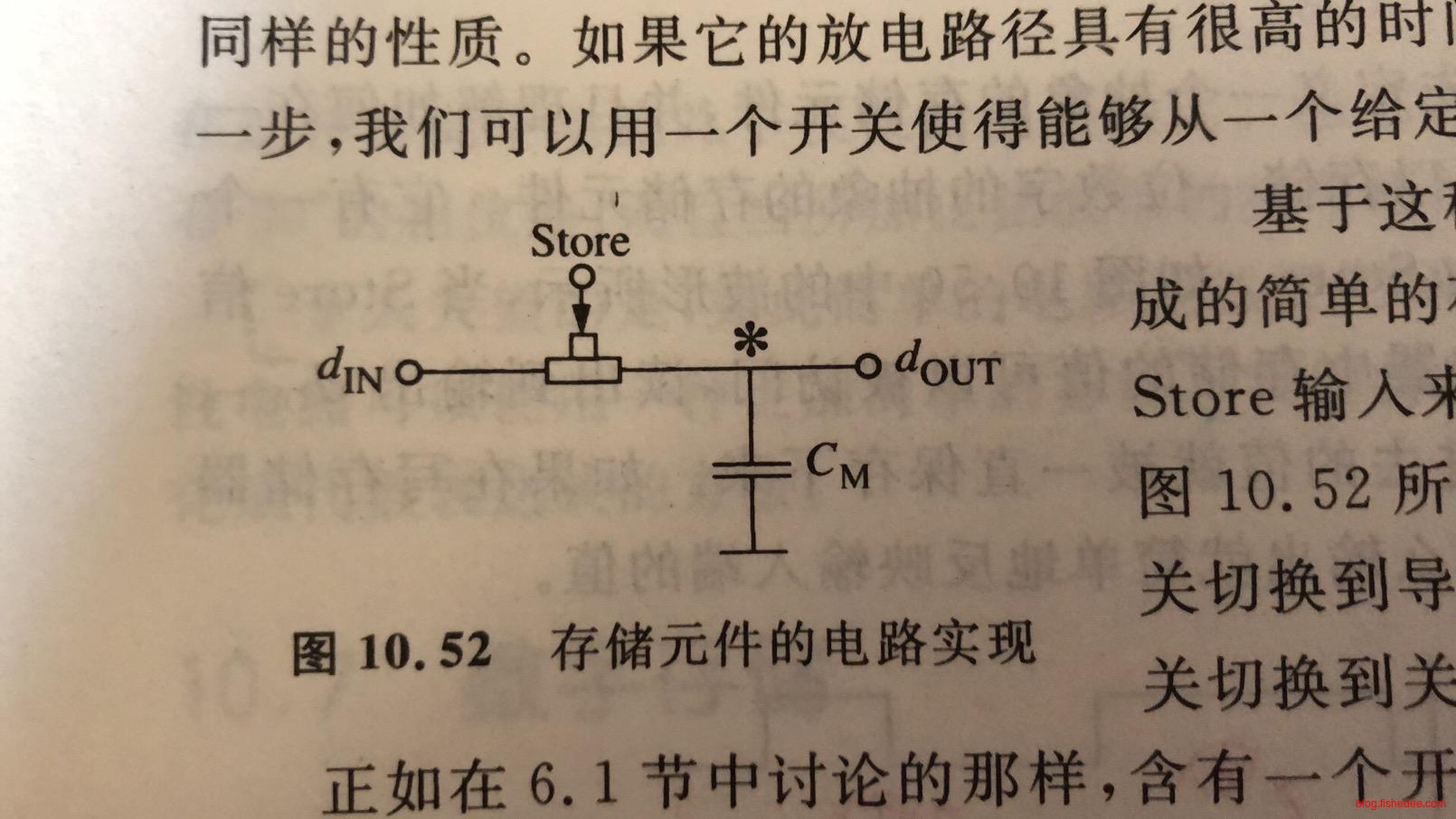
实现存储元件的简单实现,就是用一个电容来保存电平状态。当Store信号来了的时候,就直接对电容进行操作就可以了。
11.6.2 信号可重构
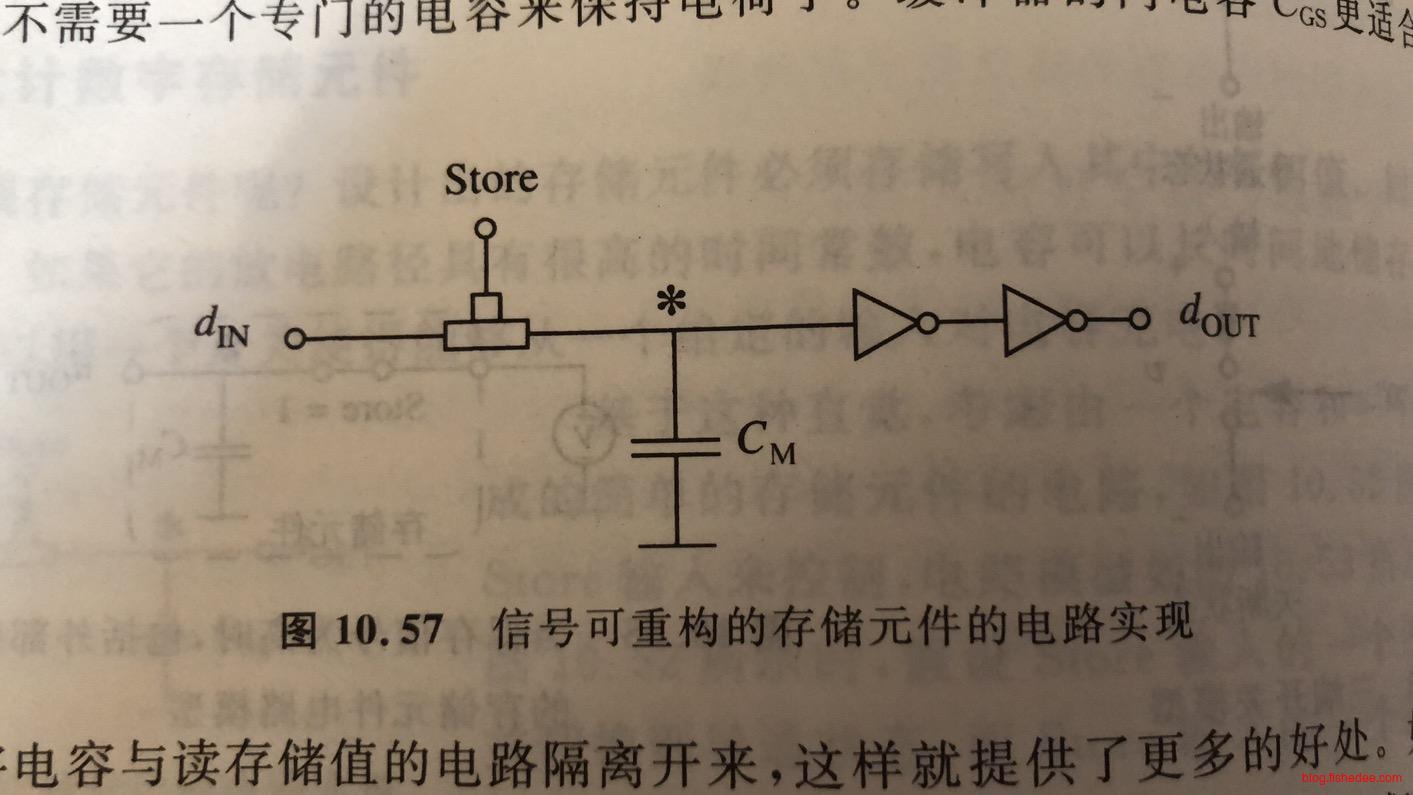
但这样做的问题是,当外部负载取到了高电平的时候,电容容易丢失电荷,甚至直到零的电平。而且,另外一个问题是,输入的电平是\(V_{IH}\)的时候,电容无法输出\(V_{OH}\)的电平,不满足静态原则。
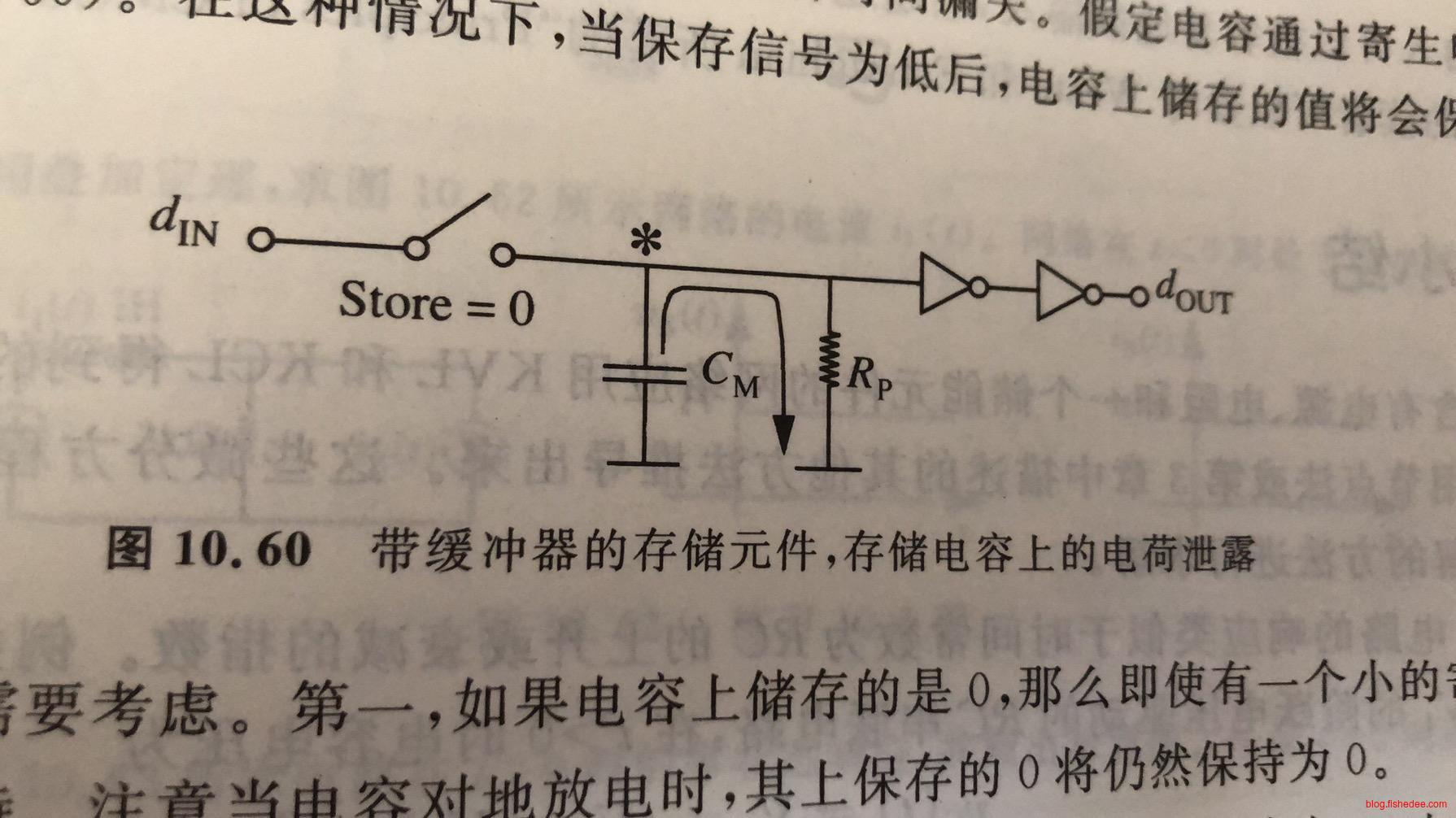
解决方法是,加入两个反相器,因为MOSFET的栅极不会通过电流,所以不用担心电荷丢失,而且输出肯定也能满足静态原则。
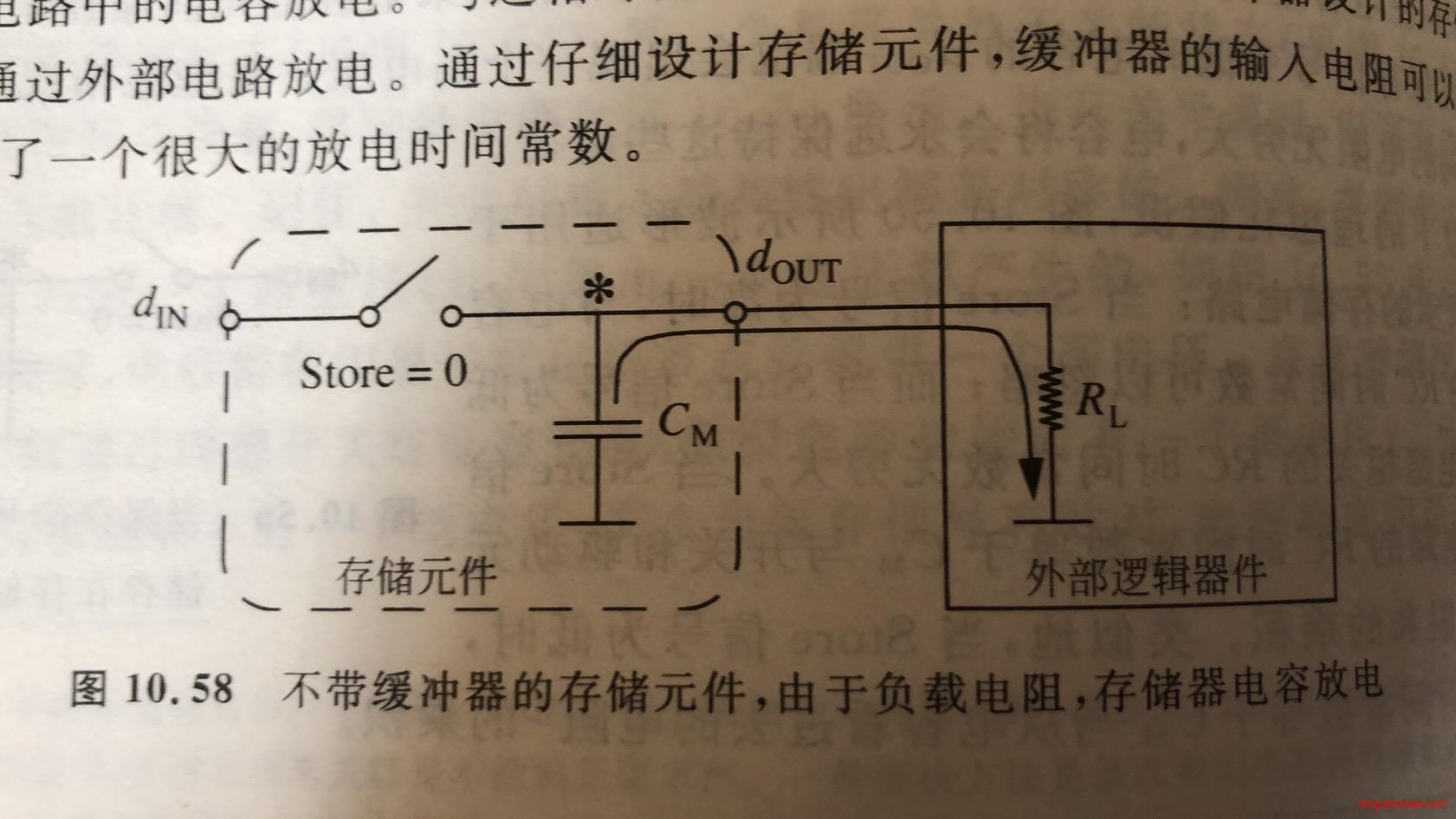
11.6.3 寄生电阻
即使加入缓冲器,总是会有寄生电阻的出现,当然,这个电阻的阻值很大。它会用比较长的时间来损耗电容上的电荷。这个时候,电容就不能有效地输出高电平了。所以,这种电路仍然需要定时刷新(0.3ms量级)来保持电容上的高电荷。
12 数字电路的能量和功率
12.1 RC电路的功率
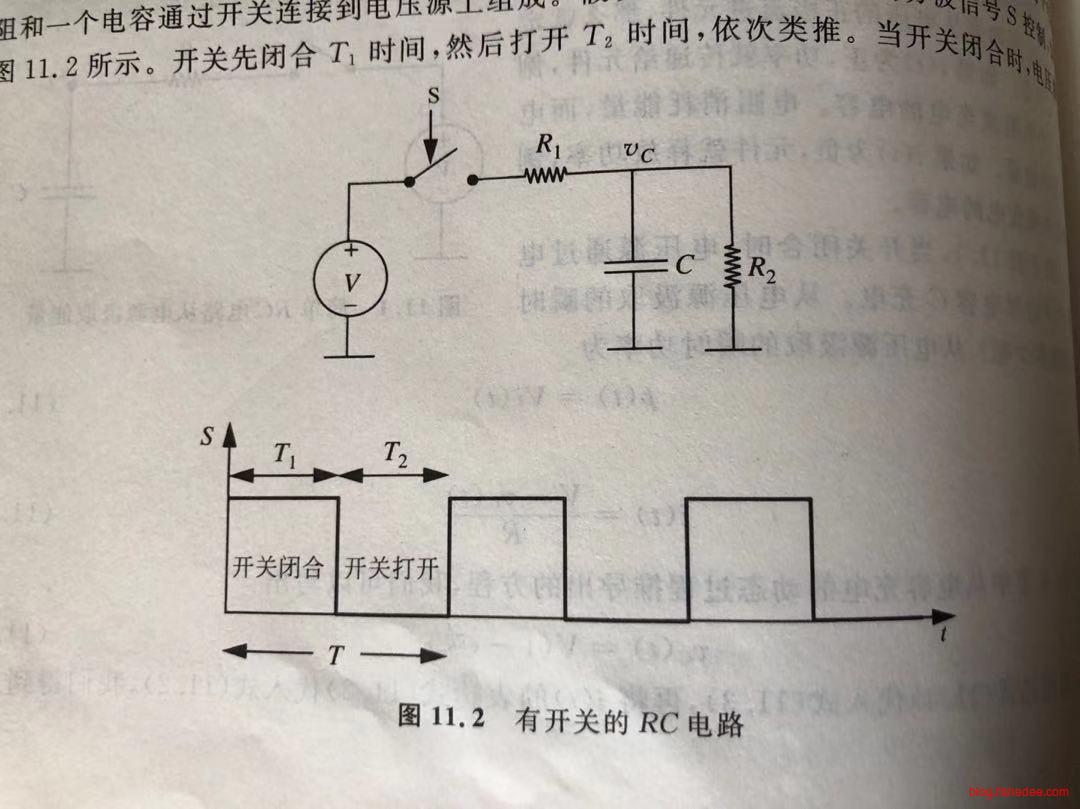
计算上述的RC电路在下面的方波信号控制的开关下的功率。严格的来说,我们只需要计算一个周期内的功率就可以了。当然,每个时间段的时间都足够长,电容都到达稳态。
12.1.1 T1阶段
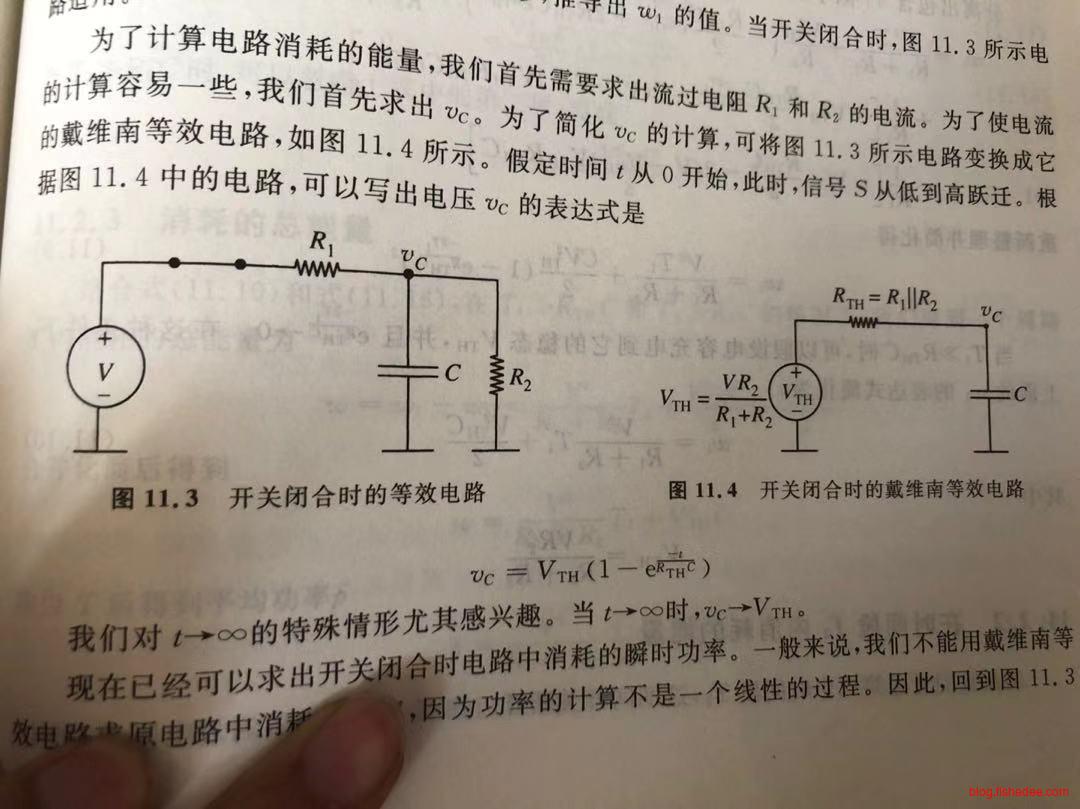
开关的闭合时,等效在右边的电路,电容充电。电容的电压显然为:
\[ v_C=V_{TH}(1-e^{\frac{-t}{R_{TH}C}}) \]
那么两个电阻的功率为:
\[ p(t) = \frac {(V-v_C)^2} {R_1} + \frac {v_C^2} {R_2} \]
那么,在T1时间段消耗的能量为:
\[ w_1=\int_{t=0}^{t=T_1} p(t)dt\\ \]
化简后,得到稳定时,为:
\[ w_1=\frac {V^2} {R_1+R_2} T_1 + \frac {V_{TH}^2C} {2} \]
12.1.2 T2时间段
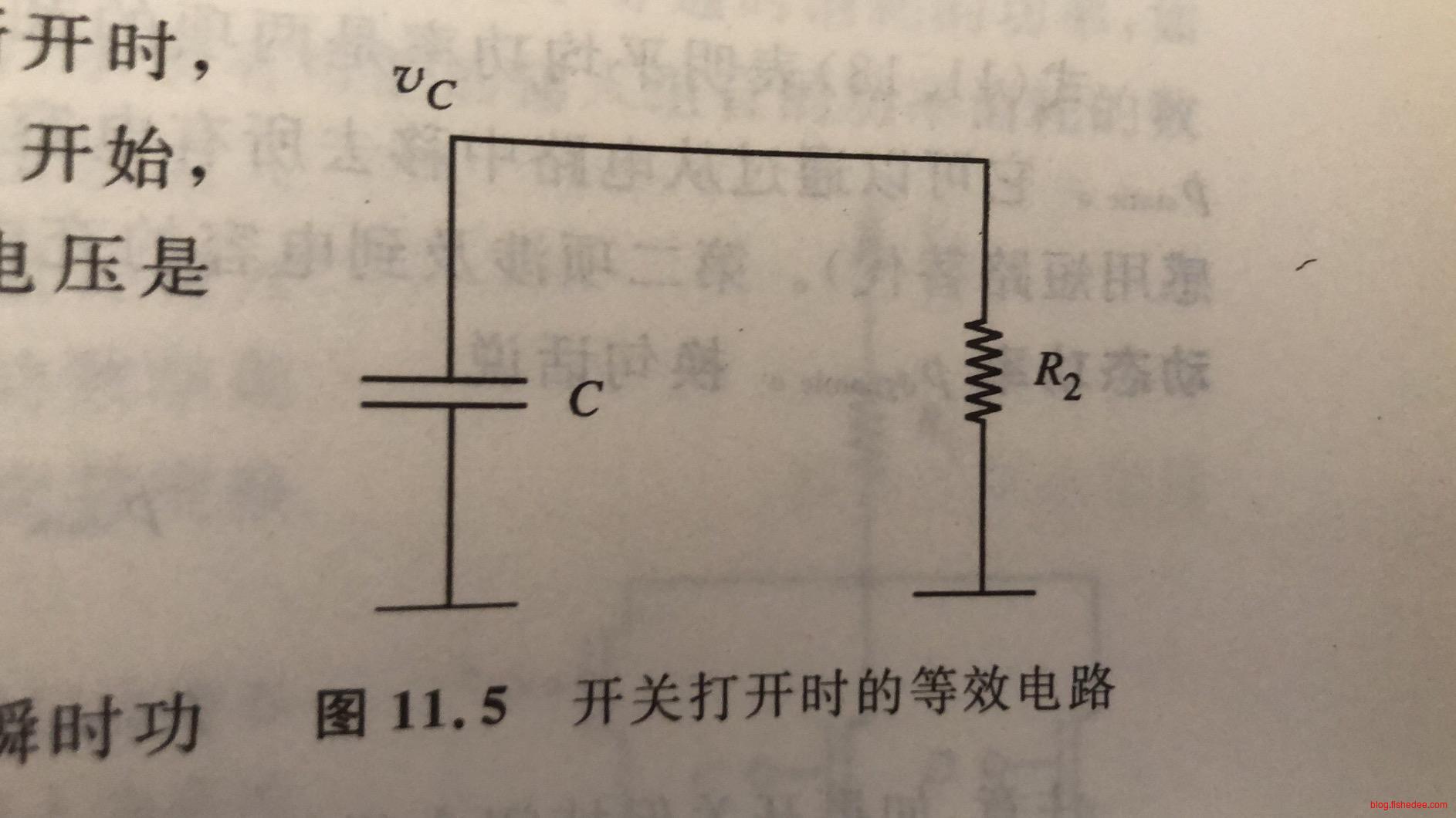
开关断开后,等效于上述的电路,电容放电。电容的电压显然为:
\[ v_C=v_{TH}e^{\frac {-t} {R_2C}} \]
所以,电阻2消耗的功率和能量为:
\[ p(t) = \frac {v_C^2} {R_2}\\ w_2 = \int_{t=0}^{t=T_2} p(t)dt\\ \]
化简后,得到稳定时,为:
\[ w_2 = \frac {V_{TH}^2C} {2} \]
12.1.3 总能量
总能量为:
\[ w = w_1+w_2=\frac {V^2} {R_1+R_2} T_1 +V_{TH}^2C \]
除以总时间为T,得到平均功率为:
\[ \overline{p} = \frac {w} {T} \\ = \frac {V^2} {R_1+R_2} \frac {T_1}{T} +\frac {V_{TH}^2C}{T}\\ = \frac {V^2} {2(R_1+R_2)} +\frac {V_{TH}^2C}{T}\\ \]
可以看出,功率分为两部分,第一部分与方波频率,电容,电感都无关,称为静态功率。第二部分取决于方波频率,电容,称为动态功率。
12.2 逻辑门的功率
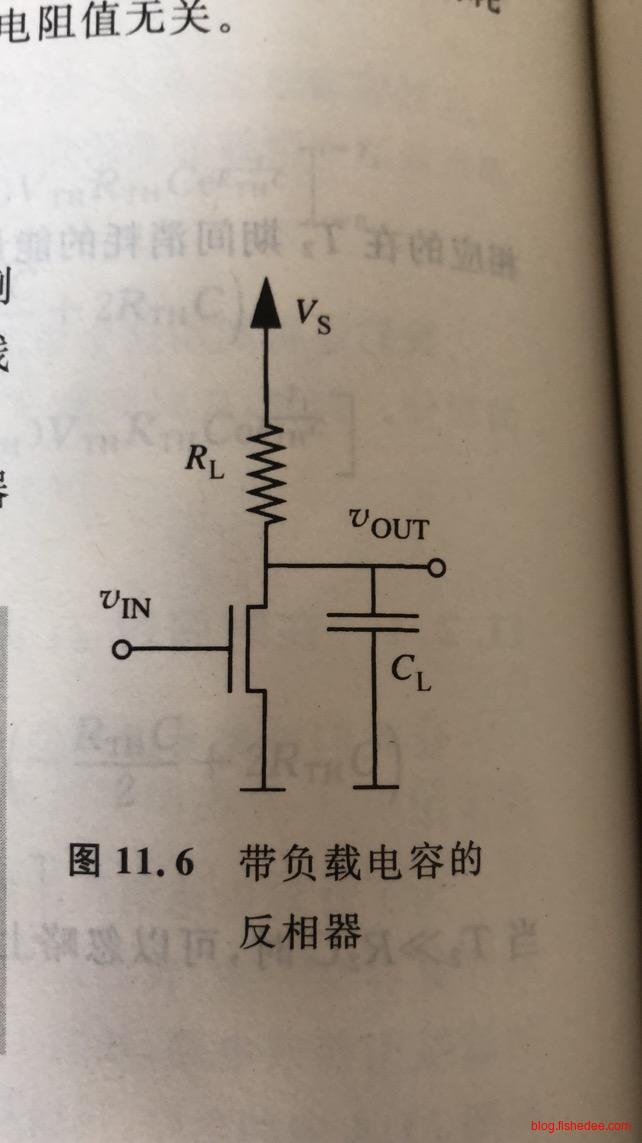
这是一个带负载电容的反相器,我们期望计算得到它的平均功率
12.2.1 T1阶段
开关闭合时,电容电压从\(V_s\)下降到\(V_{OH}\)
12.2.2 T2阶段
开关断开后,电容电压从\(V_{OH}\)上升到\(V_{s}\)
12.2.3 总能量
\[ \overline{p}_{static} = \frac {V_s^2}{2(R_L+R_{ON})}\\ \overline{p}_{dynamic} = \frac {V_s^2R_L^2C_L}{(R_L+R_{ON})^2T} \]
计算和上一节类似,我们得出了逻辑门的静态功率和动态功率,一般来说,逻辑门的静态功率远大于动态功率。
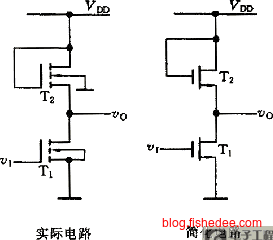
12.3 NMOS逻辑门
我们之前的逻辑门,上拉电阻一直是\(R_L\),但是大电阻的\(R_L\)并不好做。所以,NMOS逻辑门用了另外一个MOSFET元件来代替\(R_L\)。上拉的MOSFET栅极长度更长,所以它的\(R_{ON}\)更大,故而能满足静态原则,它的功率以计算依然可以使用12.2节的方法。
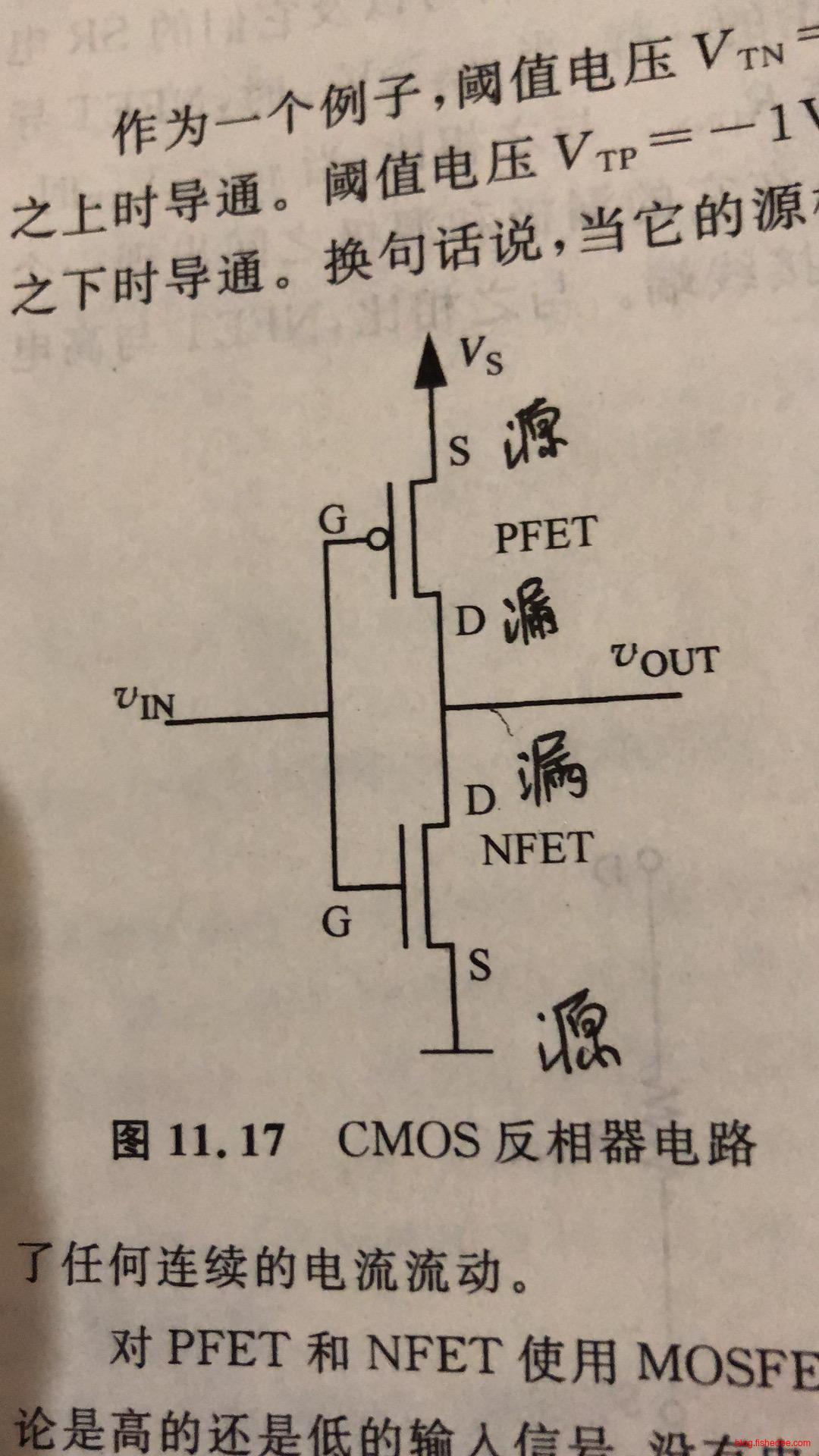
12.4 CMOS逻辑门
\[ p_{dynamic} = fV_s^2C_L \]
CMOS逻辑门,它不用上拉电阻,而是用PMNOS。PMNOS的导通逻辑,刚好与NMONS导通逻辑相反,低电平导通。所以,理论上CMOS逻辑门没有同时电源经电阻接地的情况,也就是没有静态功率,全部只有动态功率。所以,它的功率要比NMOS逻辑门要少很多!
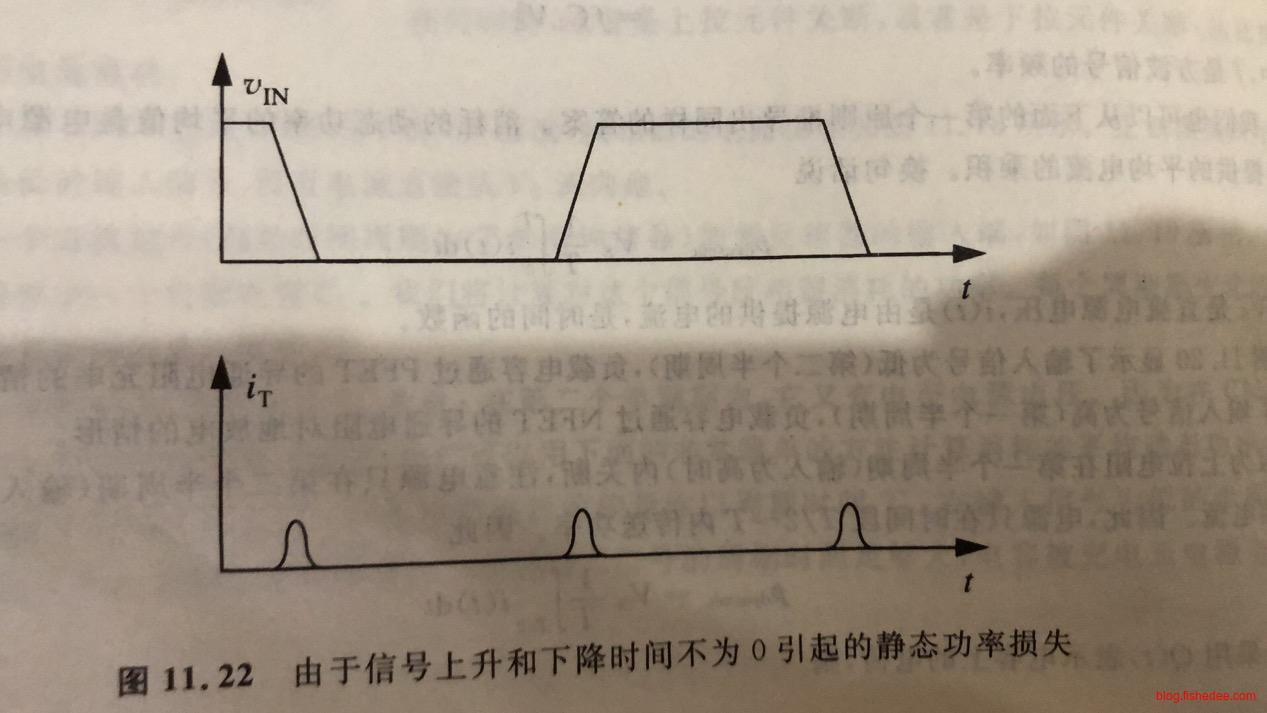
但是,实际上依然还有一点点的静态功率。因为上升和下降是需要时间的,中途的短暂时间里面,上下逻辑门会完全导通的,但是这个时间很多,静态功率依然很低。CMOS逻辑门的总体功率大概是NMOS逻辑门功率的十分之一。
13 二阶电路的暂态过程
分析二阶电路的方法和一阶电路方法相差不大,但是会涉及到复数根的处理的问题,要提前看附录。
13.1 复数与三角函数
13.1.1 实数域下的自然指数函数
\[ f(x) = e^{x}\\ f'(x) = e^{x}\\ \int f(x) = e^{x}\\ \]
我们都知道这是一个指数函数,它的输入是一个实数。这个函数的特别之处在于,它的导数与积分都是它自己,所以这个函数在求微分方程时经常会出现。
\[ \frac {d^2f(x)} {dx^2}+\frac{f(x)}{C} = 0 \]
当我们遇到这个微分方程,我们就尝试用这个指数函数去套它,看能不能成功\(f(x) = Ae^{kx}\),代入得到
\[ Ak^2e^{kx}+\frac {Ae^{kx}} {C} = 0\\ k^2+\frac {1} {C} = 0\\ \]
那么,当C是一个负数的时候,这个方程就有解,我们的猜测就是对的,这个时候,方程的解为:
\[ k_1 = \sqrt {-\frac {1}{C}}\\ f(x) = A_1e^{k_1x}\\ k_2 = -\sqrt {-\frac {1}{C}}\\ f(x) = A_2e^{k_2x} \]
由于方程有两个解,这两个解都是结果,所以总的结果为:
\[ k_1 = \sqrt {-\frac {1}{C}}\\ k_2 = -\sqrt {-\frac {1}{C}}\\ f(x) = A_1e^{k_1x}+A_2e^{k_2x}\\ \]
13.1.2 实数域下的三角函数
\[ sin'(x) = cos(x)\\ cos'(x) = -sin(x) \]
但是,对于三角函数而言,它的两次求导以后就是自己本身,拥有了和\(e^{x}\)类似的能力,所以,对于微分方程
\[ \frac {d^2f(x)} {dx^2}+\frac {f(x)} {C} = 0 \]
我们不仅要考虑指数函数能否合适,三角函数\(f(x)=A_1sin(\omega x)+A_2cos(\omega x)\),也有可能合适呀。我们代入试试:
\[ -A_1C\omega^2sin(\omega x)-A_2C\omega^2cos(\omega x)+A_1sin(\omega x)+A_2cos(\omega x) = 0\\ \begin{cases} A_1-A_1C\omega^2=0\\ A_2-A_2C\omega^2=0\\ \end{cases}\\ \omega = \sqrt{\frac{1} {C}} \]
可以看出,当C是正数的时候,这个微分方程就有解,这个时候,方程的解为:
\[ \omega = \sqrt{\frac{1} {C}}\\ f(x) = A_1sin(\omega x)+A_2cos(\omega x) \]
13.1.3 实数域下的指数线性组合函数
我们经过以上讨论,当C值在正数或负数时,都有不同的解形式。那么,当C值是0的时候呢?
\[ f(x) = A_1e^{kx}+A_2xe^{kx} \]
可以证明,当C值为零的时候,为上述形式的方程
13.1.4 复数域下的指数函数
我们知道对于不同的C值,解有不同的形式。但是当我们去扩展指数函数,让它的定义域是复数的时候,再配合欧拉公式,我们能得到一样的结果。
\[ Ak^2e^{kx}+\frac {Ae^{kx}} {C} = 0\\ k^2+\frac {1} {C} = 0\\ \]
当C值为正数的时候,上述方程为复数根,为
\[ \omega_0 = \sqrt{\frac {1}{C}}\\ k_1=+j\omega_0\\ k_2=-j\omega_0\\ f(x) = A_1e^{k_1x}+A_2e^{k_2x}\\ = A_1e^{+j\omega_0 x}+A_2e^{-j\omega_0 x} \]
根据欧拉公式\(e^{j\omega t} = cos(\omega t)+jsin(\omega t)\),代入后得到
\[ f(x) = A_1[cos(\omega t +j sin(\omega t)]+A_2[cos(\omega t) -j sin(\omega t)]\\ f(x) = (A_1+A_2)cos(\omega t)+(A_1-A_2)jsin(\omega t) \]
虽然,这个函数是依然带有复数的,但是我们在求根的时候用了复数根,这里换回到实数方程的时候,我们就不加证明地认为,实际方程的解就是:
\[ f(x) = (A_1+A_2)cos(\omega t)+(A_1-A_2)sin(\omega t) \]
一个不含j的实数域上的三角函数
13.1.5 验证
\[ \frac {d^2f(x)} {dx^2}+\frac {f(x)} {C} = 0 \]
我们来验证一下,用两种方法最后求出的结果是不是一样,对于以上的微分方程,我们已知\(f(0)\)和\(f'(0)\),求方程,最开始用传统的三角函数,猜想解的形式为:
\[ \omega = \sqrt{\frac{1} {C}}\\ f(x) = A_1sin(\omega x)+A_2cos(\omega x) \]
然后,我们代入求\(A_1\)和\(A_2\),得到:
\[ f(0) = A_2\\ f'(0) = A_1\omega cos(\omega x)-A_2\omega sin(\omega x)=A_1\omega\\ \]
所以,总方程为:
\[ \omega = \sqrt{\frac{1} {C}}\\ f(x) = \frac {f'(0)}{\omega}sin(\omega x)+f(0)cos(\omega x) \]
然后,另外,我们用复指数方程,来求解,猜想解的形式为
\[ \omega = \sqrt{\frac{1} {C}}\\ f(x) = B_1 e^{+j\omega x}+B_2e^{-j\omega x} \]
代入求\(B_1\)和\(B_2\),得到:
\[ \begin{cases} f(0)=B_1+B_2\\ f'(0)=B_1\omega-B_2\omega\\ \end{cases}\\ \begin{cases} B_1=\frac {f(0)+\frac{f'(0)}{\omega}}{2}\\ B_2=\frac {f(0)-\frac{f'(0)}{\omega}}{2}\\ \end{cases} \]
因此,我们得到了复指数方程。我们代入到13.1.4节的推论,验证一下结果。
\[ B_1+B_2=f(0)=A_1\\ B_1-B_2=\frac{f'(0)} {\omega}=A_2\\ \]
完美,复指数方程得出的结果系数与三角函数方程得到的结果系数一致。
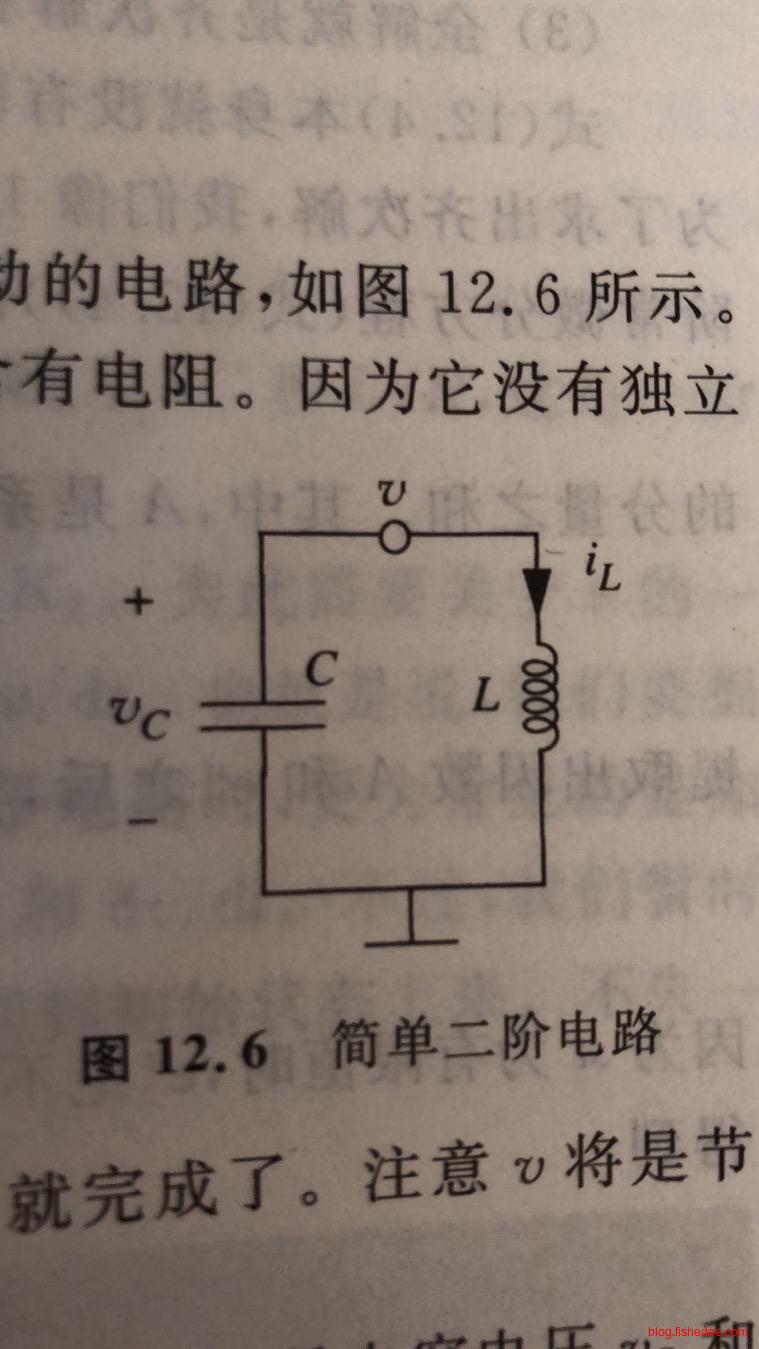
13.2 无驱动的LC电路
我们来研究同时有电容和电感,但是没有电阻的电路,称为LC电路。我们有:
\[ C\frac {dv} {dt} + \frac {1}{L} \int_{-\infty}^{t} v(t)dt = 0\\ \frac {d^2v}{dt^2} + \frac {1} {LC} v(t) = 0 \]
对于这个二阶的齐次微分方程,我们依然猜测解形式为\(v(t) = Ae^{st}\),代入后得到
\[ As^2e^{st} + \frac {1}{LC}Ae^{st} = 0\\ s^2+\frac {1} {LC} = 0\\ \]
这个时候,s显然是一个复数根,它的两个根为:
\[ s_1=+j\omega_0\\ s_2=-j\omega_0\\ w_0=\sqrt{\frac {1} {LC}} \]
显然,因为是两个复数根,所以这是一个解应该是三角函数的形式,设解为\(v(t)=K_1cos(\omega_0 t)+K_2 sin(\omega_0 t)\),然后我们根据初始条件\(v(0)\)与\(v'(0)\)来求解\(K_1\)和\(K_2\)。
\[ v(0) = K_1\\ v'(0) = \omega_0K_2\\ \]
但是,\(v(0)\)与\(v'(0)\)并不是我们常见的电路初始状态,电路的初始状态应该是\(v_C(0)\)和\(i_L(0)\),我们继续推导一下:
\[ v(0) = v_C(0)\\ Cv'(0) = C\frac{dv(t)}{dt} = -i_L(0) \]
因此,整理一下,我们得到最终的结果为:
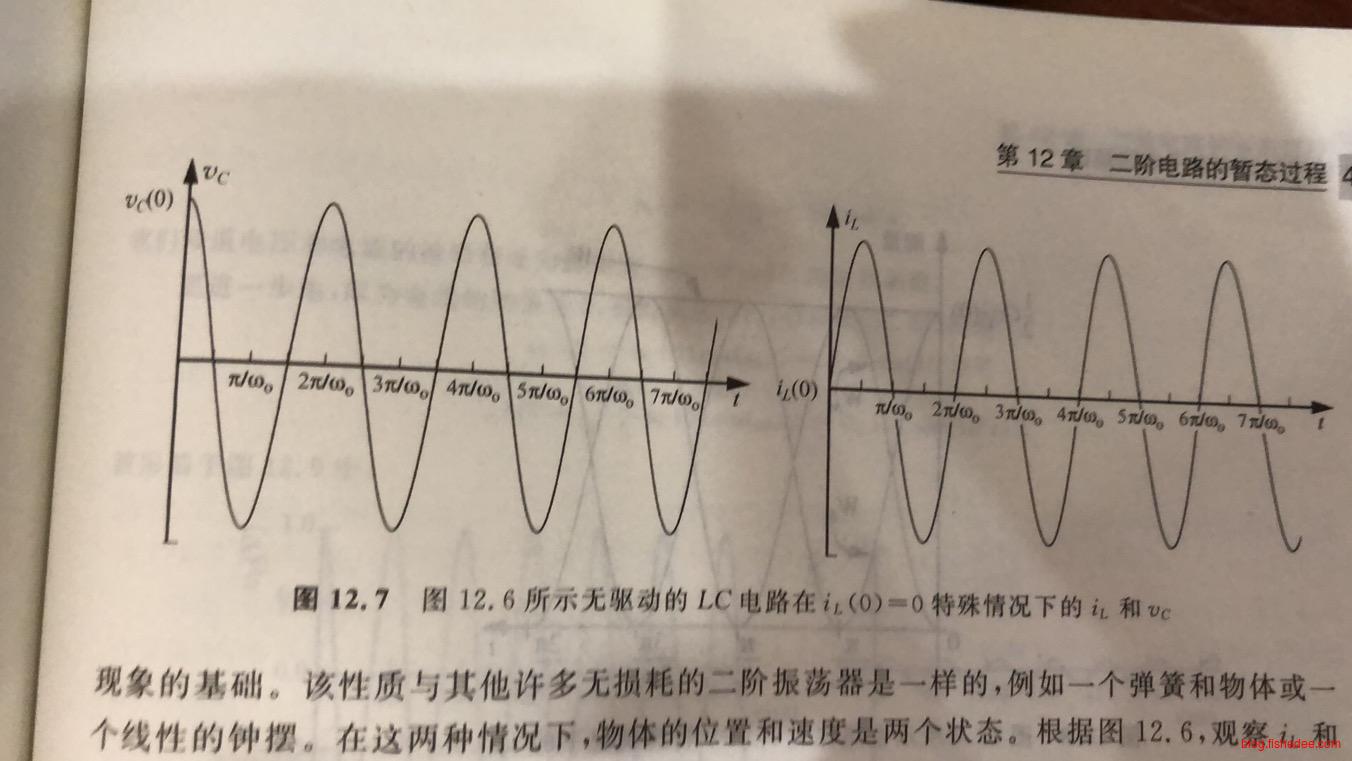
\[ \omega_0 = \sqrt {\frac {1} {LC}}\\ v(t) = v_C(0)cos(\omega_0 t)-\sqrt {\frac{L} {C}}i_L(0)sin(\omega_0 t) \]
可以看出,电容和电感是在相互震荡的图形,能量在两个元件之间不断交换。
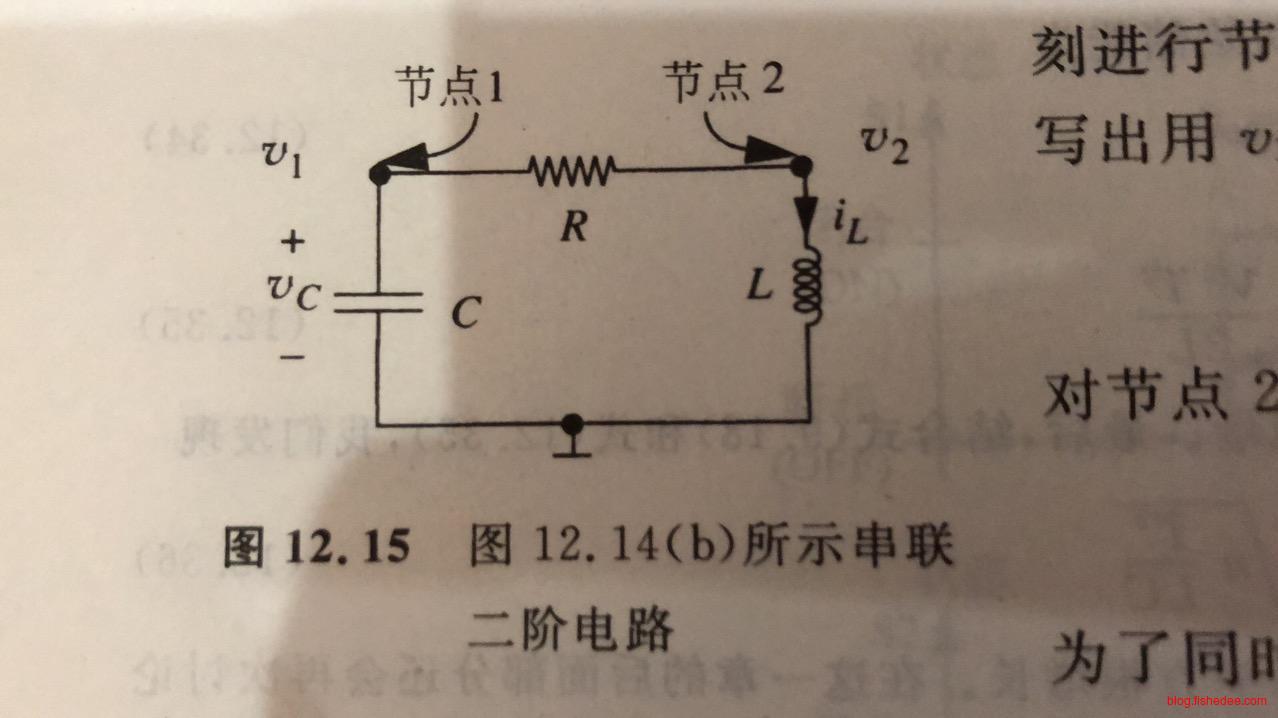
13.3 无驱动的串联RLC电路
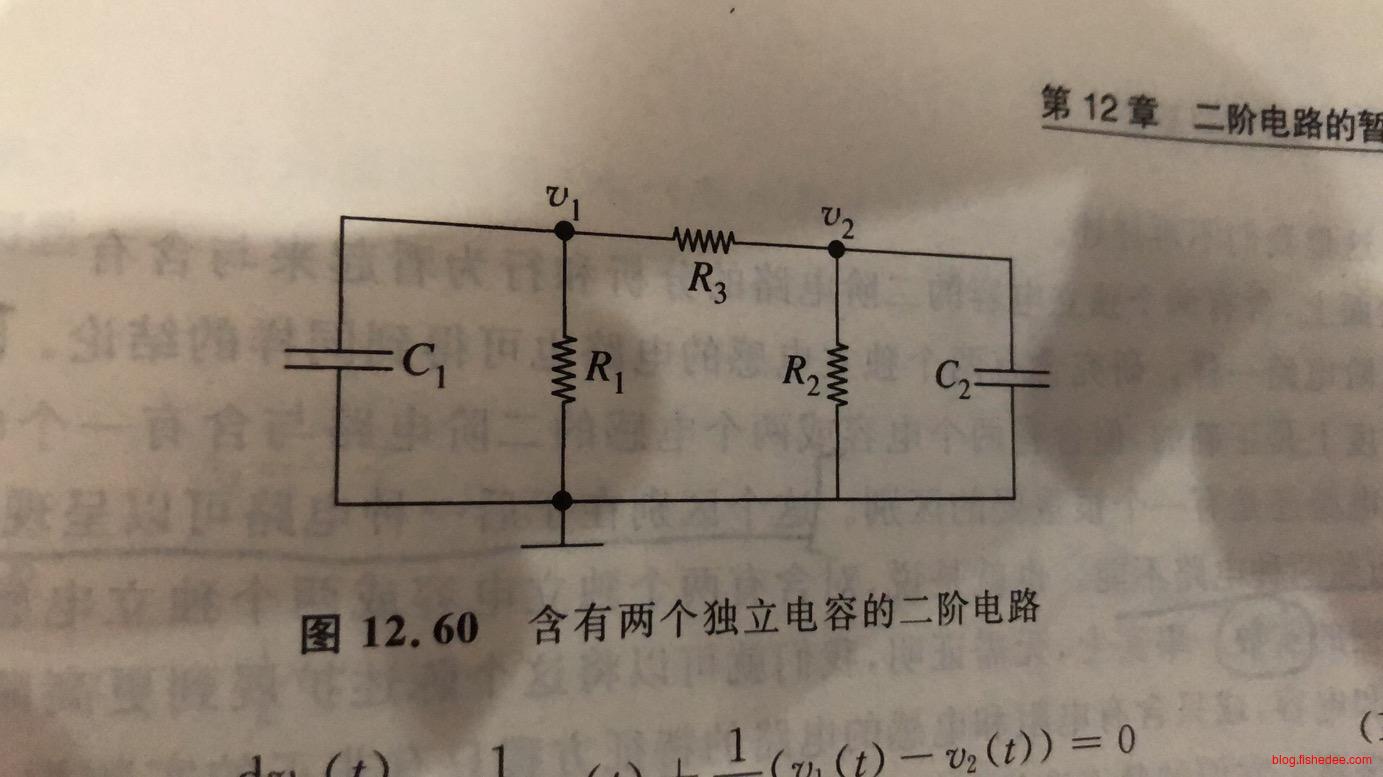
我们进一步研究无驱动的串联RLC电路,依然是列出微分方程
\[ C\frac {dv_1(t)} {dt} + \frac {v_1(t)-v_2(t)} {R} = 0\\ \frac {v_2(t)-v_1(t)}{R} + \frac {1}{L}\int_{-\infty}^{t} v_2(t)dt =0\\ 化简后得到 \frac {d^2v_1(t)} {dt^2}+\frac {R}{L}\frac{dv_1(t)} {dt}+\frac{1}{LC}v_1(t)=0 \]
这是二阶微分方程,代入复指数形式为\(Ae^{st}\),后得到
\[ \alpha = \frac {R} {2L}\\ \omega_0=\frac {1} {\sqrt{LC}}\\ s_1=-\alpha+\sqrt{\alpha^2-\omega_0^2}\\ s_2=-\alpha-\sqrt{\alpha^2-\omega_0^2}\\ v_1(t)=A_1e^{s_1t}+A_2e^{s_2t} \]
然后根据初始状态,\(v_C(0)\)和\(i_L(0)\),求得\(A_1\)和\(A_2\),最终结果为:
\[ v_C(t)=\frac {Cs_2v_C(0)+i_L(0)} {C(s_2-s_1)} e^{s_1t}+\frac {Cs_1v_C(0)+i_L(0)}{C(s_1-s_2)}e^{s_2t}\\ i_L(t) = -s_1\frac{Cs_2v_C(0)+i_L(0)}{s_2-s_1} e^{s_1t}-s_2\frac{Cs_1v_C(0)+i_L(0)}{s_1-s_2}e^{s_2t} \]
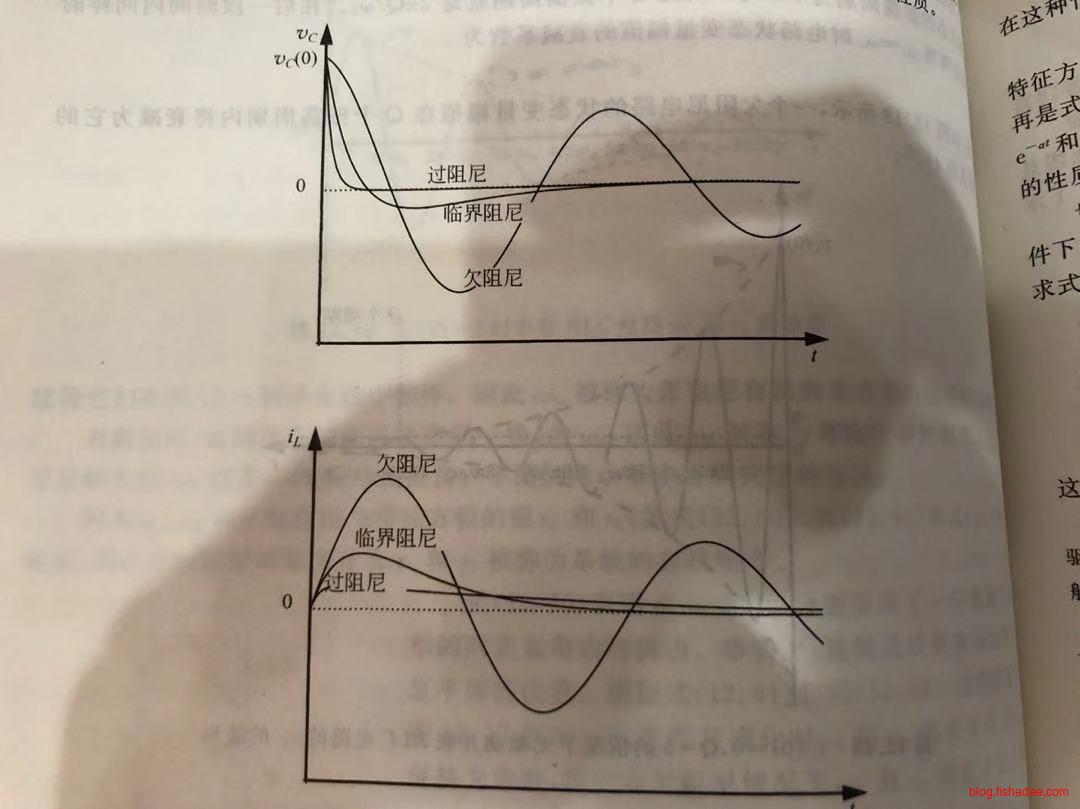
13.3.1 欠阻尼
\[ \omega_d=\sqrt{\omega^2-\alpha^2} \]
当\(\alpha<\omega_0\)的时候,上述的\(s_1\)和\(s_2\)都是复数形式,也就是方程的解应该是一个三角函数。
从解中可以看出,电容和电感在互相震荡,但是由于\(e^{-\alpha t}\)的作用,它们震荡的幅度在不断减少。我们定义\(\omega_0\)为无阻尼自然频率,\(\omega_d\)为有阻尼自然频率。
\[ Q=\frac {\omega_0}{2\alpha} \]
我们定义一个RLC电路的Q值。从Q值中可以看出,Q值越大的时候,震荡时间就越长,Q值越小的时候,震荡时间就越短。
\[ t = Q\frac {2\pi}{\omega_d}\\ e^{-\alpha t} \approx e^{-\pi} = 0.04\\ \]
另外,从推导中可以看出,当Q个周期以后,震荡的幅度已经接近于零。
13.3.2 过阻尼
当\(\alpha > \omega_0\)的时候,上述的\(s_1\)和\(s_2\)都是两个不同的实数,也就是方程的解就是一个实指数形式。
可以看出,图像就是一条,直接指数趋向于零的图形。
当电阻很大的时候,我们甚至可以认为,串联RLC电路,是由独立RL电路,和独立RC电路组成的。
13.3.3 临界阻尼
当\(\alpha = \omega_0\)的时候,上述的\(s_1\)和\(s_2\)都是两个不同的实数,也就是方程的解就是\(A_1e^{st}+A_2te^{st}\)的形式
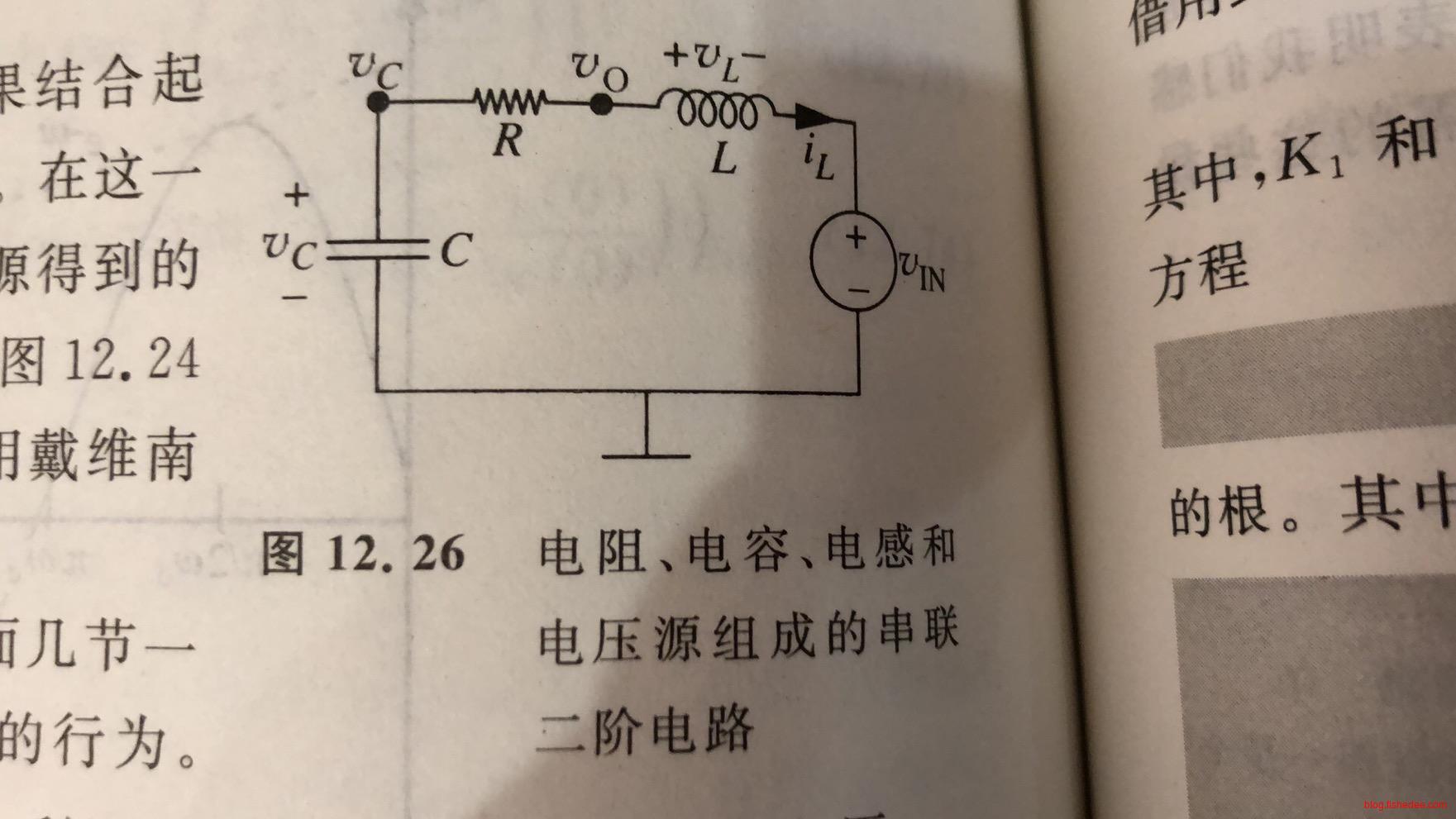
13.4 有驱动的串联RLC电路
我们在串联RLC电路加入了电源,组成了有驱动的串联RLC电路。我们依然列微分方程
\[ C\frac {dv_C(t)} {dt} + \frac {v_C(t)-v_O(t)} {R} = 0\\ \frac {v_O(t)-v_C(t)}{R} + \frac {1}{L}\int_{-\infty}^{t} (v_O(t)-v_{IN}(t))dt =0\\ 化简后得到 \frac {d^2v_C(t)} {dt^2}+\frac {R}{L}\frac{dv_C(t)} {dt}+\frac{1}{LC}v_C(t)=\frac {1} {LC}v_{IN}(t) \]
这依然是一个二阶微分方程,跟以前不同的是,这是一个非齐次的二阶微分方程。没事,我们先解出对应的齐次解二阶微分方程。
\[ \alpha = \frac {R} {2L}\\ \omega_0=\frac {1} {\sqrt{LC}}\\ s_1=-\alpha+\sqrt{\alpha^2-\omega_0^2}\\ s_2=-\alpha-\sqrt{\alpha^2-\omega_0^2}\\ v_C(t)=A_1e^{s_1t}+A_2e^{s_2t} \]
和之前的结果类型,依然分为过阻尼,欠阻尼,临界阻尼的三种情况。我们只讨论过阻尼的情况,也就是\(\alpha < \omega_0\)的情况。
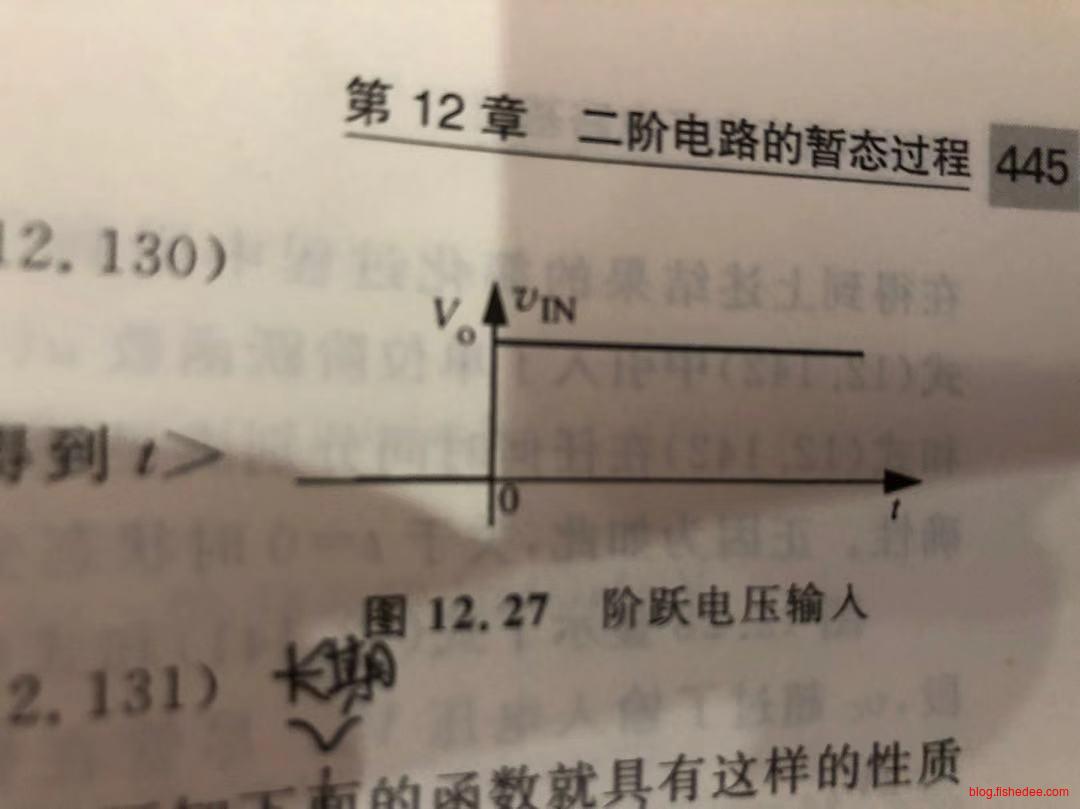
13.4.1 阶跃输入
当输入是阶跃输入电压源的时候,方程变为
\[ \frac {d^2v_C(t)} {dt^2}+\frac {R}{L}\frac{dv_C(t)} {dt}+\frac{1}{LC}v_C(t)=\frac {1} {LC}V_0 \]
显然,一个特解就是\(V_0\),那么全解就是
\[ v_C(t)=A_1e^{s_1t}+A_2e^{s_2t}+V_0 \]
然后,代入初始条件就能求出\(A_1\)和\(A_2\)了,轻松解决。
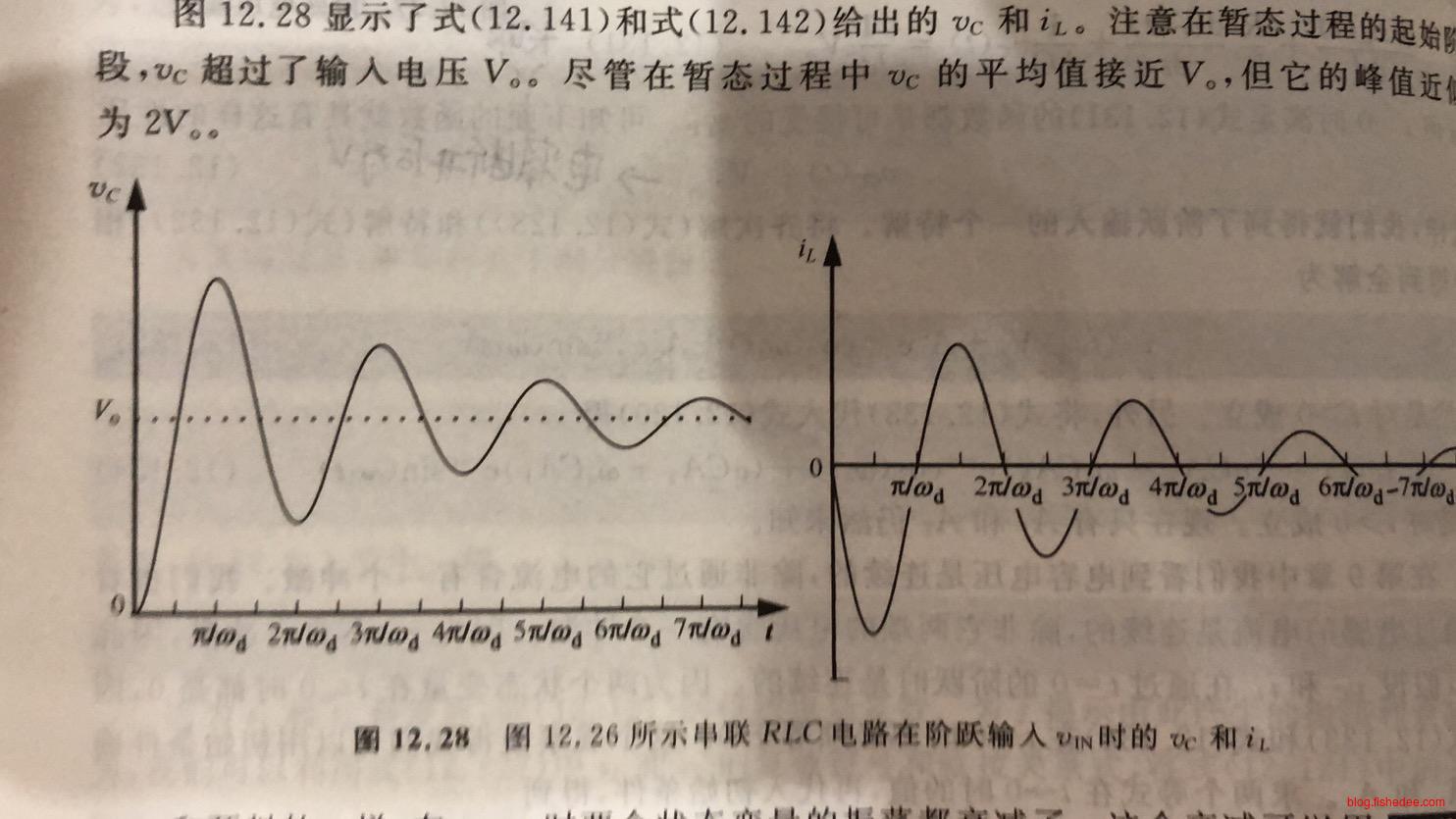
这是当初始状态为0,初始输入为阶跃电压源的结果,注意,电容的电压有段时间超过了\(V_0\)。
13.4.2 冲激输入
当输入是冲激输入的电压源的时候,我们做一个巧妙的类比。当冲激输入的一瞬间,相当于将所有电压源放到了电感两端。因为电感短期是开路的,电容短期是短路的。
\[ i_L(0) = - \frac {A} {L}\\ v_C(0) = 0\\ \]
因此,原电路相当于,初始状态为以上的条件的无驱动RLC电路。
13.5 两个电容或两个电感的电路
如果电路是双电容,或者双电感的时候,我们一样可以列微分方程来解决这个问题。但是,这个微分方程的特点是,它的复指数方程总是有两个不同的实数,所以,电路总是展示为过阻尼状态。而没有像RLC状态一样,出现震荡的情形。
13.6 MOSFET元件
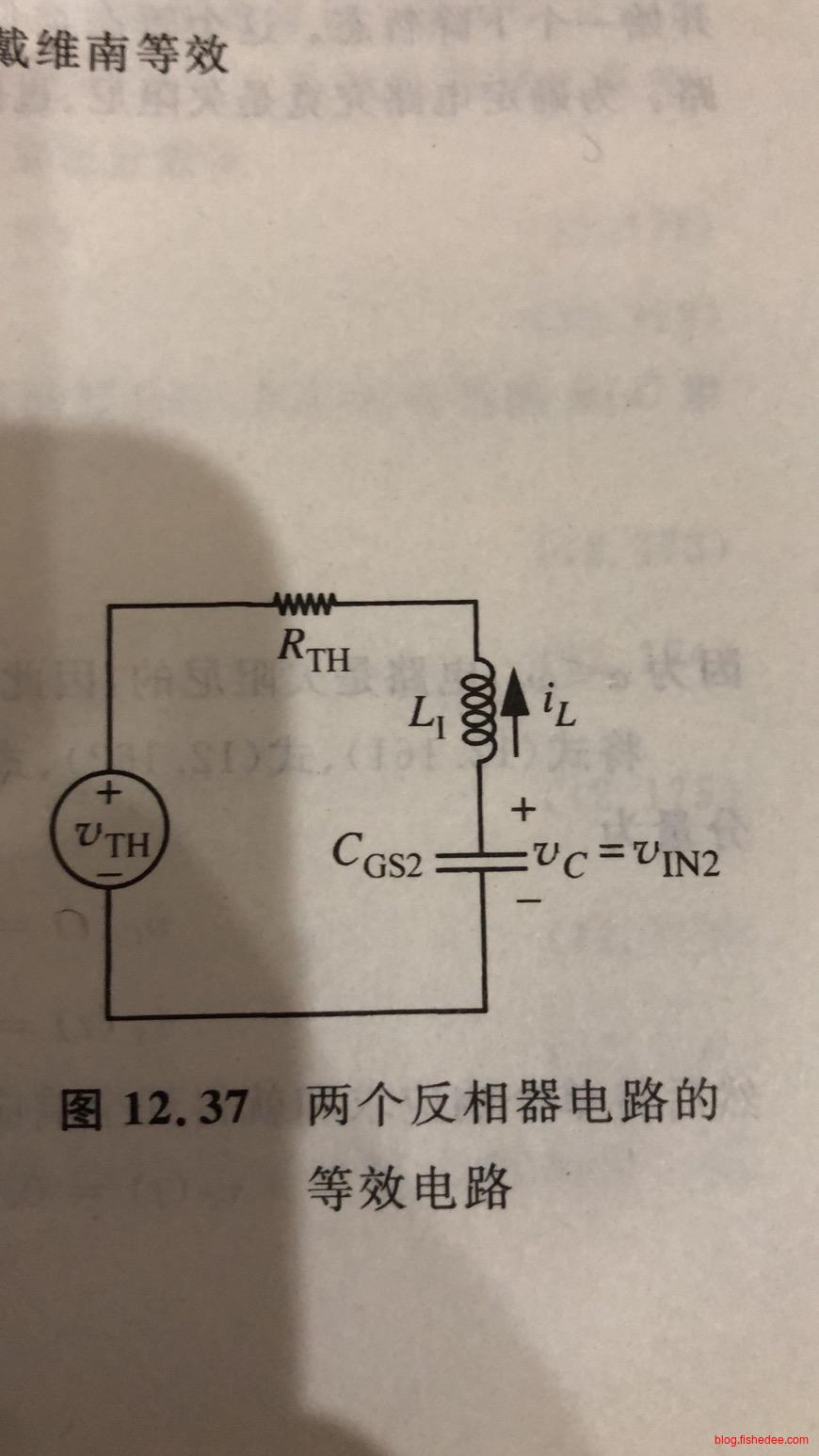
这次,我们将MOSFET元件在SRC模型上再推进一步,加入了实际可能的电感。
当MOSFET输出高电平的等效电路
当MOSFET输出低电平的等效电路
而等效电路的输出端,总是串联了一个电感和电容,而输出的电平就是电容两端的电压\(C_{GS2}\)。我们可以看出,整个电路的变化实际上就是一个串联RLC模型。
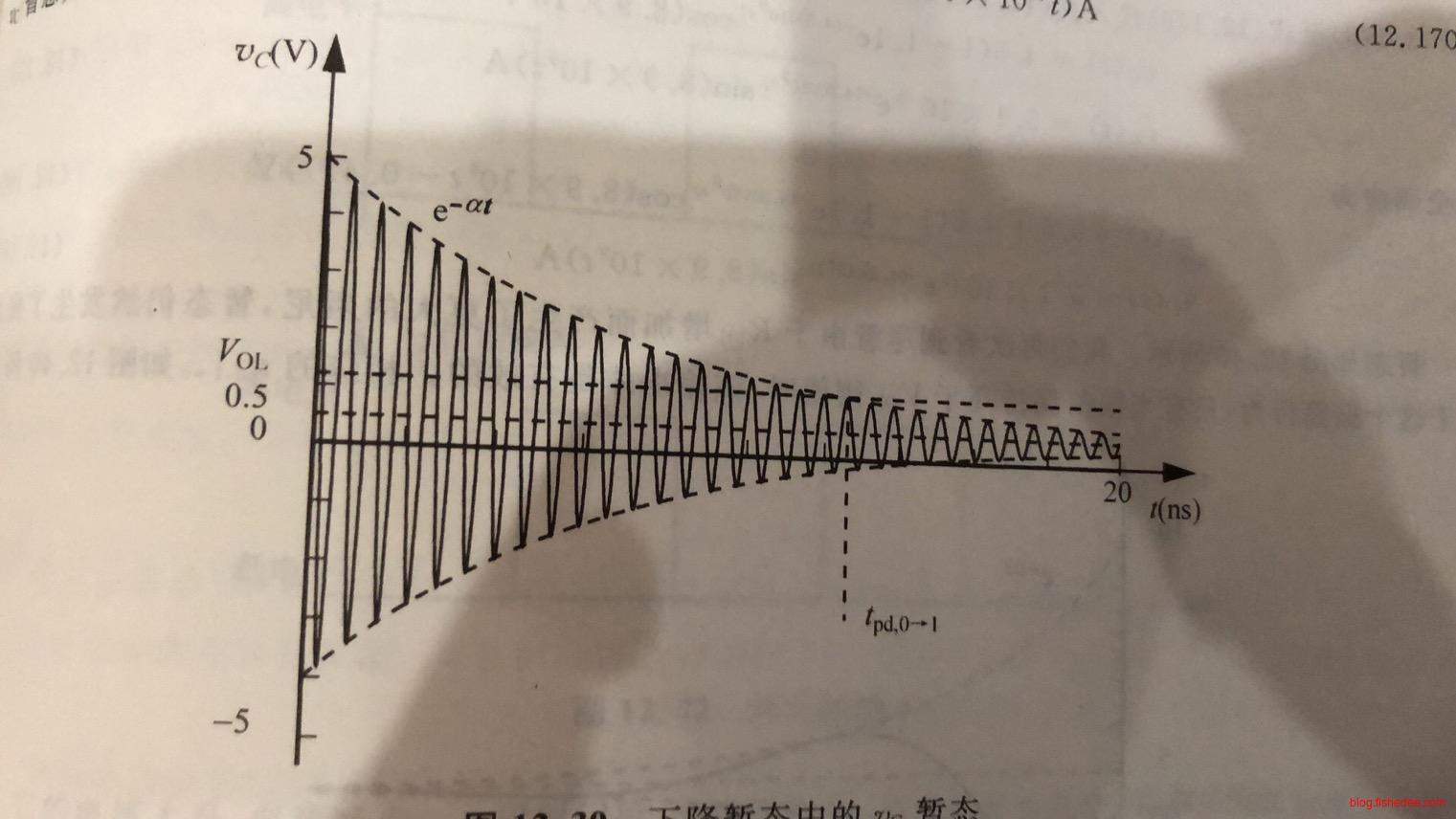
13.6.1 下降时间
下降时间,就是从5V下降到\(V_{OL}\)的时间。注意,这相当于电容初始状态为\(5V\),使用b图下的等效电路的结果。
当整个震荡幅度都低于\(V_{OL}\)时,才算是有效的输出低电平。
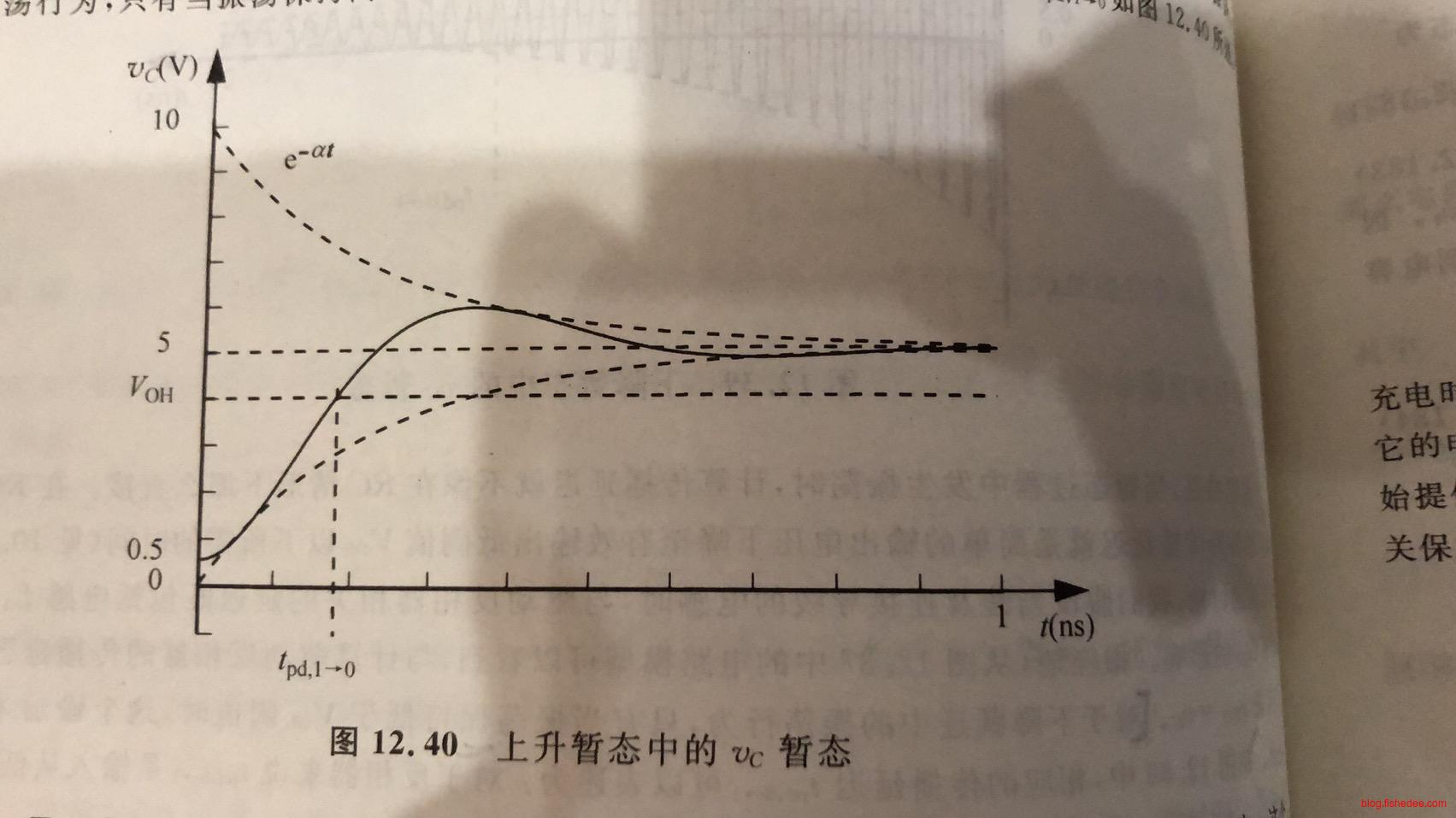
13.6.2 上升时间
上升时间,就是从0.5V上升到\(V_{OH}\)的时间。注意,这相当于电容初始状态为\(0.5V\),使用a图下的等效电路的结果。
当整个震荡幅度都高于\(V_{OH}\)时,才算是有效的输出高电平。
- 本文作者: fishedee
- 版权声明: 本博客所有文章均采用 CC BY-NC-SA 3.0 CN 许可协议,转载必须注明出处!